| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2002 год
Важнейшие научные достижения 2002 года
- Важнейшие научные достижения 2002 года
- Адаптивный метод конечных элементов для стационарной и нестационарной задач Навье — Стокса вязкой несжимаемой жидкости
- Моделирование процессов лазерного охлаждения и удержания атомов
- Применение нанопорошков химических соединений для повышения качества металлоизделий
- Моделирование нелинейных деформаций оболочек
- Федеральная целевая научно-техническая программа "Исследования и разработки по приоритетным направлениям развития науки и техники гражданского назначения"
- Федеральная целевая программа "Государственная поддержка интеграции высшего образования и фундаментальной науки"
- Федеральная целевая программа "Мировой океан"
Адаптивный метод конечных элементов для стационарной и нестационарной задач Навье — Стокса вязкой несжимаемой жидкости
Номер научного направления ОИВТА:
2
Авторы научного результата:
Шайдуров В. В., директор ИВМ СО РАН, член-корреспондент РАН;
Киреев И. В., н.с., к.ф.-м.н.;
Пятаев С. Ф., ученый секретарь ИВМ СО РАН, к.ф.-м.н.;
Карепова Е. Д., н.с., к.ф.-м.н.;
Гилева Л. В., н.с., к.ф.-м.н.
e-mail
Аннотация. Для стационарной и нестационарной двумерных задач Навье — Стокса вязкой несжимаемой жидкости методом конечных элементов построены устойчивые вариационно — разностные схемы с использованием простых конечных элементов: билинейных внутри области и линейных вблизи криволинейной границы для скоростей и кусочно-постоянных для давления с вычислительной фильтрацией. Предложены приемы построения весовых оценок погрешности функционалов приближенного решения, позволяющие локальную апостериорную адаптацию триангуляции в методе конечных элементов с целью оптимизации размеров ячеек для повышения точности, как для стационарной, так и нестационарной задачи. На основе этих оценок разработаны алгоритмы повышения порядка точности приближенного решения вблизи криволинейной границы, а затем в целом по области на основе экстраполяции Ричардсона.
:
- Быкова Е. Г., Калпуш Т. В., Карепова Е. Д. и др.
Уточненные численные методы для задач конвекции — диффузии. Том 1 (на англ. яз.). — Новосибирск: ИМ СО РАН. — 2001. — 252 с. - Быкова Е. Г., Гилева Л. В., Киреев И. В. и др.
Уточненные численные методы для задач конвекции — диффузии. Том 2 (на англ. яз.). — Новосибирск: ИМ СО РАН. — 2002. — 178 с.
| К началу | |
Моделирование процессов лазерного охлаждения и удержания атомов
Номер научного направления ОИВТА:
2
Авторы научного результата:
Краснов И. В., в.н.с, д.ф.-м.н., тел.
Полютов С. П., м.н.с., e-mail: psp@icm.krasn.ru
Аннотация Разработаны математические модели, описывающие механическое действие интерферирующих оптических полей произвольной трехмерной конфигурации на движение резонансных атомов. На основании этих моделей найдены трехмерные симметричные конфигурации слабых бигармонических полей, при которых атомы совершают финитное движение в ячейках эффективной световой решетки с периодом, превышающим длину волны света. При этом показана возможность долговременного удержания резонансных атомов в трехмерных сверхглубоких потенциальных ямах, индуцированных бихроматическими лазерными пучками малой интенсивности и определены достаточные условия полного преодоления ограничений на устойчивую локализацию, вытекающих из оптической теоремы Ирншоу. Полученные теоретические результаты дают эффективный метод решения важной проблемы построения диссипативных, чисто оптических (без использования магнитного поля) ловушек для большой группы атомов типа четно-четных изотопов иттербия и щелочноземельных элементов и могут быть использованы для постановки новых фундаментальных экспериментов с холодными частицами подобного типа.
:
- Гаврилюк С. А., Краснов И. В., Полютов С. П.
Трехмерные интерферен-ционные эффекты в механическом действии слабых бигармонических полей на частицы с квантовым переходом J=0>J=1 // ЖЭТФ. — 2001. — Т. 120. — Вып. 5(11) — С.1135–114 9. - Краснов И. В., Полютов С. П.
Удержание атомов с невырожденным основным состоянием в трехмерной диссипативной оптической сверхрешетке // Письма в ЖЭТФ. — 2002. — Т. 76. — Вып. 5. — С. 328–332 . - Krasnov I. V., Polyutov S. P.
All optical atom trap for Ytterbium and Alkaline-Earth Isotopes // Proc. the 6-th Int. Symp. on Laser Physics and Laser Technology. -Harbin, China. — 2002. — Р. 32-36. - Krasnov I. V., Polyutov S. P.
The superlattice of the moving atoms induced by bichromatic laser field // Proc. the 6-th Int. Symp. on Laser Physics and Laser Technology. -Harbin, China. — 2002. — Р. 42-36.
| К началу | |
Применение нанопорошков химических соединений для повышения качества металлоизделий
Номер научного направления ОИВТА:
2
Автор научного результата:
Крушенко Г. Г., главный научный сотрудник отдела машиноведения, д.т.н., профессор, тел.
Аннотация. Разработаны промышленные технологии применения ультрадисперсных порошков (нанопорошков) высокопрочных тугоплавких химических соединений (нитриды, карбонитриды, бориды, оксиды) с размерами частиц до 100 нм, получаемых плазмохимическим синтезом и взрывным методом, для повышения физико-механических характеристик и качества металлоизделий, изготовляемых разными способами из алюминиевых деформируемых и литейных сплавов, сталей, серого и износостойкого чугуна. Разработанные технологические процессы нашли применение в литейном производстве, в металлургии, обработке металлов давлением и сварочном производстве как при получении заготовок (литье слитков), так и при изготовлении конечной продукции в виде деталей машин и механизмов. С использованием нанопорошков разработана технология изготовления многоцелевого алюминиевого композита с волокнистой структурой, обладающего повышенными характеристиками механических свойств и демпфирующей способности. Разработки защищены 22 авторскими свидетельствами и патентами на изобретения.
:
- Крушенко Г. Г.
Нанопорошки химических соединений — средство повышения качества металлоизделий и конструкционной прочности // Заводская лаборатория. Диагностика материалов. ( 1999. ( № 11. ( С. 42-50. - Крушенко Г. Г.
Противопригарные покрытия, содержащие нанопорошки химических соединений // Литейное производство. ( 2002. ( № 2. (С. 13-14. - Крушенко Г. Г.
Применение нанопорошков химических соединений для улучшения качества металлоизделий // Технология машиностроения. ( 2002. ( № 3. ( С. 39-40. - Трещиностойкость и механические свойства конструкционных материалов технических систем / В. В. Москвичев, Н. А. Махутов, Г. Г. Крушенко и др.
— Новосибирск: Наука. — 2002. — 334 с.
| К началу | |
Моделирование нелинейных деформаций оболочек
Номер научного направления ОИВТА:
2
Автор научного результата:
Шкутин Л. И., в.н.с., д.ф.-м.н., тел.
Аннотация. На основе коротационной формулировки уравнений механики деформируемого твердого тела построена новая нелинейная модель деформирования оболочек, вводящая независимые поля конечных перемещений, конечных поворотов и поперечных деформаций. В рамках сформулированной модели получены новые разветвленные решения нелинейных задач квазистатического деформирования пластин и оболочек при больших перемещениях и поворотах. Практическая значимость результатов заключается в возможности более глубокого анализа нелинейных процессов деформирования оболочечных конструкций с оценкой параметров их катастрофического поведения.
Цилиндрическая панель под действием гравитационной нагрузки
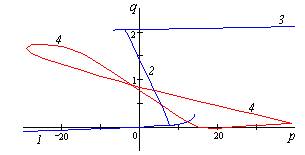
Фазовые кривые равновесных состояний: p — параметр нагрузки, q — относительное перемещение
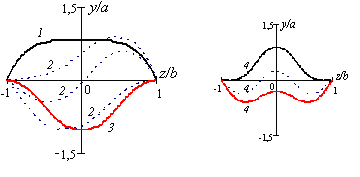
Моды изгиба, соответствующие ветвям 1, 2, 3, 4
:
- Шкутин Л. И.
Инкрементальная модель деформации оболочки // Прикл. механика и техн. физика. — 1999. — Т. 41. — № 5. — С. 202–207 . - Шкутин Л. И.
Численный анализ разветвленных форм изгиба арок // Прикл. механика и техн. физика. — 2001. — Т. 42. — № 4. — С. 155–160 . - Шкутин Л. И.
Численный анализ осесимметричных форм выпучивания конических оболочек // Прикл. механика и техн. физика. — 2001 — Т. 42. — № 6. — С. 159–165 .
| К началу | |