| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2005 год
Гранты российских научных фондов
- Гранты российских научных фондов
- Грант Президента РФ № МД-2130.2005.9 — «Синтез и анализ нелинейных непараметрических коллективов решающих правил в задачах распознавания образов и восстановления стохастических зависимостей»
- Грант Президента РФ № МК-982.2004.1 «Математическое и численное моделирование процессов распространения упругопластических волн в сыпучей среде»
- Грант РФФИ №
03–01–00 081 — «Разработка непараметрических систем классификации множеств случайных величин» - Грант РФФИ
03–05–20 014 БНТС-а — «Нестационарная магнитогидродинамика тонких магнитных трубок в магнитосфере» - Грант РФФИ №
04–01–00 130 «Симметрии, инварианты и дифференциальные связи уравнений с частными производными» - Грант РФФИ №
04–01–00 267 — «Разработка математических моделей и методов расчета задач механики реологически сложных сыпучих сред» - Грант РФФИ №
04–05–64 088 — «Математическое моделирование магнито-сферных МГД генераторов» - Грант РФФИ № 902.2003.1 — ведущие научные школы — «Теория и приложения задач со свободной границей»
- Грант РФФИ №
04–01–00 823 — «Кубатурные формулы, точные на системах функций» - Грант РФФИ
05–01–00 576 — «Бесконечные группы с различными условиями конечности» - Грант РФФИ №
05–01–00 579-а- «Численное моделирование динамики водных бассейнов на многопроцессорных ЭВМ» - Грант РФФИ №
05–01–00 836 — «Структуры и устойчивость течений со свободной границей в неклассических моделях конвекции» - Грант РФФИ №
05–01–10 073-г — «Организация и проведение VIII Всероссийского семинара «Моделирование неравновесных систем"" - Грант РФФИ №
05–01–10 074-г — «Организация и проведение XIII Всероссийского семинара «Нейроинформатика и ее приложения"" - Грант РФФИ №
05–01–10 087 — «Организация и проведение международной конференции «Параллельные вычислительные технологии» (PaCT-2005)» - Грант РФФИ-ККФН №
05–01–97 700_ р. Енисей — «Разработка математических моделей и компьютерных программ для исследования гидротермических режимов в озерах и водохранилищах» - Грант РФФИ №
05–03–32 642-а — «Образование и модификация наноструктур под действием оптического излучения в золях металлов: механизмы и проявления» - Грант РФФИ №
05–05–89 02 НВО — «Новая интеграционная модель функционирования озерных экосистем: стабильность и анализ управления» - Грант РФФИ-ККФН №
05–05–97 701-а «Природные ресурсы Красноярского края в показателях устойчивого развития» - Грант РФФИ №
05–07–90 201-в — «Развитие Красноярской городской информационно-вычислительной сети науки и высшей школы» - Грант РФФИ №
05–07–90 244-в — «Развитие технологий хранилищ данных и оперативной аналитической обработки (OLAP) в задачах здравоохранения» - Грант РГНФ №
03–05–12 012в «Разработка территориально распределённой информационной системы эпидемиологического мониторинга артериальной гипертонии среди населения региона» - Грант Фонда содействия отечественной науке — «Кандидаты и доктора наук РАН»
- Проект УР.03.01.101 — «Математическое моделирование распространения нестационарных неоднородностей в вязком теплопроводном газе»
Грант Президента РФ № МД-2130.2005.9 — «Синтез и анализ нелинейных непараметрических коллективов решающих правил в задачах распознавания образов и восстановления стохастических зависимостей»
Руководитель:
д.т.н., доцент В. А. Лапко
Разработаны методы синтеза и анализа структуры нелинейных непараметрических коллективов решающих правил в задачах распознавания образов в условиях неоднородных обучающих выборок большой размерности, адаптируемых к объектам различной природы. Предложены критерии оценивания показателей эффективности решающих правил при конечных объёмах обучающих выборок.
Основные публикации:
- Лапко А. В., Лапко В. А., Цугленок Г. И.
Синтез и анализ непараметрических моделей стохастических зависимостей и распознавания образов в условиях пропуска данных // Вестник КрасГАУ. — 2005. — № 7. — С. 64-70.
(Отдел вычислительной математики)
| К началу | |
Грант Президента РФ № МК-982.2004.1 «Математическое и численное моделирование процессов распространения упругопластических волн в сыпучей среде»
Руководитель:
к.ф.-м.н. О. В. Садовская
Разработанные на этапе 2004 года вычислительные алгоритмы реализованы в виде двух комплексов прикладных программ, предназначенных для исследования процессов распространения упругопластических волн в сыпучих средах в плоской и пространственной постановках. Комплексы ориентированы на использование отечественных многопроцессорных вычислительных систем серии МВС. Проведен анализ эффективности применяемых алгоритмов распараллеливания в задачах большой размерности. В пространственной постановке исследован процесс образования кумулятивного выплеска при взаимодействии ударных волн уплотнения (сигнотонов) в неоднородно разрыхленной сыпучей среде (рис. 22).
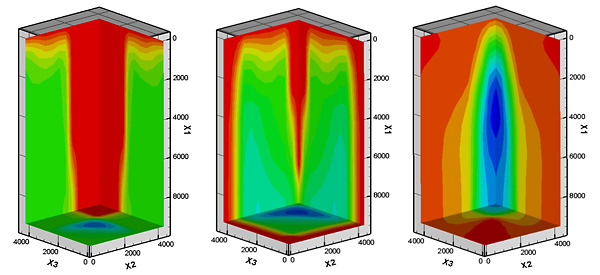
Рис. 22. Поле напряжений в задаче кумулятивного взаимодействия сигнотонов (в результате отражения искривленных волновых фронтов на центральной оси появляется кумулятивный выплеск — характерная зона сжимающих напряжений, движущаяся снизу вверх).
Основные публикации:
- Садовская О. В., Садовский В. М.
Параллельная реализация алгоритма для расчета упругопластических волн в сыпучей среде // Вычислительные методы и программирование. — 2005. — Т. 6. — С. 209–216 . - Sadovskii V. M., Sadovskaya O. V.
Parallel computation of elastic-plastic waves propagation in granular material // Proc. 7-th Int. Conf. on Mathematical and Numerical Aspects of Wave Propagation «Waves 2005». — USA, Brown University. — 2005. — P. 223–225 .
(Отдел вычислительной механики деформируемых сред)
| К началу | |
Грант РФФИ №
Руководитель:
д.т.н., проф. А. В. Лапко
Развита методика синтеза непараметрических моделей анализа множеств случайных величин на новые условия распознавания образов, учитывающих априорные сведения о виде уравнения разделяющей поверхности между классами и наличие разнотипных данных в обучающей выборке. Теоретическую основу непараметрических классификаторов составляют принципы гибридного моделирования и методы локальной аппроксимации.
Наиболее перспективными направлениями применения разработанных непараметрических моделей является обработка больших массивов статистических данных, часто встречающихся при исследовании медико-биологических и экологических систем.
Основные публикации:
- Лапко В. А., Соколов М. И., Цугленок Г. И.
Гибридные алгоритмы классификации множеств случайных величин // Вестник КрасГАУ. — 2005. — № 9. - Лапко А. В., Лапко В. А.
«Быстрый» непараметрический алгоритм классификации множеств случайных величин // Вестник КрасГАУ. — 2005. — № 10. - Лапко В. А., Соколов М. И., Цугленок Г. И.
Непараметрические модели анализа множеств случайных величин в задачах классификации // Вестник КрасГАУ. — 2004. — № 6. — С. 50-54.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ
Руководитель:
д.ф.-м.н., проф. Н. В. Еркаев
На основе линеаризованных уравнений Власова-Максвелла исследована двухпотоковая неустойчивость в двухкомпонентной плазме, состоящей из незамагниченных ионов с каппа-распределением по скоростям и замагниченных максвелловских электронов. Впервые изучено влияние параметров каппа-функции распределения ионов на инкремент модифицированной двухпотоковой неустойчивости.
Основные публикации:
- Langmayr D., Erkaev N. V., Biernat H. K.
, Influence of the ion flow direction on the modified two stream instability // Abstr. 6-th Int. Workshop on Planetary Radio Emissions. — Graz, Austria. — 2005. — P. 118.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. О. В. Капцов
Найдены инварианты характеристик уравнений газовой динамики и магнитной гидродинамики в одномерном, двумерном и трехмерном случаях. С использованием найденных инвариантов построены новые точные решения нестационарных уравнений в случае одной пространственной переменной.
Построены многочисленные примеры уравнений Эйлера-Пуассона-Дарбу, для которых найдены общие решения, зависящие от двух произвольных функций. Эти уравнения приведены к форме Мутара, что позволило использовать преобразование типа Дарбу для получения решений и рекурентных соотношений для потенциалов. Установлена связь уравнения Мутара с системой типа Тоды, уравнением нелинейной упругости и уравнением Ферми-Паста-Улама.
Основные публикации:
- Kaptsov O. V., Zabluda A. V.
Characteristic invariants and Darboux's method // J. Phys. A: Math. Gen. — 2005. — Vol. 38. — P. 3133–314 4. - Капцов О. В.
Применение преобразований Мутара-Дарбу к интегрированию дифферецальных уравнений // Препринт №3. — Красноярск: ИВМ СО РАН. — 2005. — С. 1-16. - Заблуда А. В.
Метод Дарбу и его приложения к уравнениям газовой динамики // Тез. докл. междунар. конф. «Лаврентьевские чтения по математике, механике и физике». — Новосибирск: ИГиЛ СО РАН. — 2005. — С. 46-47.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. В. М. Садовский
С помощью реологического метода, дополненного новым элементом (жестким контактом), служащим для учета различного сопротивления материала растяжению и сжатию, разработана модель развитого движения сыпучей среды. На феноменологическом уровне учитываются упругие свойства, характерные для уплотненной среды, и вязкие свойства, проявляющиеся при разрыхлении. Для описания напряженно-деформированного состояния в эйлеровых переменных применяется тензор напряжений Коши и логарифмический тензор деформаций Генки. Показано, что такой выбор тензоров обеспечивает термодинамическую корректность определяющих соотношений и приводит к адекватному описанию эффекта дилатансии при произвольной величине сдвига. В рамках разработанной ранее имитационной модели движения сыпучей среды в подвижном сосуде проведено численное моделирование процесса движения и высыпания семян через отверстия в дне вибрирующего лотка высевающего устройства. Задача рассмотрена в комплексе: высыпание из бункера в лоток и высыпание из лотка в семяводы.
На кластерах МВС-1000 ИВМ СО РАН (г. Красноярск) и МВС-15000 Межведомственного суперкомпьютерного центра (г. Москва) выполнена серия расчетов распространения поперечных волн в моментном континууме Коссера, сопровождающегося вращательным движением частиц с появлением моментных напряжений (плоская задача), и упругих волн, вызванных действием периодической импульсной нагрузки на поверхности пространственного массива (рис. 23).
Дана математическая постановка проблемы о плоских межфазных деформациях стержней и пластин из сплава с памятью формы. Задача о плоской деформации стержня и пластины в интервале фазового превращения сформулирована как нелинейная краевая задача термоупругости с неявной зависимостью от температуры. Получено аналитическое решение задачи о термоупругом сворачивании стержня в кольцо и пластины в трубу и выполнен численный анализ задачи о выпучивании стержня и пластины из сплава TiNi (никелид титана) при продольном сжатии в интервале фазового превращения.
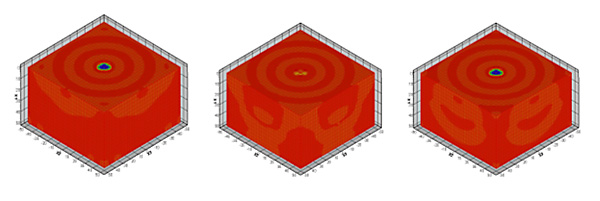
Рис. 23. Волны напряжений в упругом полупространстве (прямая задача сейсмики: результаты получены на кластере МВС-1000).
Основные публикации:
- Sadovskii V. M., Sadovskaya O. V.
Parallel computation of elastic-plastic waves propagation in granular material // Proc. 7-th Int. Conf. on Mathematical and Numerical Aspects of Wave Propagation «Waves 2005». — USA, Brown University. — 2005. — P. 223–225 . - Шкутин Л. И.
Анализ плоских межфазных деформаций стержней и пластин // Тр. IX Междунар. конф. «Современные проблемы механики сплошной среды». — Ростов-на-Дону: РГУ. — 2005. - Матвеев А. Д.
Дополнительные условия для перемещений изгибаемых композитных пластин и балок // Вестник КрасГУ. Физико-математические науки. — 2005. — № 1. — C. 211–216 .
(Отдел вычислительной механики деформируемых сред)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н. В. В. Денисенко
Рассчитаны возмущения магнитного поля в области, ограниченной магнитопаузой и поверхностью Земли, которые полагались непроницаемыми для магнитных возмущений.
В качестве источников рассмотрены магнитосферные токовые систем, образованные продольными токами, втекающими в ионосферу в авроральной области, и замыкающими их токами в ионосфере и в экваториальной плоскости магнитосферы. Для расчетов использован созданный ранее комплекс программ, позволяющий решать трехмерные задачи магнитостатики в произвольных областях (В. В. Денисенко, Н. В. Еркаев, А. В. Китаев).
Основные публикации:
- Denisenko V. V., Erkaev N. V., Semenov V. S., Biernat H. K.
Mathematical model of magnetic field perturbation by currents in the Earth's magnetosphere // Abstr. 6-th Int. Workshop on Planetary and Radio Emissions. — Graz, Austria. — 2005. — P. 117.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ № 902.2003.1 — ведущие научные школы — «Теория и приложения задач со свободной границей»
Руководитель:
чл.-корр. РАН В. В. Пухначев (ИГиЛ СО РАН)
Исполнитель от ИВМ СО РАН:
д.ф.-м.н., проф. В. К. Андреев
Для уравнений неоднородной жидкости построены точные решения, описывающие нелинейные волны (В. К. Андреев).
Предложен метод отыскания оптимальных систем подалгебр бесконечномерных алгебр Ли. Результаты применены к построению инвариантных решений уравнений термодиффузии (И. И. Рыжков).
Исследована устойчивость двух несмешивающихся слоев бинарных смесей при наличии эффекта Соре. Найдены критические числа Марангони для монотонных возмущений и построены нейтральные кривые устойчивости (М. В. Ефимова).
Основные публикации:
- Андреев В. К., Родионов А. А.
О точных решениях уравнений гидродинамической модели «глаза» тайфуна // Вычислительные технологии. — 2005. — Т. 10. — № 6. — С. 3-12. - Андреев В. К., Родионов А. А., Шанько Ю. В.
Об интегрировании осесимметрической модели «глаза» тайфуна // Дифференциальные уравнения. — 2005. — Т. 41. — № 5. — С. 1-4. - Андреев В. К.
Об уравнениях движения неоднородной жидкости // Тр. XXXVI конф. «Проблемы теорет. и прикл. математики». — Екатеринбург: ИММ УрО РАН. — 2005. — С. 107–111 . - Андреев В. К.
Об устойчивости плоского слоя со свободной границей в модели микроконвекции // Тез. докл. VI Междунар. конф. «Лаврентьевские чтения по математике, механике и физике». — Новосибирск. — 2005. — С. 103–104 . - Рыжков И. И.
Об инвариантных решениях уравнений термодиффузии // Тез. докл. VI Междунар. конф. «Лаврентьевские чтения по математике, механике и физике». — Новосибирск. — 2005. — С. 71.
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н. М. В. Носков (КГТУ)
Исполнитель от ИВМ СО РАН:
к.ф.-м.н. К. В. Симонов
Разработана эффективная вычислительная технология для анализа пространственно-временных данных сейсмомониторинга. Выполнено моделирование данных наблюдений для Караганской очаговой области сильных землетрясений.
Основные публикации:
- Носков М. В., Симонов К. В., Перетокин С. А.
Моделирование данных сейсмомониторинга // Материалы VIII Междунар. семинара «Кубатурные формулы и их приложения». — Улан-Удэ: ВСГТУ. — 2005. — С. 97-99.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ
Руководитель:
д.ф.-м.н., проф. В. П. Шунков
Изучались бесконечные группы, содержащие бесконечную систему подгрупп Фробениуса. Охарактеризованы Mp-группы. Группы с почти слойно конечной периодической частью охарактеризованы в классе локально конечных групп и получено описание силовских 2-подгрупп и некоторых двупорожденных подгрупп в группе-контрпримере. Найдены и реализованы алгоритмы поиска параметра вложения инволюций в группе. Протестированы алгоритмы построения квадрата класса сопряжённых элементов конечной группы. Построены две (из трёх) порождающих спорадическую группу B инволюций. Получены частичные ответы на вопросы 9.24, 14.69 и 14.82 из «Коуровской тетради». Указаны без округлений координаты вершин простых правильногранных тел, которые не являются ни правильными (платоновыми), ни равноугольно-полуправильными (архимедовыми), ни их частями, отсечёнными не более, чем тремя плоскостями. На базе этих координат завершено построение компьютерных моделей этих тел. Организована технологическая цепочка автоматизированного макетирования многогранников.
Основные публикации:
- Shunkov V. P.
Groups with conditions of finiteness // Acta Applicandae Mathematicae. — 2005. — № 85(1-3). — P. 277–283 . - Сенашов В. И., Созутов В. И., Шунков В. П.
Группы с условиями конечности // Успехи мат. наук. — 2005. — Т. 69. — № 5 (365). — С. 1-46.
(Отдел дискретной математики)
| К началу | |
Грант РФФИ №
Руководитель:
член-корр. РАН В. В. Шайдуров
Cоздано программное обеспечение метода конечных элементов для решения нестационарных уравнений теории мелкой воды на поверхности Земли для расчета гравитационных колебаний мирового океана и его участков.
Составлен обзор существующих математических моделей, описывающих процессы формирования стока влаги в бассейне реки. Рассмотрена система стокообразующих процессов, нуждающихся в моделировании: приток влаги в бассейн — потери стока — дорусловая трансформация стока — приток в русло — русловая трансформация стока — характеристики стока в замыкающем створе. Проведен краткий обзор подходов и методов, которые используются или могут использоваться при моделировании, описана математическая иерархия моделей. В качестве отправной точки при моделировании дорусловой и русловой трансформации стока рассмотрена модель движения вязкой несжимаемой жидкости в форме уравнений Навье-Стокса. Путем введения упрощающих гипотез последовательно описаны модели Ричардсона, мелкой воды, Сен-Венана и кинематической волны вплоть до алгебраических балансовых соотношений, широко применяемых в настоящее время на практике. Обоснована корректность математической модели паводкового изменения русла реки с учетом изменения границ, определяемых прибрежным рельефом. Проведен анализ литературы по формированию реальных параметров математической модели.
Разработан новый эффективный метод решения жестких аддитивных систем, ориентированный на решение задач механики сплошной среды после дискретизации по пространству методом конечных элементов или с помощью конечных разностей, а также на решение локально-неустойчивых задач. Построены неравенства для контроля точности и устойчивости, позволяющие проводить расчеты с переменным шагом интегрирования. Проведены численные эксперименты, подтверждающие эффективность предложенного алгоритма. В частности, при диагональной аппроксимации матрицы Якоби построенный метод на два-три порядка эффективнее современных алгоритмов на основе явных методов.
Основные публикации:
- Каменщиков Л. П., Карепова Е. Д., Шайдуров В. В.
Моделирование поверхностных волн в водоемах методом конечных элементов на вычислительном кластере // Тр. IV школы-семинара «Распределенные и кластерные вычисления». — Красноярск: ИВМ СО РАН. — 2005. — С. 114–125 . - Новиков Е. А., Каменщиков Л. П.
Параллельная реализация (2,1)-метода решения жестких систем // Тр. IV школы-семинара «Распределенные и кластерные вычисления». — Красноярск: ИВМ СО РАН. — 2005. — C. 125–135 .
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Научный руководитель:
д.ф.-м.н., проф. В. К. Андреев
Выведены уравнения малых возмущений для модели конвекции, когда плотность зависит от температуры, концентрации и давления, а на свободной границе имеются поверхностно-активные вещества. В случае плоских слоев исследована задача об устойчивости положения равновесия бинарной смеси при наличии свободной границы и поверхности раздела (В. К. Андреев, М. В. Ефимова).
На основе метода симметрии построены новые точные решения уравнений термодиффузии, описывающие стационарные течения в цилиндрических слоях (И. И. Рыжков).
Исследовано влияние эффекта Соре на движение плоского слоя с двумя свободными границами. Показано, что если среднее значение начального профиля скорости строго отрицательно, то время существования движения слоя конечно: происходит разрушение слоя (В. К. Андреев, Ю. А. Гапоненко, А. Е. Картошкина).
Для системы уравнений конвекции, полученной с помощью метода осреднений, изучено воздействие высокочастотных колебаний массовых сил на конвекцию в смешивающихся жидкостях. Исследованы структуры течений, возникающие при начальных условиях, соответствующих физическим экспериментам при пониженной гравитации (Ю. А. Гапоненко).
Исследована конвективная неустойчивость системы двух горизонтальных слоев несмешивающихся жидкостей с близкими плотностями, которые зависят нелинейным образом от давления и температуры. Показано, что состояние механического равновесия является неустойчивым. Построены нейтральные кривые и найдены критические числа Релея. При расчетах использовались значения физических параметров, характерные для различных зон Байкала: Северного, Центрального и Южного (В. К. Андреев, В. Б. Бекежанова).
Основные публикации:
- Андреев В. К., Картошкина А. Е., Родионов А. А.
Об одном уравнении динамики вязкой жидкости // Вестник КрасГУ. — 2005. — № 1. — С. 204–210 . - Андреев В. К., Бекежанова В. Б.
Конвективная неустойчивость системы горизонтальных слоев слабо сжимаемых жидкостей (направлена в ПМТФ).
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. В. В. Слабко (КГТУ)
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. А. Н. Горбань.
Конференция проводилась с 14 по 16 октября 2005 года в Институте вычислительного моделирования СО РАН. Научная программа конференции включала следующие секции: методы и технологии математического моделирования неравновесных систем, разработка математического и программного обеспечения моделирования нелинейных, нестационарных и неоднородных по пространству процессов, развитие методов имитационного моделирования сложных систем (классическое имитационное моделирование, нейронные сети, моделирование с использованием активных сред и т.п.), приложения в физике, химии, технике, биологии, медицине, экономике и финансах. На семинаре были представлены 105 докладов от 125 участников из различных регионов Российской Федерации и СНГ. Целью семинара было обсуждение и распространение современных достижений в области применения математических методов для моделирования неравновесных систем различной природы (неравновесных систем, изучаемых в различных областях науки: физике, химии, биологии, медицине, экономике и финансах). В ходе заключительной дискуссии принято решение провести следующий, 9-й семинар МНС-06 в октябре 2006 г.
Основные публикации:
Моделирование неравновесных систем — 2005 // Материалы VIII Всерос. семинара «Моделирование неравновесных систем». — Красноярск: ИВМ СО РАН. — 2005. — 245 с.
(Отдел моделирования неравновесных систем)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. А. Н. Горбань
Конференция проводилась с 7 по 9 октября 2005 года в Институте вычислительного моделирования СО РАН. Научная программа конференции включала следующие секции: архитектура и алгоритмы обучения нейронных сетей, нейросетевые экспертные системы, нейросетевое программное обеспечение и принципы его построения, нейросетевые технологии производства знаний, нейросетевые методы в медицине. На конференции были представлены 70 докладов от 126 участников из 27 городов Российской Федерации и СНГ. Принято решение о продолжении ежегодного проведения семинаров с обязательным привлечением большего числа студентов и молодежи.
Основные публикации:
Нейроинформатика и ее приложения // Материалы ХIII Всерос. семинара «Нейроинформатика и ее приложения». — Красноярск: ИВМ СО РАН. — 2005. — 153 c.
(Отдел моделирования неравновесных систем)
| К началу | |
Грант РФФИ №
Руководитель:
д.т.н., проф. В. Э. Малышкин (ИВМиМГ СО РАН)
Ответственный исполнитель от ИВМ СО РАН: член-корр. РАН В. В. Шайдуров.
Конференция проводилась с 5 по 9 сентября 2005 года в Красноярске в Доме науки и техники. Научная программа конференции включала следующие секции: математические модели, приложения формальных моделей, программирование, инструментарий, компиляция, параллельная реализация численных алгоритмов, организация вычислений, мелкозернистые вычисления. На конференцию были представлены 78 статей авторов из 20 стран. Отобрано 38 докладов авторов из 12 стран (Россия, Евросоюз, США, Южная Корея, Китай, Финляндия, Канада, Тайвань, Дания). Общее количество участников более 60.
Основные направления представленных на конференции работ: развитие средств и методов параллельной реализации алгоритмов, развитие мелкозернистых подходов к параллельной реализации математических моделей природных явлений, научные и технологические проблемы разработки сетевых средств обработки данных, программное обеспечение для кластеров и GRID-вычислений, разработка Web-ориентированных приложений для обеспечения удаленного доступа к кластерам, развитие средств конструирования параллельных программ.
Основные публикации:
Parallel Computing Technologies: 8-th International conference; proceedings / PaCT-2005. — Krasnoyarsk // Springer. — 2005. — Lecture Notes in Computer Science. — Vol. 3606. — 470 p.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ-ККФН №
Руководитель:
д.ф.-м.н., проф. В. М. Белолипецкий
Разработаны математическая модель, численные алгоритмы и компьютерные программы для исследования годового температурного режима непроточного водоема с учетом динамики ледяного покрова (в одномерном приближении). На основе разработанных численных алгоритмов и компьютерной программы выполнены расчеты стратифицированных течений (двумерных в вертикальной плоскости) для оз. Шира, установлены вертикальная и горизонтальная структуры течений.
Основные публикации:
- Белолипецкий П. В.
Численное моделирование двумерных в вертикальной плоскости ветровых течений в стратифицированных водоемах методом расщепления // Вычислительные технологии. — 2005. — Т. 10. — № 5. — С. 19-28.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н. С. В. Карпов (ИФ СО РАН)
Ответственный исполнитель от ИВМ СО РАН: к.ф.-м.н. А. П. Гаврилюк.
Создана математическая модель кинетики фотомодификации (ФМ) простейшего агрегата наночастиц (димера) в коллоидном растворе под действием лазерного излучения. В модели учтено взаимодействие между частицами: дипольное, индуцируемое лазерным излучением; электростатическое; Ван-дер-Вальсовое, а также стерическое, обусловленное существованием полимерной оболочки вокруг каждой частицы. Учитывался нагрев частицы и окружающей среды лазерным излучением, а также влияние этого нагрева на упругие свойства полимерных оболочек. В процессе фотомодификации меняется расстояние между частицами, вследствии чего меняются оптические характеристики димера, что также учтено в модели. Построенная модель позволяет описать динамику движения частиц в димере и их нагрев при лазерном воздействии, а также определить изменение его спектра в процессе ФМ и пороговые энергии ФМ при различных частотах лазерного излучения.
(Отдел вычислительной физики)
| К началу | |
Грант РФФИ №
Руководитель:
член-корреспондент РАН А. Г. Дегерменджи
Ответственный исполнитель:
д.ф.-м.н. В. М. Белолипецкий
Разработаны численные алгоритмы и компьютерные программы для исследования годового термического режима непроточного водоема с учетом ледообразования. Предложена методика для совместного исследования гидрофизических и гидробиологических процессов в непроточном водоеме (одномерное приближение).
Основные публикации:
- Белолипецкий В. М., Генова С. Н., Грицко В. В.
Компьютерная модель для исследования экологического состояния стратифицированного водоема // Тез. VIII Всерос. конф. «Современные проблемы математического моделирования природных и антропогенных катастроф». — Кемерово: ИУУ СО РАН. — 2005.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ-ККФН №
Руководитель:
д.ф.-м.н., проф. Н. Я. Шапарев
Разработана система показателей устойчивого регионального природопользования, включающая лесные, водные, земельные и минеральные ресурсы. Показатели состоят из критериев и индикаторов. Под критериями подразумеваются главные направления практической деятельности для достижения цели государственной политики при формировании основных принципов, требований и механизмов реализации гармоничного развития общества. Критерии реализуются и оцениваются по совокупности характеризующих их индикаторов, которые являются количественными и описательными характеристиками критериев устойчивого развития. Система критериев и индикаторов дает возможность оценить направление изменений в управлении ресурсами.
Основные публикации:
- Шапарев Н. Я.
Земельные ресурсы Красноярского края в показателях устойчивого развития // Сибирский экологический журнал. — 2005. — № 5. — C. 846–853 .
(Отдел вычислительной физики)
| К началу | |
Грант РФФИ №
Руководитель:
чл.-корр. РАН В. В. Шайдуров
В рамках гранта велась координация работ по соединению корпоративной сети Красноярского научного центра СО РАН с городской информационно-вычислительной сетью и предоставлению в доступ информационно-вычислительных ресурсов.
Основные публикации:
- Каменщиков Л. П.
О параллельном решении систем линейных уравнений на основе DVM-подхода с примерами приложений // Тр. V школы-семинара «Распределенные и кластерные вычисления». — Красноярск: ИВМ СО РАН. — 2005. — С. 48-50.
(Отдел вычислительной математики, лаборатория средств телекоммуникации и вычислительной техники)
| К началу | |
Грант РФФИ №
Руководитель:
д.т.н., проф. Л. Ф. Ноженкова
Выполнено проектирование и реализация математического, программного и информационного обеспечения для создания хранилищ медицинской информации и формирования информационных ресурсов системы здравоохранения и обязательного медицинского страхования. Разработаны методы и инструментальные средства OLAP-анализа, включая язык высокого уровня для построения аналитических моделей и комплексов моделей для задач здравоохранения, выполнено расширение инструментария аналитического эксперимента. Разработаны средства автоматизации обработки и загрузки данных в хранилище медицинской информации путем создания и выполнения ETL-пакетов. Методы и алгоритмы, используемые при реализации ETL-подсистемы, позволяют технологично решать основные задачи, касающиеся загрузки и очистки больших массивов медико-демографических данных в хранилище. Разработаны новые средства моделирования аналитических расчетов в OLAP-системе путем применения формульного интерфейса. Использование новых технологических средств позволило обеспечить автоматизацию обработки статистических данных и информационной поддержки задач охраны материнства и детства.
Основные публикации:
- Жучков Д. В., Никитина М. И., Струкачёв Д. В.
К вопросу о хранении и средствах обработки больших массивов данных // Материалы IX Всерос. науч.-практ. конф. «Проблемы информатизации региона». — Красноярск: ИПЦ КГТУ. — 2005. — T. 1. — С. 131–137 . - Виноградов К. А., Коробко А. В.
Построение информационно-аналитической системы «Охрана материнства и детства» на базе OLAP-компонентов // Материалы IX Всерос. науч.-практ. конф. «Проблемы информатизации региона». — Красноярск: ИПЦ КГТУ. — 2005. — T. 2. — С. 55-61. - Ишенин П. П.
Применение языковых средств в оперативной аналитической обработке данных // Материалы IX Всерос. науч.-практ. конф. «Проблемы информатизации региона». — Красноярск: ИПЦ КГТУ. — 2005. — T. 1. — С. 137–142 . - Евдокимов Д. А., Ишенин П. П., Кочетков С. Н.
Формульный интерфейс для многошаговых расчетов в системе сбора и обработки статистических данных // Материалы VI Всерос. науч.-практ. конф. «Теоретические и прикладные вопросы современных информационных технологий». — Улан-Удэ: ВСГТУ. — 2005. — С. 105–109 .
(Отдел прикладной информатики)
| К началу | |
Грант РГНФ №
Руководитель:
д.т.н., проф. А. В. Лапко
Завершена разработка информационной системы эпидемиологического мониторинга артериальной гипертонии среди населения региона и подготовлен комплект документов для администратора и операторов системы, обеспечивающих её эффективную эксплуатацию. Проведено комплексное тестирование информационной системы ЭМАГ на реальных данных Красноярского края, что позволило осуществить структурную адаптацию её подсистем. Проведена государственная регистрация информационной системы эпидемиологического мониторинга артериальной гипертонии.
Основные публикации:
- Поликарпов Л. С., Лапко А. В., Хамнагадаев И. И., Яскевич Р. А.
Метеотропные реакции сердечно-сосудистой системы и их профилактика. — Новосибирск: Наука. — 2005. — 196 с. - Лапко А. В., Лапко В. А., Якунин Ю. Ю., Константинов П. Е., Заблуда А. В., Ярославцев С. Г.
Региональная автоматизированная информационная система эпидемиологического мониторинга артериальной гипертонии // Свидетельство об отраслевой регистрации в отраслевом фонде алгоритмов и программ № 4852 (гос.регистрация № 50200500806). — 2005. - Лапко А. В., Лапко В. А., Гуревич К. Ю., Косов Р. А., Суханов А. В., Якунин Ю. Ю., Ярославцев С. Г.
Информационная система эпидемиологического мониторинга артериальной гипертонии и её развитие // Материалы IX Всерос. науч.-практ. конф. «Проблемы информатизации региона». — Красноярск: ИПЦ КГТУ. — 2005. — С. 82-84.
(Отдел вычислительной математики)
| К началу | |
Грант Фонда содействия отечественной науке — «Кандидаты и доктора наук РАН»
Руководитель:
д.т.н., доцент В. А. Лапко
Впервые с единых теоретических позиций разработаны методические и алгоритмические средства построения непараметрических систем классификации данных с пропусками, обеспечивающие рациональный учет априорных сведений и значительно повышающие вычислительную эффективность решения задач распознавания образов.
Основные публикации:
- Лапко А. В., Лапко В. А., Цугленок Г. И.
Синтез и анализ непараметрических моделей стохастических зависимостей и распознавания образов в условиях пропуска данных // Вестник КрасГАУ. — 2005. — № 7. — С. 64-70.
(Отдел вычислительной математики)
| К началу | |
Проект УР.03.01.101 — «Математическое моделирование распространения нестационарных неоднородностей в вязком теплопроводном газе»
Руководитель:
член-корр. РАН В. В. Шайдуров
Изучены особенности математической модели, описывающей сверх- гиперзвуковые течения вязкого теплопроводного газа с сильными неоднородностями. Уточнена дискретная модель, построенная ранее на основе метода конечных элементов на прямоугольных сетках. Апробирован новый тип условий на границе расчётной области. Построен эффективный вычислительный алгоритм, реализованный на многопроцессорной вычислительной системе МВС — 1000/16, на 30, 60 и 100 процессорах суперкомпьютера МВС — 1000 М с размером сеточной области 300×300, 600×600, 1200×1200.
Для периодического по времени импульса энергии большой мощности обнаружены зоны высокой плотности и повышенного давления, вырождающиеся со временем в вихревые следы за зоной взаимодействия неоднородностей (В. В. Шайдуров, Г. И. Щепановская).
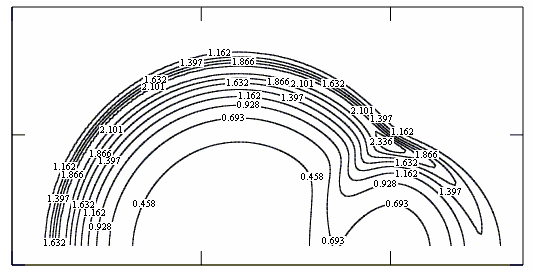
Рис. 24. Линии постоянной плотности (изохоры) при нестационарном взаимодействии двух тепловых импульсов T01, T02 в моменты времени k1, k2: T01=19, k1=1200; T02=42, k2=1600; M=4, Re=2×103.
Рассмотрена аппроксимация двумерной задачи Навье-Стокса для вязкого теплопроводного газа по пространству методом конечных элементов. Постановка задачи отличается краевыми условиями на границе расчетной области, связывающими производные скоростей и давление. Эти краевые условия являются естественными для вариационной (интегральной) постановки, т.е. не накладывают дополнительных условий на подпространства пробных и тестовых функций в отличие от главных краевых условий (типа условий Дирихле).
Для аппроксимации по пространству использован метод Бубнова-Галеркина в комбинации с методом линий. В качестве пространства пробных и тестовых функций использовано пространство функций, кусочно-билинейных на квадратных ячейках. Для вычисления интегралов по элементарным областям использована квадратурная формула метода трапеций и его двумерного аналога как декартова произведения. В итоге получена система обыкновенных дифференциальных уравнений по времени относительно четырех векторов, состоящих из значений плотности, скоростей и энергии в узлах квадратной сетки и зависящих от времени.
Для дискретного аналога доказаны некоторые свойства — дискретные аналоги непрерывных балансовых соотношений, таких как сохранение массы и полной энергии (В. В. Шайдуров, Е. Д. Карепова, Л. П. Каменщиков).
Основные публикации:
- Шайдуров В. В., Щепановская Г. И.
К вопросу о снижении плотности в набегающем потоке перед летательным аппаратом // Вестник СибГАУ. — 2005. — Вып. 6. (в печати). - Karepova E. D., Malyshev A. V., Shaidurov V. V., Shchepanovskaya G. I.
The finite element method foR the Navier-Stokes equations for a viscous heat conducting gas // Numerical Analysis and Its Applications. — Springer-Verlag Berlin Heidelberg. NAA 2004, LNCS 3401. — 2005. — P. 56-65. - Малышев А. В., Шайдуров В. В., Щепановская Г. И.
Численное решение нестационарного сверхзвукового взаимодействия тепловых импульсов // Материалы IX Междунар. конф. «Решетневские чтения». — Красноярск: СибГАУ. — 2005. — С. 260–261 . - Шайдуров В. В., Щепановская Г. И.
О краевых условиях на границе расчетной области для уравнений вязкого теплопроводного газа // VI Междунар. конф. «Лаврентьевские чтения по математике, механике и физике». — Новосибирск: ИгиЛ СО РАН. — 2005. — http://lavr05.hydro.nsc.ru/
(Отдел вычислительной математики)
| К началу | |