| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2006 год
Важнейшие научные достижения 2006 года
Перестановочная неустойчивость границы ионосферы Марса, обтекаемой солнечным ветром
Номер научного направления ОИТВС: 3
Автор научного результата:
Еркаев Н. В., в.н.с., д.ф.-м.н., проф.;
Тел.: 8
На основе численного гибридного моделирования обтекания солнечным ветром Марса при сотрудничестве с Техническим университетом г. Брауншвейга, Германия, установлено существование крупномасштабной неустойчивости границы ионосферы Марса. Показано, что в лобовой области возникают сильные возмущения обтекаемой поверхности, обусловленные развитием перестановочной неустойчивости на границе ионосферы Марса, связанной с искривленным магнитным полем в области обтекания. При этом на флангах обтекаемой границы имеет место неустойчивость Кельвина-Гельмгольца.
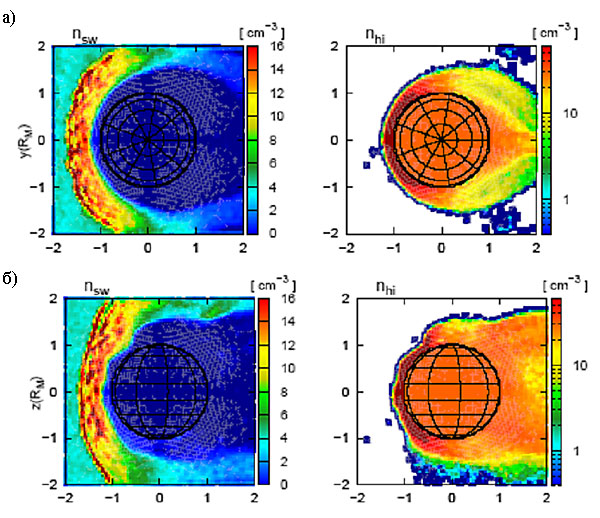
Рис. 1. Картина обтекания солнечным ветром Марса в двух плоскостях: а) в плоскости эклиптики XY, параллельной межпланетному полю; б) в плоскости XZ, ортогональной межпланетному магнитному полю.
На рис. 1 показаны распределения плотности частиц солнечного ветра (nsw), а также плотности ионосферных ионов (nhi), полученные в результате численного моделирования. Верхние рисунки (а) соответствуют плоскости межпланетного магнитного поля, а нижние рисунки (б) — ортогональной магнитному полю плоскости. На рисунках видна довольно четкая граница, отделяющая протоны солнечного ветра от ионосферных ионов, которая выглядит совершенно невозмущенной в плоскости XY. Совершенно другая картина наблюдается в плоскости XZ, где видны сильные волновые деформации границы обтекания. Это означает, что волновой вектор неустойчивых возмущений ортогонален магнитному полю, что хорошо согласуется с теорией перестановочной неустойчивости. Кроме того, теоретическая оценка обратного инкремента перестановочной неустойчивости вполне соответствует характерному времени нарастания возмущений в численном эксперименте.
Важнейшие публикации:
- Arshukova I. L., Erkaev N. V., Biernat H. K.
Magnetohydrodynamic instability of a high magnetic shear layer with a finite curvature radius // Physics of plasmas. — 2002. — Vol. 9. — № 2. — P. 401–408 . - Arshukova I. L., Erkaev N. V., Biernat H. K., Vogl D. F.
Interchange instability of the Venusian ionopause // Advances in Space Research. — 2004. — Vol. 33. — 182186. - Arshukova I. L., Erkaev N. V., Biernat H. K.
Interchange instability of a curved current layer with smooth monotonic variations of the magnetic field components // Ann. Geophys. — 2004. — Vol. 22. — 993999.
| К началу | |
Топологические грамматики и аппроксимация многомерных данных
Номер научного направления ОИТВС: 3
Авторы научного результата:
Горбань А. Н., зав. отд., д.ф.-м.н., проф.;
Зиновьев А. Ю., н.с., к.ф.-м.н.;
Тел.: 8
Разработан метод топологических грамматик для аппроксимации многомерных данных. Для данных сложной топологии определены главные кубические комплексы — нелинейный и ветвящийся аналог главных компонент. Проблема построения оптимального главного комплекса представлена как серия задач минимизации квадратичных функционалов с разреженной матрицей. Главный комплекс представлен как произведение одномерных континуумов — нелинейных ветвящихся главных компонент. Элементарные преобразования грамматик применяются к факторам. Эффективность процесса определяется факторизацией на одномерные преобразования и минимизацией квадратичных функционалов с разреженной матрицей. Уже первые главные компоненты позволяют эффективно визуализировать и анализировать сложные структуры данных (рис. 2).
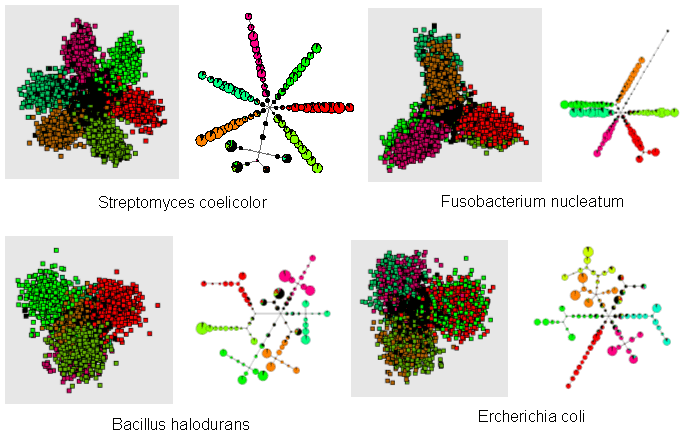
Рис. 2. Визуализация триплетного состава геномов с помощью линейных и ветвящихся нелинейных главных компонент. Слева — вид в пространстве первых трех главных компонент (каждая точка изображает триплетный состав в скользящем окне шириной 4
Важнейшие публикации:
- Gorban A. N., Sumner N. R., Zinovyev A. Y.
Topological grammars for data approximation // Applied Mathematics Letters. — 2006. — doi:10.1016/ j.aml.2006. 04.022.
| К началу | |