| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2006 год
Программы фундаментальных исследований Сибирского отделения РАН
- Программы фундаментальных исследований Сибирского отделения РАН
- Проект № 2.2.7 «Разработка математических моделей гидрофизики, теплофизики и биофизики, вычислительных алгоритмов и программ для исследования микросистем термостабилизации космических аппаратов и режимов речных и озерных экосистем»
- Проект № 3.1.2 «Разработка гибридных интеллектуальных информационных технологий на основе интеграции геоинформационных, нейросетевых, экспертных и аналитических систем»
- Проект № 4.1.3 «Математическое и компьютерное моделирование задач механики с поверхностями раздела»
- Проект № 8.3.6 «Теория и методы моделирования разрушений, аварийных ситуаций и риск-анализа конструкций технических систем»
- Проект № 8.3.7 «Структурная теория пластичности и разрушения гетерогенных, волокнистых композитных материалов и конструкций»
Направление 2:
Прикладная математика
Программа 2.2:
Математическое моделирование
№ гос. регистрации 0120.0 409304
Научный руководитель проекта:
чл.-корр. РАН В. В. Шайдуров
Блок 2. Построение математической модели переноса геомагнитного поля в хвосте магнитосферы и сопутствующей генерации электрического поля. Численное исследование процесса нарастания магнитного потока в долях хвоста.
Построена математическая модель переноса геомагнитного поля в хвосте магнитосферы и сопутствующей генерации электрического поля. Плазменный слой полагается проводником, движущимся с заданным распределением скорости. Для магнитного поля считается заданным геомагнитный диполь, запертый внутри магнитопаузы заданной формы. Возмущение магнитного поля и нарастания магнитного потока в созданной модели обусловлено токами в плазменном слое, сопровождающими диффузию магнитного поля в проводнике, который движется в неоднородном магнитном поле. При этом также генерируются электрические поля (В. В. Денисенко).
Блок 3. Численное моделирование одно- и многократного рассеяния света в биологических взвесях.
Разработаны методика и алгоритм расчета индикатрис рассеяния суспензиями эритроцитов в приближении лучевой оптики. Математически задача расчета характеристик светорассеяния весьма трудоемка и часто решается моделированием методами Монте-Карло. Стоит отметить еще один аспект — задача нахождения индикатрисы светорассеяния произвольной одиночной частицей в настоящее время, строго говоря, не имеет решения. В этом случае наиболее часто в качестве индикатрис используют угловые зависимости рассеяния для сферических частиц, а также фазовые функции Хени-Гринштайна.
На рис. 3 приведены результаты Монте-Карло-моделирования светорассеяния 100 мкм слоя крови с использованием моделей хаотично ориентированных частиц сфероидальных форм, полученных с помощью гибридной аппроксимации и лучевой оптики. Результаты сравниваются с численными расчетами с использованием функции Хени-Гринштайна (g = 0.972, где g — параметр анизотропии рассеяния), а также с литературными данными. Отмечается хорошее совпадение экспериментальной кривой и результатов Монте-Карло-моделирования с индикатрисой, рассчитанной в приближении лучевой оптики.
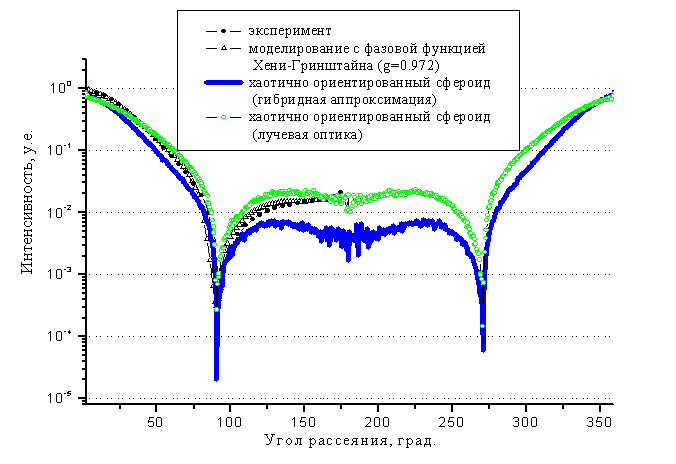
Рис. 3. Угловые зависимости интенсивностей многократно рассеянного света толстым 100-микронным слоем крови для длины волны 514 нм
При применении предложенных аппроксимаций индикатрис однократного рассеяния метод Монте-Карло позволяет получать не только индикатрису многократного рассеяния слоя крови, но и решать обратную задачу о форме частиц суспензии, тогда как моделирование рассеяния слоя крови фазовой функцией Хени-Гринштайна дает только параметр анизотропии g, причем далекий от параметра анизотропии реального эритроцита (В. Н. Лопатин).
Блок 4. Исследование количественных закономерностей функциональной организации водных экосистем.
Предложена методика и алгоритм расчета доли растворенного органического вещества (РОВ), поглощение света которой в ближней ультрафиолетовой и видимой областях спектра пропорционально содержанию РОВ в природных водах. Методика апробирована в полевых исследованиях на р. Енисее, р. Ангаре, Красноярском водохранилище. В исследованных водных объектах между интенсивностью свечения (Iф) и поглощения света РОВ (для λ > 390 нм), с одной стороны, и концентрацией РОВ — с другой, наблюдается слабая связь, которая определяется тем обстоятельством, что в этих областях спектра вклад отдельных компонентов РОВ в поглощение света не пропорционален их содержанию в воде (рис. 4).
Часть РОВ, которая ответственна за поглощение на длинах волн больше λ0 = 200 нм, можно определить следующим соотношением: Ср / С = К2exp[-(μ-μg)(λ-λ0)], где μg — коэффициент μ = dln(κ) / dλ для раствора гуминовых кислот, Ср — содержание части РОВ, которая поглощает свет на длине волны λ, К2 — коэффициент, определяющий долю хромофоров гуминовых кислот (А. Д. Апонасенко).
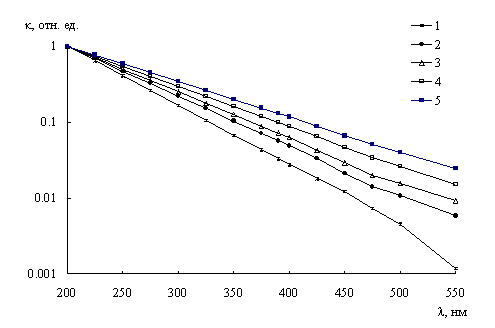
Рис. 4. Нормированные спектральные характеристики поглощения света. 1-4 — р. Ангара (635, 215, 30, 41 км соответственно), 5 — раствор гуминовых кислот
Блок 5. Разработка модели связей потоков СО2 на границе вода-атмосфера с биотой водоема.
Предложена модель связи содержания углекислого газа в поверхностном слое воды с содержанием фитопланктона, разработанная на основе серии экспериментов, которые показали, что газообмен СО2 в системе поверхность воды Байкала — атмосфера имеет ярко выраженный суточный ход, амплитуда которого превалирует над всеми другими атмосферными факторами. Очень четкая связь этого хода с продолжительностью инсоляции указывает на ведущую роль биоты Байкала в регулировании газообмена. Зависимость концентрации СО2 в поверхностном слое воды от максимального уровня флуоресценции F фитопланктона с коэффициентом корреляции r = 0.98 выражается уравнением: СО2 = 1.53 − 0.36F. Содержание СО2 в поверхностной воде зависит не только от деятельности водных гидробионтов, но и от ряда иных процессов, таких как растворимость, газообмен с атмосферой, диффузия и т.п. Вариации в водной биоте в конкретной измерительной точке также определяются не только процессом фотосинтеза, но регулируются своими жизненными циклами и своей пространственно-временной изменчивостью. Эксперимент показывает, что именно биологическая составляющая, в основном, и лимитирует содержание углекислого газа в поверхностной воде (В. В. Заворуев).
Блок 6. Разработка упрощенных вычислительных моделей для исследования динамики плотностной стратификации озер и водохранилищ за годовой период.
Разработана одномерная в вертикальном направлении математическая модель температурного и солевого режимов озера с учетом ледообразования. Предложена упрощенная модель для оценки динамики толщины ледяного покрова с учетом слоя конвективного перемешивания воды. Моделируются процессы таяния льда в весенний период как с нижней поверхности ледяного покрова, так и с верхней. Выполнены модельные расчеты. Разработанная одномерная модель позволяет исследовать динамику вертикальных распределений температуры и солености водоема с учетом образования и таяния льда. На рис. 5 приведена схема структуры водоема в вертикальном направлении.
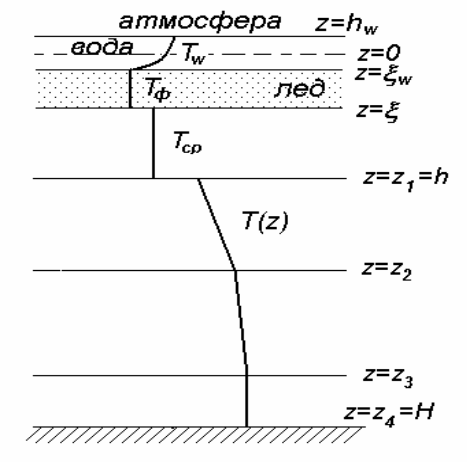
Рис. 5. Схема вертикальной структуры озера в зимний период: T — температура, z — вертикальная координата, z = H — дно, z = ξw — положение верхней поверхности ледяного покрова, z = ξ — положение нижней поверхности ледяного покрова, z = hw — граница поверхности воды
Блок 7. Создание программного комплекса решения трехмерных уравнений Навье-Стокса динамики вязкой теплопроводной сжимаемой среды с фазовыми переходами.
Уравнения Навье-Стокса для вязкой сжимаемой теплопроводной среды в полной постановке приведены к виду, допускающему исследование и обоснование устойчивости в гильбертовых пространствах в отличие от традиционной формулировки законов сохранения. Это позволило провести дискретизацию задачи по пространству методом конечных элементов с выполнением законов сохранения на дискретном уровне. Дискретизация по времени обеспечила минимальную вычислительную вязкость, пренебрежимую в сравнении с физической вязкостью при расчетах на современных высокопроизводительных ЭВМ. Начаты систематические вычислительные эксперименты для сферически-симметричных течений. Использование соответствующих уравнений состояния и обезразмеривание данных позволяет решать задачи как в области газовой динамики, так и в области глобальной геофизики. Для геофизических задач разработан эффективный метод учета гравитационных сил, обеспечивающий экономичное вычисление системы пространственных интегралов с помощью специальной модификации дискретного преобразования Фурье.
Блок 8. Разработка и реализация высокопараллельных кинетических методов моделирования сплошной среды в широком диапазоне чисел Прандтля для химически реагирующих плотных газов.
Проведен систематический анализ методов огрубления описания в статистической физике, динамике и механике сплошной среды. Построена кинетическая теория фильтрации уравнений, которая позволила в явном виде найти границу устойчивости фильтрованных уравнений. Теория апробирована на многомасштабных задачах вычислительной гидродинамики. Построена система устойчивых методов второго порядка точности для кинетического моделирования механики сплошных сред. Методы апробированы на стандартных тестовых задачах вычислительной гидродинамики и позволяют строить решение, свободное от паразитных осцилляций, локальных накоплений ошибок и удовлетворяющее первому и второму началам термодинамики.
Основные публикации:
- Denisenko V. V., Biernat H. K., Erkaev N. V., Semenov V. S.
Mathematical model of magnetic field perturbations by currents in the Earth's magnetosphere // Proc. 6-th Int. Conf. «Planetary Radio Emissions VI». — Austrian Academy of Sciences Press, Vienna. — 2006. — P. 309–316 . - Aponasenko A. D.
Optical and fluorescent characteristics of dissolved organic matter // Abstr. XIII Int. Symp. «Atmospheric and Ocean Optics. Atmospheric Physics». — Tomsk: IAO SB RAS. — 2006. — P. 161. - Панченко М. В., Заворуев В. В., Домышева В. М., Сакирко М. В., Белых О. И., Поповская Г. И.
О связи интенсивности фотосинтеза в поверхностной воде оз. Байкал с процессом газообмена СО2 // Материалы междунар. конф. «Проблемы устойчивого функционирования водных и наземых экосистем». — Ростов-на-Дону. — 2006. — С. 316–318 . - Белолипецкий В. М., Генова С. Н.
Одномерная модель вертикальной структуры озера. Температурный и солевой режимы озера // Тр. междунар. конф. «Вычислительные и информационные технологии в науке, технике и образовании». — Павлодар: ТОО НПФ «ЭКО». — 2006. — T. 1. — С. 253–261 . - Brownlee R. A., Gorban A. N., Levesley J.
Stabilization of the lattice Boltzmann method using the Ehrenfests' coarse-graining idea // Phys. Review E. — 2006. — Vol. 74. — 037703 (4 Р). - Ansumali S., Karlin I. V., Frouzakis C. E., Boulouchos K.
Entropic lattice Boltzmann method for microflows // Phys. A. — 2006. — Vol. 359. — P. 289–305 . - Karlin I. V., Ansumali S., Frouzakis C. E., Chikatamarla S. S.
Elements of the lattice Boltzmann method I. Linear advection equation // Commun. Comput. Phys. — 2006. — 1(4). — P. 616–665 . - Gorban A. N., Karlin I. V.
Quasi-equilibrium closure hierarchies for the Boltzmann equation // Phys. A. — 2006. — Vol. 360. — P. 325–364 . - Tosi F., Ubertini S., Succi S., Chen H., Karlin I. V.
A comparison of single-time relaxation lattice Boltzmann schemes with enhanced stability // Int. J. Mod. Phys. — 2006. — Vol. 17. — P. 1375–139 0.
(Отделы вычислительной математики, моделирования неравновесных систем, вычислительных моделей в гидрофизике, вычислительной физики)
| К началу | |
Направление 3:
Фундаментальные и технологические проблемы информационных, телекоммуникационных и вычислительных систем
Программа 3.1:
Информационное и математическое моделирование в различных областях знаний, задачи поддержки принятия решений, экспертные системы, теоретическое и системное программирование
№ гос. регистрации 0120.0 409302
Научный руководитель проекта:
д.т.н., проф. Л. Ф. Ноженкова
Блок 1. Гибридные методы аппроксимация многомерных данных.
Разработан метод топологических грамматик для аппроксимации многомерных данных. Для данных сложной топологии определены главные кубические комплексы — нелинейный и ветвящийся аналог главных компонент. Проблема построения оптимального главного комплекса представлена как серия задач минимизации квадратичных функционалов разреженной матрицей. Главный комплекс представлен как произведение одномерных континуумов — нелинейных ветвящихся главных компонент. Элементарные преобразования грамматик применяются к факторам. Эффективность процесса определяется факторизацией на одномерные преобразования и минимизацией квадратичных функционалов с разреженной матрицей. Уже первые главные компоненты позволяют эффективно визуализировать и анализировать сложные структуры данных. На языке Java разработан программный пакет для построения ветвящихся главных компонент и опробован на различных задачах (анализ симулированных данных, данные по цветам ириса, аппроксимация молекулярной поверхности, анализ семи-кластерной структуры генома) (А. Н. Горбань, А. Ю. Зиновьев).
Метод ветвящихся главных компонент, построенный на основе теории топологических грамматик для аппроксимации данных был применен для анализа семи-кластерной структуры генома различных организмов. Было показано, что единственная ветвящаяся главная компонента может обнаруживать наличие кластерной структуры, которая не обнаруживается с помощью трех первых линейных главных компонент. В сотрудничестве с Институтом Кюри (Париж, Франция) и лабораторией Кавендиша (Кембридж, Англия) более чем для 800 организмов был проведен анализ соотношения кодирующей и некодирующей части генома. Был показан кардинально различный характер соотношения этих частей генома для прокариотов и эукариотов. На основе модели «ускоренных генных сетей» (accelerated gene networks) выдвинута гипотеза о существенном вкладе некодирующей части генома в регуляцию генов для эукариотов. Для различных геномов были получены оценки минимально необходимой длины некодирующей части для обеспечения регуляции процессов в клетке.
В сотрудничестве с Институтом Кюри проводился анализ данных экспрессии генов при различных формах рака. Для визуализации данных экспрессии генов на основе метода упругих карт А. Ю. Зиновьевым разработано Java-приложение VIMIDA (VIsualization of MIcroarray DAta), доступное с сайта: http://bioinfo.curie.fr/projects/vimida/.
В сотрудничестве с Институтом Кюри и Центром Вычислительной Биологии в Парижской Школе Геологии (Ecole des Mines de Paris) разработан метод анализа данных экспрессии генов. Метод основан на спектральном анализе оператора Лапласа, определенного на графе, ассоциированом с генной сетью, и позволяет регуляризовать методы классификации данных экспрессии генов. Метод был применен для классификации и интерпретации результатов экспериментов по радиоактивному облучению культуры дрожжей с целью исследования влияния малых доз облучения на рост дрожжевых клеток.
Разработан метод восстановления пропущенных данных в символьных последовательностях. Для эффективного заполнения данных предложен модифицированный имитатор кинетической машины Кирдина, специализированный для данной задачи. При выборе наиболее подходящего заполнения используется метод максимального подобия полученного заполнения известной части последовательности. Получены оценки количества заполнений пропусков в символьной последовательности с использованием матричного представления частотного словаря (М. Г. Садовский, М. Ю. Сенашова, А. Г. Рубцов).
Разработан и исследован метод восстановления выхода динамического объекта непараметрической регрессионной моделью. Основной вывод состоит в том, что объекты высокого (неизвестного) порядка можно восстанавливать с приемлемым качеством моделью, соответствующей первому порядку дифференциального уравнения. Разработан и исследован метод восстановления разделяющей поверхности в явном виде в задаче распознавания образов. Разработан итерационный алгоритм идентификации выбросов в задаче восстановления регрессии (Е. С. Кирик).
Блок 2. Технологии оперативной аналитической обработки данных.
Разработано алгоритмическое и программное обеспечение для реализации новых функциональных элементов OnLine Analytical Processing (OLAP)-технологии, расширяющих возможности оперативной аналитической обработки данных за счет выполнения комплексных аналитических расчетов и средств построения специализированных OLAP-ориентированных приложений. Разработана оригинальная OLAP-машина, включающая средства построения витрин данных, средства выполнения произвольных аналитических запросов, средства представления и обработки многомерных данных, обладающие уникальными функциями: в качестве измерений могут использоваться составные иерархии со сложными оглавлениями. OLAP-машина может встраиваться в разные приложения и работать с базами данных разных форматов. Разработаны языковые, алгоритмические и программные средства, обеспечивающие реализацию сложных многошаговых аналитических расчетов путем создания комплексов OLAP-моделей, наследующих данные. Для реализации поставленной задачи предложен и реализован оригинальный подход к анализу информации, позволяющий использовать в рамках одного расчета несколько многомерных информационных кубов. Впервые разработаны программные средства для автоматизации создания OLAP-приложений: инструментальное ядро в виде набора компонент, связанных с OLAP-машиной, среда проектирования экранных форм пользовательского интерфейса, мастер быстрого создания приложений. Исследованы проблемы построения хранилищ данных для информационно-аналитических систем (Л. Ф. Ноженкова, П. П. Ишенин, А. В. Коробко, С. В. Кочетков, О. С. Исаева, Д. В. Жучков).
Выполнена интеграция средств геоинформационного моделирования и технологии оперативной аналитической обработки данных OLAP. Созданы методы динамической связи картографических объектов с многомерными данными OLAP-системы. Тематическое картографирование в OLAP-системе позволило повысить наглядность представления результатов OLAP-анализа, данные, имеющие картографическую привязку, представляются в виде картографических объектов. В основе механизма динамической связи карты и источников данных OLAP-системы лежит картографическая привязка данных через измерения, связанные со слоями электронной карты. Для повышения оперативности работы с изменяющимися пространственно-распределенными данными разработаны принципы динамического формирования картографических слоев. В OLAP-систему добавлен инструментарий, осуществляющий возможность динамического формирования слоев и геомоделирования результатов OLAP-анализа. Динамические слои позволяют представлять на карте объекты, существование, местоположение и форма которых может изменяться в зависимости от данных, поступивших из OLAP-системы (Л. Ф. Ноженкова, А. А. Евсюков, П. П. Ишенин).
Продолжено исследование возможностей применения аппарата нечеткой логики в системах поддержки принятия решений. В качестве областей приложения нечеткого подхода рассматривались задачи комплексного анализа показателей здравоохранения и задачи прогнозирования и предупреждения чрезвычайных ситуаций на основе экспертных оценок. Объединение функционального блока агрегирования данных на основе нечеткого вывода с геоинформационной системой выводит анализ данных на качественно новый уровень. Преимущества заключаются в возможности использовать единое информационное пространство исходных данных для нечеткого вывода и результаты вывода — для визуализации в виде картограмм, диаграмм и таблиц данных (О. С. Исаева, С. В. Исаев).
Блок 3. Технологии и системы создания распределенных информационных ресурсов и обеспечения безопасности в научно-образовательных сетях.
Выполнено проектирование и создание распределённых информационных ресурсов и сводных каталогов библиотек. Для создания распределённых ресурсов использовалась технология объединения баз данных, заложенная в сетевые протоколы Z39.50. Использовались возможности сервера ZooPARK, позволяющего объединить различные базы данных в логические группы и выполнять операции с этими логическими группами как с физическими базами данных. Эта технология позволяет выполнять параллельный поиск в базах данных, организуя отдельный поток для каждой базы, включить все информационные ресурсы города Красноярска в единое информационное пространство и объединить каталоги четырёх крупнейших вузов Красноярска (КГТУ, СибГТУ, СибГАУ, КрасГУ), ГУНБ Красноярского края, пяти библиотек КНЦ СО РАН, СибНИИ охотничьего хозяйства, а также каталоги московской, новосибирской, томской и омской корпоративных библиотечных систем. Ведутся работы по обеспечению доступа к зарубежным и отечественным полнотекстовым ресурсам. Выполнено исследование проблем комплексной информационной безопасности в научно-образовательных компьютерных сетях (Е. В. Ковязина, С. В. Исаев, А. В. Малышев, Д. Д. Кононов).
Для задач информационной безопасности корпоративных сетей предложены математические модели, позволяющие прогнозировать развитие угроз для конфиденциальности, целостности, доступности информации на этапе проектирования корпоративных сетей (А. Н. Рогалев).
Блок 4. Гибридные интеллектуальные технологии поддержки принятия решений.
Предложена и апробирована оригинальная реализация продукционно-фреймовой модели представления знаний в экспертной геоинформационной системе, позволяющая управлять компонентами программной среды, выбирать стратегию решения задачи на основе диалога с пользователем. Модель представляет собой модифицируемую оболочку-конструктор интеллектуальных систем поддержки управления в чрезвычайных ситуациях (ЧС). Модель позволяет не только формировать прогноз сценария ЧС на основе численного и картографического моделирования, но и строить рекомендации для формирования управленческих решений, в том числе путем подбора аналогий из базы прецедентов (С. В. Исаев, В. В. Ничепорчук, А. А. Марков, А. А. Евсюков, Р. А. Морозов).
Блок 5. Методические и программные средства исследования глобальной биоты и динамики климата.
С использованием спутниковых данных продолжены исследования взаимодействия глобальной биоты и динамики климата. Выполнена типизация аномалий концентрации хлорофилла в Мировом океане, разработана методика выявления зон нестабильности сезонной динамики океана по концентрации хлорофилла (по данным SeaWiFS). Продолжена разработка программного комплекса для исследования территориальных особенностей климата, позволяющего создавать тематические карты и диаграммы, демонстрирующие сходство и различие в тенденциях изменения климатических параметров для территории Сибири. Продолжено исследование экстремальных явлений, связанных как с температурой, так и с осадками. Используется список индексов для определения экстремальных явлений совместной рабочей группой World Meteorological Organization — Commission for Climatology и Research Program on Climate Variability and Predictability. Этот список состоит из более чем 50 индексов и доступен на http://www.knmi.nl/samenw/eca. Продолжено исследование влияния ГЭС на климат различных городов Сибири. Для Иркутска выявлено, что характер климатических изменений до постройки Иркутской ГЭС совпадал с климатическими изменениями Улан-Удэ. В настоящее время характер климатических изменений для Иркутска отличается как от Улан-Удэ, так и от других городов Сибири, что несомненно указывает на локальный характер происходящих там климатических процессов (Г. С. Высоцкая).
Блок 6. Методология нелинейных непараметрических коллективов решающих правил в задачах распознавания образов.
Разработаны теоретические основы синтеза и анализа структуры нелинейных непараметрических коллективов решающих правил в задачах распознавания образов, основанных на принципах декомпозиции систем и последовательных процедурах формирования решений, обеспечивающих эффективное использование информации неоднородных обучающих выборок большой размерности. Идея предлагаемого подхода состоит в построении семейства локальных решающих функций на основании однородных частей обучающей выборки и последующей их организации в нелинейном решающем правиле с помощью методов непараметрической статистики. Однородная часть обучающей выборки содержит её элементы, удовлетворяющие одному или нескольким требованиям, таким как наличие однотипных признаков (непрерывные, дискретные, лингвистические и др.), отсутствие либо наличие пропусков данных и др. При наличии априорных сведений о виде уравнения разделяющей поверхности в пространстве признаков ограниченной размерности они используются в виде частных решающих функций в нелинейном непараметрическом коллективе (А. В. Лапко, В. А. Лапко).
Блок 7. Геоинформационные веб-технологии.
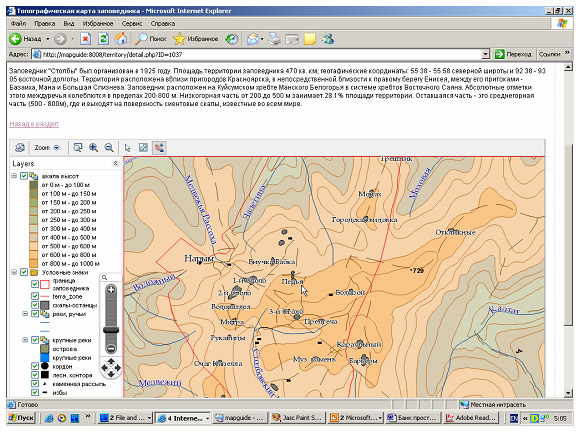
Рис. 6. Веб-интерфейс к цифровой модели территории заповедника «Столбы» на геоинформационном Интернет-портале ИВМ СО РАН
Разработаны методические, алгоритмические и программные средства для формирования геоинформационного Интернет-портала и его картоориентированных информационно-аналитических сервисов, банка геопространственных данных. В основе разработки лежит комплекс интегрированных информационных и телекоммуникационных технологий, адаптированных к применению в составе распределенных информационно-аналитических Интернет-систем, предназначенных для решения задач, связанных с динамическим формированием наборов пространственных данных, построением тематических интерактивных карт и картограмм на основе топологических связи пространственной и семантической информации, обработкой данных спутникового экологического мониторинга. Специализированная ГИС-библиотека включает в себя клиентское программное обеспечение (набор скриптовых программ на языке JavaScript и шаблонов элементов пользовательского интерфейса) и серверное программное обеспечение с применением PHP. В составе геоинформационного Интернет-портала разработано многоуровневое хранилище спутниковых снимков высокого разрешения, наполненное для территории Красноярского края, с развитыми средствами доступа, расширенными интерфейсами для просмотра данных и их программной обработки. Апробация предложенных методов и технологий была проведена на ряде конкретных задач — создании комплексных цифровых моделей природных территорий (заповедники «Столбы» и «Центральносибирский»), мониторинге качества водных ресурсов на примере анализа водно-солевого режима речной сети (в заповеднике «Центральносибирский») и др. (О. Э. Якубайлик, А. А. Кадочников, А. А. Токарев, В. Г. Попов).
Основные публикации (по блокам).
К блоку 1:
- Gorban A. N., Sumner N. R., Zinovyev A. Y.
Topological grammars for data approximation // Applied Mathematics Letters, 2006, doi:10.1016/ j.aml. — 2006. 04.022. - Radulescu O., Gorban A., Vakulenko S., Zinovyev A.
Hierarchies and modules in complex biological systems // Proc. European Conf. on Complex Systems 2006. — Oxford, UK. — 2006. — P. 152–156 . - Кирик Е. С., Шроер В., Ян Х. Ю.
Численный метод идентификации падения напряжения в стеке топливных элементов // Автометрия. — 2006. — Вып. 2. — С. 80-89. - Сенашова М. Ю., Садовский М. Г., Рубцов А. Г.
Кинетическая машина Кирдина в проблеме восстановления отсутствующих фрагментов символьных последовательностей // Ползуновский альманах. — Барнаул. — 2006. — № 11. — С. 131–133 . - Сенашова М. Ю., Рубцов А. Г., Садовский М. Г.
Применение кинетической машины Кирдина для восстановления утерянных данных в символьных последовательностях // Тр. XI Междунар. конф. «Информационные и математические технологии в научных исследованиях». — Иркутск: ИСЭМ СО РАН. — 2006. — Ч. II. — С. 168–176 . - Рубцов А. Г., Сенашова М. Ю., Садовский М. Г.
Принцип максимального подобия в проблеме восстановления утерянных данных // Материалы XIV Всерос. семинара «Нейроинформатика и ее приложения». — Красноярск: ИВМ СО РАН. — 2006. — C. 88-90.
К блоку 2:
- Евсюков А. А., Ноженкова Л. Ф.
Оперативное геомоделирование сети медицинских учреждений // Вестник КрасГАУ. — 2006. — № 13. — С. 114–118 . - Исаева О. С. Шалдыбина К. В.
Проблемы построения специализированного хранилища демографических данных // Вестник КрасГУ. «Физико-математические науки». — Красноярск: КрасГУ. — 2006. — № 1. — С. 222–227 . - Ноженков А. И., Коробко А. В., Никитина М. И.
Информационно-аналитическая поддержка формирования территориальной программы бесплатной медицинской помощи // Вестник КрасГАУ. — 2006. — № 13. — С. 108–113 . - Жучков Д. В.
Автоматизация обработки больших массивов данных // Открытое образование (Приложение). — Красноярск: ООО «Экспресс-Офсет». — 2006. — С. 56-62. - Кочетков С. Н.
Использование формального представления OLAP-модели для реализации формульного интерфейса в аналитической системе // Открытое образование (Приложение). — Красноярск: ООО «Экспресс-Офсет». — 2006. — С.98–101 . - Исаев С. В., Исаева О. С., Ноженкова Л. Ф.
Использование нечеткой логики в системах поддержки принятия решений // Материалы II Всерос. конф. «Инфокоммуникационные и вычислительные системы и технологии (ИКВТС-06)». — Улан-Удэ: Бурятский ун-т. — 2006. — Т. 1. — С. 162–168 .
К блоку 3:
- Ковязина Е. В.
Принципиальная основа, функциональные особенности и информационное наполнение библиотечно-информационной сети КНЦ СО РАН // Материалы всерос. конф. «Повышение качества непрерывного профессионального образования». — Красноярск: КГТУ. — 2006. — Ч. 2. — С. 339–343 . - Исаев С. В., Малышев А. В.
Проблемы обеспечения комплексной информационной безопасности в научно-образовательных компьютерных сетях // Вестник КрасГУ. «Физико-математические науки». — 2006. — № 1. — С. 222–226 . - Кононов Д. Д., Исаев С. В.
Обеспечение безопасности веб-приложений на примере веб-сервера ИВМ СО РАН // Вестник ТГУ (Приложение). — 2006. — № 17. — С. 156–161 . - Рогалев А. Н.
Некоторые задачи оценки параметров хаотических движений // Тр. междунар. конф. «Вычислительные и информационные технологии в науке, технике и образовании». — Павлодар: ТОО НПФ «Эко». — 2006. — T. 2. — C. 159–165 .
К блоку 4:
- Марков А. А.
Разработка многопользовательского интерфейса системы по техногенным авариям // Открытое образование (Приложение). — Красноярск: ООО «Экспресс-Офсет». — 2006. — С. 125–129 . - Исаев С. В., Морозов Р. В., Ничепорчук В. В.
Методы построения систем поддержки принятия решений в чрезвычайных ситуациях // Тр. VII Междунар. симп. «Интеллектуальные системы». — М.: РУСАКИ. — 2006. — С. 321–325 . - Ничепорчук В. В.
Разработка экспертной геоинформационной системы по техногенным авариям // Материалы науч.-практ. конф. «Проблемы снижения риска и смягчения последствий чрезвычайных ситуаций природного и техногенного характера на территории Сибирского региона». — Новосибирск. — 2006. — С. 77-79.
К блоку 5:
- Шевырногов А. П., Сидько А. Ф., Чернецкий М. Ю., Высоцкая Г. С.
Оценка зон цветения фитопланктона на Красноярском водохранилище на основе спутниковых данных AVHRR и MODIS // Исследование Земли из космоса. — 2006. — № 2. — С. 89-96. - Шевырногов А. П., Сидько А. Ф., Чернецкий М. Ю., Высоцкая Г. С.
Анализ динамики отражательной способности хвойных и лиственных древостоев на территории Красноярского края по наземным и спутниковым измерениям // Исследование Земли из космоса. — 2006. — № 2. — С. 71-78.
К блоку 6:
- Лапко А. В., Лапко В. А., Ярославцев С. Г.
Разработка и исследование гибридных алгоритмов в задачах распознавания образов // Автометрия. — 2006. — № 1. — С. 32-39. - Лапко В. А., Бадмаев Р. В., Капустин А. Н.
Нелинейные непараметрические коллективы решающих правил // Вестник КрасГАУ. — 2006. — № 4. — С. 103–109 .
К блоку 7:
- Ерунова М. Г., Кадочников А. А., Якубайлик О. Э.
Геоинформационный анализ состояния природной среды государственного заповедника «Столбы» // География и природные ресурсы. — 2006. — № 2. — С. 136–142 . - Кадочников А. А., Якубайлик О. Э.
Формирование хранилища спутниковых снимков высокого разрешения на территорию Красноярского края // Тр. междунар. конф. «Вычислительные и информационные технологии в науке, технике и образовании». — Павлодар: ТОО НПФ «ЭКО». — 2006. — T. 1. — С. 541–549 . - Кадочников А. А.
Построение информационно-аналитической системы на основе геоинформационного Интернет-сервера // Материалы XXXIII междунар. конф. и IV междунар. конф. молодых ученых «Информационные технологии в науке, образовании, телекоммуникации и бизнесе». — Украина, Крым, Ялта-Гурзуф. — 2006. — С. 300–303 .
(Отделы вычислительной математики, моделирования неравновесных систем, вычислительной физики, прикладной информатики, средств телекоммуникаций и вычислительной техники)
| К началу | |
Направление 4:
Теоретические и экспериментальные исследования нелинейных процессов в механике сплошных сред
Программа 4.1:
Построение и изучение новых математических моделей в механике сплошных сред
№ гос. регистрации 0120.0 409303
Научный руководитель проекта:
д.ф.-м.н., проф. В. К. Андреев
Блок 1. 1. Исследование устойчивости горизонтального слоя жидкости со свободной границей: а) при асинхронном колебании температуры на нижней и верхней границах с учетом инверсии в распределении плотности на глубине; б) при наличии объемных источников тепла, возникающих за счет солнечной радиации. 2. Изучение воздействия высокочастотных колебаний поля внешних сил на конвекцию в смешивающихся жидкостях.
1а. В области со свободной недеформируемой поверхностью рассмотрена задача об устойчивости горизонтального слоя жидкости при колебаниях температуры на верхней и нижней границах. Граничные условия для температуры задавались в следующем виде: на верхней границе Tup = T sin(Ωt); на нижней границе Tdown = AT sin(ωΩt + ψ).
Рассмотрено влияние параметров A,ω,ψ, определяющих асинхронность колебательных режимов. Численные расчеты показывают, что значения данных параметров оказывают влияние на устойчивость слоя жидкости. Так, увеличение амплитуды колебаний температуры на нижней границе (параметр A) при малых волновых числах α приводит к повышению устойчивости. Однако обнаружено, что с ростом α наблюдается обратный эффект, когда увеличение амплитуды колебаний сокращает предел устойчивости. На рис. 7 показано влияние величины A на значение числа Рэлея Ra, при котором начинается режим неустойчивости. Здесь параметр R определен как R = (Ra - Ra0) / Ra0, где Ra0 — число Рэлея, при котором начинается режим неустойчивости при отсутствии колебаний температуры на нижней границе. На рис. 7 видно, что для α = 4 существует диапазон значений A, при которых R < 0, что свидетельствует о сокращении области устойчивости.
Влияние параметра ω, определяющего соответствие частот колебаний температуры на верхней и нижней границах, показано на рис. 8 для случая, когда α = 4 и A = 7. Увеличение частоты колебаний на нижней границе приводит к сокращению уровня воздействия, оказываемого этим параметром на устойчивость. Поэтому, как видно на рис. 8, с ростом ω значение R уменьшается.
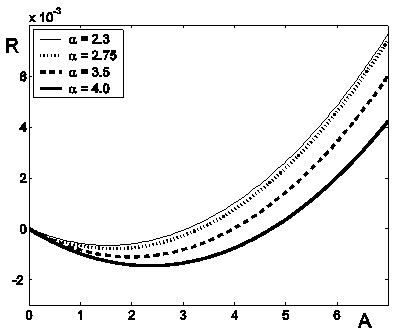
Рис. 7. Влияние параметра амплитуды колебаний A на устойчивость для различных α
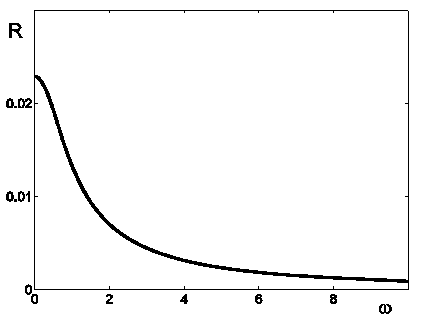
Рис. 8. Влияние параметра частоты колебаний ω на устойчивость
На рис. 9 показаны результаты, которые демонстрируют влияние параметра фазы колебаний ψ на устойчивость слоя жидкости при α = 4 и A = 4. Полученные результаты демонстрируют, что расхождение в фазах колебаний температуры на нижней и верхней границах оказывает стабилизирующее воздействие на устойчивость слоя жидкости. Как видно на рис. 9, с ростом ψ значение R увеличивается. Максимальный стабилизующий эффект достигается, когда колебания температуры находятся в противофазе при ψ = π.
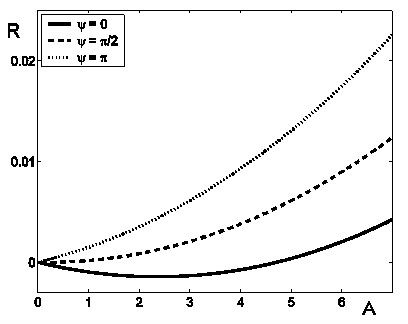
Рис. 9. Влияние параметра фазы колебаний ψ на устойчивость
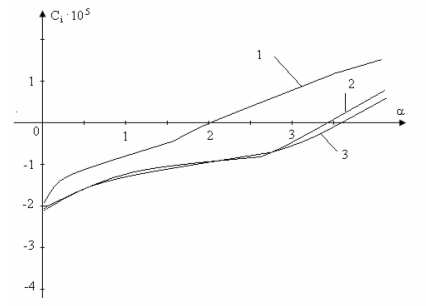
Рис. 10. Инкременты нарастания возмущений
1б. Исследована устойчивость равновесного состояния горизонтального слоя слабо сжимаемой жидкости (плотность жидкости нелинейно зависит от температуры и давления) в модели конвекции. Нижняя граница слоя — твердая стенка, верхняя — недеформируемая свободная граница. На свободной границе для функции температуры заданы граничные условия третьего рода kδθ / δn + b(θ − θgas) = Q, где Q — полный поток тепла: Q = σR + Fi + Ft. Здесь σ — числовой параметр, 0 ≤ σ ≤ 1, R — радиационный баланс свободной поверхности, Fi — потери тепла на испарение, Ft — потери тепла на конвективный теплообмен вода-воздух. В уравнении энергии учитывается функция теплового источника F = (1 − σ)Re−κz, где κ — показатель поглощения жидкости. Задача о конвекции вязкой теплопроводной жидкости рассмотрена в применении к озеру Байкал. Изучено влияние показателя поглощения и параметра σ на распределение температуры в слое. Оказалось, что чем ниже параметр поглощения κ, тем глубже проникновение солнечной радиации в среду. С ростом параметра σ внутреннее тепловыделение уменьшается.
Найдено решение, описывающее состояние механического равновесия. Устойчивость равновесия слоя жидкости изучается методом линеаризации. Показано, что состояние механического равновесия является неустойчивым. На рис. 10 приведены графики инкрементов нарастания возмущений Ci(α) = Im C(α), где α — волновое число. Вычисления проводились для различных зон Байкала с учетом характерных значений физических параметров (поток тепла, толщина слоя и др.). Кривая 1 — Северный Байкал, критическое волновое число, при котором наступает неустойчивость, α* = 2.01, критическая длина волны возмущения λ* = 881.07 м; 2 — Южный Байкал, α* = 3.42, λ* = 743.68 м; 3 — Центральный Байкал, α* = 3.58, λ* = 704.31 м.
Построены нейтральные кривые для слоя толщины 730 м (средняя глубина Байкала) при различных значениях параметра поглощения κ и числа Био Bi, характеризующего интенсивность теплообмена с окружающей средой. Найдены критические числа Рэлея.
Показано, что при уменьшении числа Био критические числа Рэлея убывают, а область неустойчивости смещается в область больших по значению волновых чисел. Полученные результаты позволяют говорить о стабилизирующем влиянии теплообмена на свободной границе. С ростом коэффициента поглощения внутреннее тепловыделение уменьшается, что приводит к увеличению зоны устойчивости.
2. Методом численного моделирования проведено исследование конвекции в бинарной жидкости, индуцируемой совместно объемными силами и воздействием высокочастотных вибрационных полей внешних массовых сил. Влияние данных факторов исследуется на основе анализа системы уравнений конвекции, полученной с помощью метода осреднений. Определяется зависимость структуры и свойств течений от начальных условий и интенсивности вибрации.
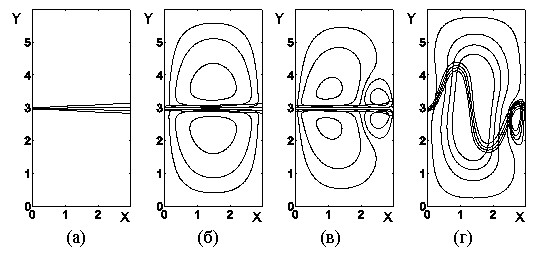
Рис. 11. Линии уровня концентрации и функции тока: (а) — начальное распределение концентрации, (б) — течение при отсутствии вибрационных сил (здесь и далее t = 740 с), (в) — вибрации направлены вдоль оси x, (г) — вибрации направлены вдоль оси y
На рис. 11 показаны результаты расчетов для случая, когда толщина переходной зоны между двумя компонентами бинарной смеси имеет линейную зависимость от координаты x, частота вибраций Ω = 60 Гц, уровень вибрации g = 0.07g0, где g0 — ускорение свободного падения. Как видно на рисунке, в случае, когда направление вибрации совпадает с осью x (рис. 11 (в)), у правой границы появляется два симметричных вихря, направление вращения которых противоположно к основным вихрям, индуцированными действием напряжений Кортевега. При этом отличия по значениям максимальной скорости наблюдается только на заключительном этапе расчета при t ≥ 800 с. В том случае, когда вибрация направлена вдоль оси y, после t = 750 с наблюдается существенная деформация переходной зоны (рис. 11 (г)). В начальный момент времени структура течения состоит из двух симметричных вихрей и подобна представленной на рис. 11 (б). С течением времени нижний вихрь постепенно увеличивает свою интенсивность, а затем за короткий промежуток времени происходит смещение центров вихрей внутрь переходной зоны и резкое увеличение максимальной скорости. Это происходит потому, что в этой конфигурации под действием вибрации происходит потеря устойчивости равновесного положения, поскольку здесь потоки массы параллельны силам плавучести.
Блок 2. Проведение группового анализа и построение инвариантных решений k- модели турбулентности в приближении пограничного слоя. Поиск инвариантов характеристик уравнений газовой динамики в лагранжевых координатах.
Выполнен групповой анализ уравнений стационарных моделей свободной турбулентности в плоском и осесимметричном случае. Построены инвариантные решения, согласующиеся с экспериментальными данными на качественном уровне.
Найдены инварианты характеристик системы уравнений одномерной газовой динамики в лагранжевых координатах и некоторые классы точных решений. С помощью нелокальных инвариантов исходная система сведена к линейному уравнению Мутара. Показана связь данного уравнения с обыкновенными дифференциальными уравнениями. Получен полный набор интегрируемых уравнений, получаемых последовательным применением двух преобразований Дарбу, с соответствующими общими решениями (О. В. Капцов, А. В. Заблуда).
Блок 3. Проведение группового анализа и построение инвариантных решений уравнений трехмерной модели смеси с плотностью, зависящей от температуры и концентрации.
С помощью группового анализа для уравнений термодиффузии установлен следующий результат. Пусть u(t, x, χ, d), p(t, x, χ, d), T(t, x, χ, d), C(t, x, χ, d), есть решение системы
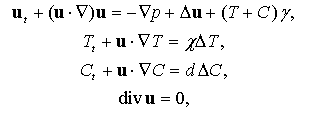
где γ = (0, 0, 1). Соответствующее решение системы уравнений термодиффузионного движения
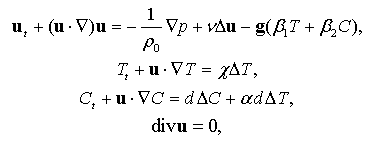
где g = (0, 0, −g), получается путем замены зависимых и независимых переменных, а также параметров χ, d по следующим формулам:
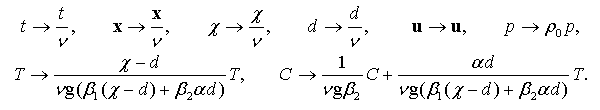
Эти формулы означают, что в решении нужно заменить t на t/ν, вместо функции p взять функцию ρ0p и т.д. Тем самым указанные преобразования эквивалентности позволяют существенно упростить исходную систему уравнений, что используется при построении инвариантных решений уравнений термодиффузии.
Блок 4. Разработка двумерной численной модели течения жидких пленок, увлекаемых спутным потоком газа.
Разработана двумерная численная модель нестационарного течения жидких пленок, увлекаемых спутным потоком газа. Проведены первые численные эксперименты по изучению формирования и эволюции нелинейных волн на границе раздела. Показано существование уединенных волн в такой системе. Проведено сравнение этих волн с гравитационно-капиллярными волнами. Показано, что при одинаковом числе Рейнольдса они имеют значительно большую амплитуду, чем гравитационно-капиллярные, а при одинаковой амплитуде — значительно меньшую фазовую скорость. При определенном масштабировании получена универсальная зависимость фазовой скорости волн на границе сдвигового течения от амплитуды (А. М. Франк).
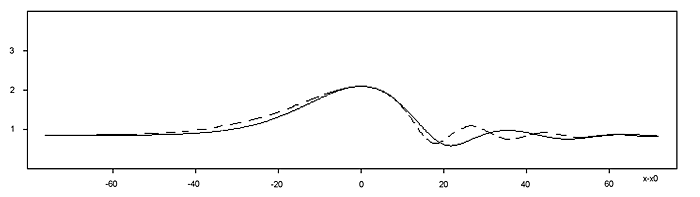
Рис. 12. Сравнение формы уединенной волны на границе раздела в сдвиговом двухфазном потоке (сплошная кривая) с гравитационно-капиллярным солитоном (пунктир) той же амплитуды
Блок 5. Разработка параллельных алгоритмов и программ для численного исследования в пространственной постановке процессов распространения упругопластических волн в сыпучих средах. Конструирование итерационных по времени и пространству алгоритмов решения многомерных динамических задач теории упругости для неоднородных сред. Численный анализ упругих фазовых деформаций в стержневых конструкциях и композиционных материалах.
На основе метода расщепления по пространственным переменным разработаны параллельные алгоритмы для численного решения трехмерных динамических задач в рамках модели несимметричной теории упругости Коссера, учитывающей независимые повороты микрочастиц материала. Выполнена программная реализация алгоритмов на отечественных многопроцессорных вычислительных системах.
Для описания геометрически нелинейного деформирования сыпучих материалов предложена математическая модель, в которой применяется тензор напряжений Коши и логарифмический тензор конечных деформаций Генки. В терминах этих тензоров сформулированы естественные ограничения на допустимое состояние сыпучей среды, вытекающие из условия прочности Мизеса-Шлейхера. Построены точные решения, описывающие простейшие однородные движения типа сдвига, сопровождающегося дилатансией материала. Построена дискретная модель пространственного движения гранулированной среды в сосуде роторного типа, совершающем круговые гармонические колебания. Численное решение задачи Коши для полученной жесткой системы обыкновенных дифференциальных уравнений реализовано с привлечением специальных методов высокой точности.
Разработаны итерационные по времени явные схемы решения трехмерных задач динамической теории упругости для неоднородных сред. Алгоритм позволяет выбирать предельно возможный для явных схем шаг по времени, обеспечивая устойчивость и монотонность решения. При программировании алгоритма применена процедура распараллеливания вычислений, существенно ускоряющая работу расчетных программ.
Дана математическая постановка проблемы об осесимметричных межфазных деформациях пластин и оболочек из сплавов с памятью формы. Проблема сформулирована как нелинейная краевая задача термоупругости с неявной зависимостью от температуры через параметр состояния, имитирующий объемную долю кристаллов новой фазы. Выполнен численный анализ задач выпучивания круговых пластин и оболочек-куполов из сплава NiTi (никелид титана) под нормальным давлением в интервале прямого фазового превращения. При малых силовых нагрузках установлен эффект интенсивного роста деформаций с увеличением объемной доли кристаллов мартенсита.
Разработано совместное применение одно- и двухсеточного моделирования для трехмерных композитов сложной формы. При анализе композитов традиционно используются микро- и макроподходы. В основе макроподхода лежат гипотезы, накладывающие определенные ограничения на поля перемещений, деформаций и напряжений. Микроподход дает возможность точно описывать поведение трехмерных композитов сложной формы, однако конечноэлементный анализ таких композитов с учетом их структуры сводится к построению дискретных базовых моделей очень высокой размерности. Предлагаемое совместное моделирование позволяет строить дискретные модели, основное достоинство которых состоит в существенном понижении размерности.
Основные публикации (по блокам).
К блоку 1:
- Гапоненко Ю. А., Вольперт В. А., Зеньковская С. М., Пойман Д. А.
Влияние высокочастотной вибрации на конвекцию в смешивающихся жидкостях // ПМТФ. — 2006. — Т. 47. — № 2. — С. 49-59. - Гапоненко Ю. А.
Конвекция в горизонтальном слое жидкости в условиях колебания температуры на свободной границе // Вестник КрасГУ. «Физико-математические науки». — 2006. — № 1. — С. 175–184 . - Андреев В. К.
Возникновение проникающей конвекции в озере Байкал // Тр. XXXVII конф. «Проблемы теоретической и прикладной. математики». — Екатеринбург: ИММ УрО РАН. — 2006. — С. 161–166 . - Бекежанова В. Б.
Об устойчивости стационарного неизотермического течения в вертикальном слое с проницаемыми границами в модели микроконвекции // Известия РАН. «Механика жидкости и газа». — 2006. — № 3.- С. 25-33. - Картошкина А. Е.
Развитие термоконцентрационного движения с плоской границей раздела // Тр. XXXVII конф. «Проблемы теоретической и прикладной математики». — Екатеринбург: ИММ УрО РАН. — 2006. — С. 205–209 . - Картошкина А. Е.
Эволюция двух несмешивающихся слоев вязкой жидкости // Вестник КрасГУ. «Физико-математические науки». — 2006. — № 1. — С. 190–194 . - Андреев В. К., Ефимова М. В.
Линеаризованная задача конвективного движения бинарной смеси с межфазной границей раздела // Вестник КрасГУ. «Физико-математические науки». — 2006. — № 1. — С. 170–174 . - Андреев В. К., Гапоненко Ю. А.
Математическое моделирование конвективных течений // Учеб. пособие. — Красноярск: КрасГУ. — 2006. — 392 с. (Рекомендовано УМС по математике и механике УМО по классическому университетскому образованию Российской Федерации). - Картошкина А. Е.
Влияние динамики на термодиффузию в плоском слое со свободными границами // Вычислительные технологии. — 2006. — Т. 11. — № 4. — С. 44-53. - Ефимова М. В.
Неустойчивость поверхности раздела при наличии термодиффузии в условиях невесомости // Вычислительные технологии. — 2006. — Т. 11. — № 1. — С. 63-69.
К блоку 2:
- Заблуда А. В.
Уравнения газовой динамики в лагранжевых координатах. Инварианты характеристик и точные решения // Вестник КрасГУ. «Физико-математические науки». -2006. — № 1. — С. 125–132 . - Капцов О. В., Ефремов И. А.
Инвариантные свойства модели дальнего турбулентного следа // Вычислительные технологии. — 2005. — Т. 10. — № 6. — С. 45-51.
К блоку 3:
- Родионов А. А.
Применение метода группового анализа к уравнениям гидродинамики // Вестник КрасГУ. «Физико-математические науки». — 2006. — № 4. — С. 142–146 . - Ryzhkov I. I.
On double diffusive convection with Soret effect in a vertical layer between co-axial cylinders // Physica D: Nonlinear phenomena. — 2006. — Vol. 215. — Is. 2. — P. 191–200 . - Рыжков И. И.
Об инвариантных решениях уравнений термодиффузий бинарной смеси в случае плоского движения // ПМТФ. — 2006. — Т. 47. — № 1. — С.95–108 . - Ryzhkov I. I.
On the normalizers of subalgebras in an infinite Lie algebra // Communications in Nonlinear Sience and Numerical Simulation. — 2006. — Vol. 11. — Is. 2. — P. 172–185 .
К блоку 4:
- Frank А. М., Kabov О. А.
Thermocapillary structure formation in a falling film: experiment and calculations // Phys. Fluids. — 2006. — Vol. 18. — 032107 (10 p.). - Франк А. М.
Термокапиллярная неустойчивость течения пленки по горизонтальной трубе // Вычислительные технологии. — 2006. — Т. 11. — Ч. 2. — С. 76-83. - Frank А. М.
Suppression of thermocapillary instability in a falling film // Phys. Fluids. — 2006. — Vol. 18. — 078106 (4 p.).
К блоку 5:
- Садовская О. В., Садовский В. М.
Параллельные вычисления в пространственных задачах динамики сыпучей среды // Вестник КрасГУ. «Физико-математические науки». — 2006. — № 1. — С. 215–221 . - Богульская Н. А., Богульский И. О., Вишняков А. А.
Имитационный подход к моделированию движения гранулированных сред // Вестник КрасГАУ. — 2005. — № 9. — С. 214–218 . - Шкутин Л. И.
Анализ плоских фазовых деформаций стержней и пластин // ПМТФ. — 2006. — Т. 4. — № 2. — С. 156–164 . - Матвеев А. Д.
Двухсеточное моделирование локально армированных трехмерных упругих тел // Вестник КрасГАУ. — 2006. — № 10. — C. 192–198 .
(Отделы вычислительных моделей в гидрофизике, дифференциальных уравнений механики, вычислительной механики деформируемых сред)
| К началу | |
Направление 8:
Проблемы деформирования и разрушения структурно-неоднородных сред и конструкций
Программа 8.3:
Физика и механика деформирования и разрушения сплошных и структурированных твердых тел, в том числе при низких и высоких температурах
№ гос. регистрации 0120.0 409301
Научный руководитель проекта:
д.т.н., проф. В. В. Москвичев
Предложена эффективная схема вероятностного моделирования предельных состояний элементов конструкций, которая предполагает последовательное решение следующих задач: исследование особенностей напряженно-деформированного состояния в области дефектов и трещин и установление их опасности; анализ развития повреждений и количественная оценка живучести; статистическое моделирование случайных параметров задачи, оценка вероятностных характеристик предельных состояний и обоснование коэффициентов запаса прочности и долговечности.
В качестве основных расчетных параметров приняты максимальные значения эквивалентных по Мизесу напряжений с учетом упрочнения материала при упругопластическом деформировании. При этом предлагается использовать следующие показатели объемности напряженного состояния:
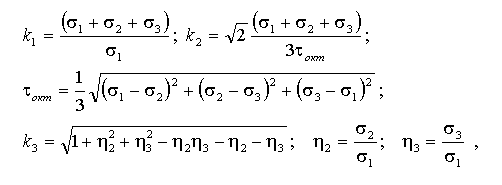
где σ1, σ2, σ3 — главные напряжения в конечном элементе в области вершины трещины, характеризующемся максимумом эквивалентных напряжений.
Характерный вид зависимостей показателей k1, k2, k3 от длины трещины представлен на рис. 14. Как вытекает из построенных графиков, рассмотренные показатели существенно отличаются по реакции на рост длины трещины. Наблюдаются максимумы коэффициентов трехосности напраженно-деформированного состояния (НДС), причем для трещин различной ориентации они соответствуют различной длине. Установлено, что коэффициенты k1 и k2 являются более чувствительными к изменениям соотношения главных напряжений.
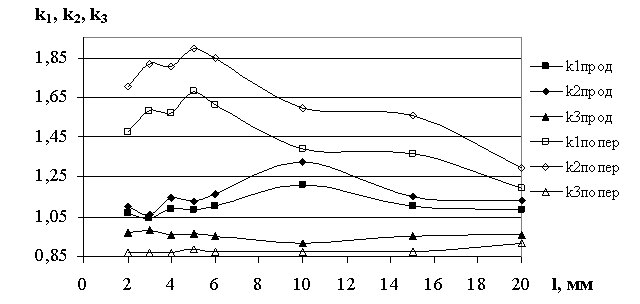
Рис. 14. Зависимости показателей k1, k2, k3 продольной и поперечной трещины
Выполненная серия расчетов и анализ полученных результатов позволили сделать выводы о том, что для оценки опасности дефектов целесообразен совместный анализ интенсивности напряжений в вершине трещины и указанных выше коэффициентов объемности напряженного состояния. Опасность дефекта (трещины) определяется преимущественно ее ориентацией в поле напряжений и особенностями структурно-механической неоднородности материала на фронте разрушения. Размер дефекта имеет меньшее значение.
Для оценки живучести и риск-анализа конструкций сложных систем разработаны расчетно-экспериментальные методы с применением CAD/CAE технологий. Необходимость развития таких методов связана с постановкой и решением нового класса задач, а именно, исследованием несущей способности и живучести конструкций в аварийных ситуациях.
Предложен укрупненный алгоритм анализа живучести и риск-анализа на основе численного моделирования НДС конструкций в аварийных ситуациях, включающий:
- поверочный расчет номинальных НДС при штатных условиях нагружения с целью установления расчетных запасов прочности и исключения из списка возможных причин грубых ошибок при проектных расчетах;
- логический анализ возможных дефектов, повреждений, перегрузок и составление перечня нештатных ситуаций с количественным обоснованием комплекса конструктивно-технологических факторов и внешних воздействий;
- расчет НДС и моделирование последовательности повреждений и разрушений для каждой нештатной ситуации; при этом выполняется многоэтапное моделирование НДС на последовательных стадиях нагружения конструкции с определением перегруженных элементов и анализом возможности наступления предельных состояний;
- сопоставление результатов моделирования напряженно-деформированных и предельных состояний с фактическими повреждениями, имевшими место в конструкции, и выбор наиболее вероятных сценариев аварий.
Методика апробирована на конкретных примерах расчетного обоснования причин и условий произошедших крупных аварий (шагающий экскаватор ЭШ-40/85, конструкция устройства обслуживания купола здания реактора атомной электростанции). Основой расчетного анализа аварийных ситуаций являлся численный (МКЭ) анализ НДС с применением CAD/CAE технологий, проведенный по разработанным в рамках данного проекта моделям и схемам (рис. 15).
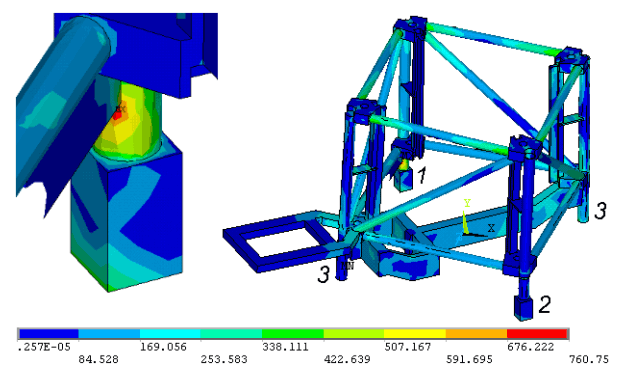
Рис. 15. Распределение интенсивности напряжений при аварийной перегрузке нижней части металлоконструкции УОК: 1 — нерегулируемая; 2 — регулируемая; 3 — нефиксируемые опоры
Разработана методика экспериментального обоснования конструктивно-технологических решений по повышению живучести узлов конструкций, включающая:
- сравнительный анализ ресурсов на стадии развития повреждений (трещин) в первоначальном и усиленном конструктивных вариантах;
- сравнительный анализ скоростей роста усталостных трещин в первоначальном и усиленном конструктивных вариантах.
В целом разработанный подход позволяет оценить эффективность модернизации конструкции с целью повышения ее живучести. Проведение модернизации целесообразно при совершенствовании узлов, разрушение которых приводит к значительным материальным потерям и потенциально опасно для окружающего персонала и смежных единиц оборудования. В связи с этим актуальной является регламентация и нормирование испытаний живучести поврежденных узлов оборудования.
Основные публикации:
- Лепихин А. М.
Концепция потенциальной зоны разрушения и задачи риск-анализа технических систем // Химическое и нефтегазовое машиностроение. — 2006. — № 6. — С. 45-48. - Доронин С. В.
Моделирование прочности и разрушения конструкций технологического оборудования // Химическое и нефтегазовое машиностроение. — 2006. — № 8. — С. 38-40. - Москвичев В. В., Доронин С. В., Гостяев В. И., Бабушкин А. В.
Численное моделирование напряженного состояния при проектировании современных крановых конструкций // Вестник машиностроения. — 2006. — № 4. — С. 3-7. - Безопасность России. Правовые, социально-экономические и научно-технические аспекты. Анализ риска и проблем безопасности. Основы анализа и регулирования безопасности / Научн. руковод. К. В. Фролов
. — М.: МГФ «Знание», 2006. — Ч. 1. — 640 с.
(Отдел машиноведения)
| К началу | |
Проект № 8.3.7 «Структурная теория пластичности и разрушения гетерогенных, волокнистых композитных материалов и конструкций»
Блок 2. «Моделирование разрушений конструкционных материалов и трещиностойкость элементов конструкций при упругопластическом деформировании».
Научный руководитель блока:
д.т.н., проф. В. В. Москвичев
Предложен метод моделирования напряженно-деформированного состояния композиционных материалов, который напрямую определяет контактные напряжения и поле перемещений, приводящий исходную задачу вычислительной механики к решению больших систем линейных алгебраических уравнений с положительно определённой матрицей, число обусловленности которой вполне приемлемо для получения численного решения на современных вычислительных системах.
Получены корректные с механической точки зрения разрешающие уравнения многослойных анизотропных оболочек вращения, непосредственно обобщающие уравнения Андреева Немировского и учитывающие не только поперечный сдвиг, но и обжатие.
Для решения возникающих линейных алгебраических систем уравнений с симметричной положительно определённой матрицей разработаны специальные методы и уточнены некоторые аспекты метода сопряжённых градиентов.
В частном случае однонаправленного волокнистого композиционного материала разработан специальный конечный элемент, поперечное сечение которого представляет собой треугольник, внутри которого расположен круг плоское поперечное сечение волокна. В результате получается краевая задача для системы обыкновенных дифференциальных уравнений большой размерности, независимой переменной в которой является осевая координата, а искомыми — контактные напряжения и перемещения. Разработаны специальные методы численного решения краевых задач такого рода на параллельных вычислительных системах.
Основные публикации:
- Чернышёва А. А., Киреев И. В.
Параллельная численная схема решения краевой задачи для одномерного эллиптического уравнения // Вестник КрасГУ. «Физико-математические науки». — 2006. — № 1. — C. 119–124 .
(Отделы вычислительной математики, машиноведения)
| К началу | |