| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2000 год
Исследования, проведенные при поддержке Российского фонда фундаментальных исследований
- Исследования, проведенные при поддержке Российского фонда фундаментальных исследований
- Проект РФФИ №
98–01–00 738 — «Исследование устойчивости инвариантных решений в новой модели микроконвекции». - Проект РФФИ №
98–05–65 280 — «Исследование проблемы прогнозирования морских природных катастроф методом обратных задач». - Проект РФФИ №
98–05–65 372 — «Теоретическое и экспериментальное исследование проблемы геоэкологической безопасности территорий на основе решения обратных задач». - Проект РФФИ №
99–01–00 453 — «Исследование термомеханических моделей динамики пластической среды при конечных деформациях». - Проект РФФИ №
99–05–64 695 — «Разработка математических моделей для исследования гидрофизических процессов в водоемах». - Проект РФФИ №
99–01–00 432 — «Бесконечные группы с различными условиями конечности». - Проект РФФИ №
00–01–00 001 — «Разработка непараметрических систем распознавания образов, основанных на методе коллективного оценивания». - Проект РФФИ №
00–01–00 893 — «Методы конечных разностей и конечных элементов повышенных порядков точности». - Проект РФФИ №
98–05–65 290 — «Математическое моделирование магнитосферных генераторов ионосферного электрического поля». - Проект РФФИ №
99–02–16 873 — «Лазерное охлаждение и локализация резонансных ионов в плазме». - Проект РФФИ и ККФН «Енисейский меридиан» №
99–07–96 013 — «Информационно-аналитическая система для управления воднобиологическими ресурсами Красноярского края». - Проект РФФИ №
00–15–96 162 — ведущие научные школы «Теория и приложения задач со свободной границей». - Проект РФФИ №
00–07–90 340 — «Создание интегрированной сети информационного центра в г. Красноярске». - Проект РФФИ №
00–01–10 094 — «Организация и проведение международной конференции «Симметрия и дифференциальные уравнения"".
Проект РФФИ №
Руководитель:
д.ф.-м.н., профессор В. К. Андреев.
Построена оптимальная система подалгебр ранга один и два для системы уравнений микроконвекции и найдены точные решения некоторых фактор-систем (А. А. Родионов).
Дан анализ устойчивости равновесного состояния в плоском слое со свободной границей и с твердыми стенками (В. К. Андреев, В. Б. Бекежанова).
Модель микроконвекции обобщена на случай неизотермической бинарной изотропной жидкой смеси с учетом эффекта термодиффузии при наличии свободных поверхностей. В рамках полученной модели в длинноволновом приближении исследована аналитически линейная монотонная неустойчивость состояния покоя плоского горизонтального слоя двухкомпонентной неизотермической жидкости между двумя параллельными твердыми стенками с учетом эффекта термодиффузии (В. Е. Захватаев).
:
- Andreev V. K.
Linearized Problem on Small Perturbations with Interface for Microgravitation Equations // Тез. докладов. «ИНПРИМ-2000». — Новосибирск: ИМ СО РАН. — 2000. — Часть II. — С. 71. - Andreev V. K., Ryabitskii E. A.
Perturbations of the Thermal Diffusion Motion of a Liquid with free Boundary // Russ. Jour. Numer. Anal. Math. Modeling. — 2000. — Vol. 15. — № 2. — P. 111–125 . - Захватаев В. Е.
Модель микроконвекции для бинарной системы. — Красноярск: ИВМ СО РАН. — 2000 (Деп. ВИНИТИ 29.02.00, № 550-В00). - Родионов А. А.
Групповой анализ одного неклассического уравнения // Тез. докладов «ИНПРИМ-2000». — Новосибирск: ИМ СО РАН. — 2000. — Часть I. — С. 17-18. - Родионов А. А.
Оптимальная система подалгебр второго порядка уравнений микроконвекции // Труды семинара «Математическое моделирование в механике». — Красноярск: ИВМ СО РАН. — 1999. — С. 120–130 (Деп. ВИНИТИ 06.06.00, № 1625–130 0).
| К началу | 2000 1999 |
Проект РФФИ №
Руководитель:
академик М. М. Лаврентьев-мл. (ИМ СО РАН).
Исполнитель от ИВМ СО РАН:
к.ф.-м.н. К. В. Симонов.
Выполнен анализ постановок основных обратных задач в проблеме цунами, имеющих целью оценки параметров источника волны и функции трассы ее распространения (К. В. Симонов).
:
- Vorob'ov A.O., Vorob'ov O.Y., Novoselov A. A., Fomin A. Y.
Spatial Tsunami Risk Models and the Problem of Insurance // The International Workshop «The Tsunami Risk Assessment Beyond 2000: Theory, Practice and Plans». Abstracts. — Moscow: IO RAS. — 2000. — P. 50. - Кирик Е. С., Симонов К. В.
Нелинейный анализ явления цунамигенности. // Тез. докладов Четвертого сибирского конгресса по прикладной и индустриальной математике. — Новосибирск: ИМ СО РАН. — 2000. — Часть II. — С. 161.
| К началу | 2000 1999 1998 |
Проект РФФИ №
Руководитель:
к.ф.-м.н. Ан. Г. Марчук (ИВМиМГ СО РАН).
Исполнитель от ИВМ СО РАН:
к.ф.-м.н. К. В. Симонов.
Выполнен вероятностный анализ каталога сильных землетрясений юга Красноярского края, получены новые данные о сейсмическом режиме региона; найденные закономерности хорошо согласуются с характеристиками сильного землетрясения, произошедшего 27 октября 2000 г. на юге-востоке края (К. В. Симонов).
:
- Марчук Ан. Г., Попов Е. А., Охонин В. А., Симонов К. В.
Графическая оболочка для визуализации и анализа сейсмической оболочки в Красноярском крае // Труды VI-ой Всероссийской конференции «Проблемы информатизации региона». — Красноярск: КГТУ. — 2000. - Marchuk An. G., Simonov K. V.
and et. all. Spatial Analysis of Tsunami Risk and Damage // The International Workshop «The Tsunami Risk Assessment Beyond 2000: Theory, Practice and Plans». Abstracts. — Moscow: IO RAS. — 2000. — P.46.
| К началу | 2000 1999 |
Проект РФФИ №
Руководитель:
д.ф.-м.н., профессор В. М. Садовский.
В рамках модели динамики сжимаемой пластической среды при конечных деформациях проведен анализ распространения волн сдвига с учетом температурного разупрочнения материала. При помощи разработанных ранее алгоритмов численной реализации динамических контактных задач выполнены расчеты косого соударения пластин с образованием периодических волн остаточных деформаций на контактной поверхности (рис. 2).
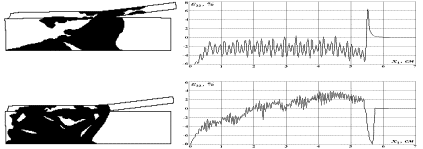
Рис. 2. Волнообразование при косом соударении пластин.
:
- Аннин Б. Д., Садовская О. В., Садовский В. М.
Численное моделирование косого соударения пластин в упругопластической постановке // Физическая мезомеханика. — 2000. — Т. 3. — № 4. — С. 23-28.
| К началу | 2001 2000 1999 |
Проект РФФИ №
Руководитель:
д.ф.-м.н., профессор В. М. Белолипецкий.
Для исследования медленных пространственных течений в стратифицированных по плотности водоемах была выбрана трехмерная гидродинамическая модель в приближениях Буссинеска, гидростатики и пограничного слоя. Разработан численный алгоритм. Расчеты пространственных течений в водоемах простой геометрии показали, что в стратифицированном водоеме можно выделить три области (верхний квазиоднородный слой, нижний и промежуточный слои), в которых формируются существенно различные картины течения. Поэтому при исследовании пространственно-временной динамики компонентов экосистемы озера необходимо учитывать качественное различие течений в рассматриваемых областях озера.
:
- Belolipetskii V. M.
Modelling of Hydrophysical Mechanisms of Impurity Transfer in Water Systems // Biodiversity and Dynamics of Ecosystems in North Eurasia. — Novosibirsk, IC&G. — 2000. — Vol. 1. — Part 2. — P. 149–151 .
| К началу | 2001 2000 1999 |
Проект РФФИ №
Руководитель:
д.ф.-м.н., профессор В. П. Шунков.
В основном завершено построение теории T0-групп. Вышла из печати монография «T0-группы». Почти слойно-конечные группы без инволюций охарактеризованы в классе смешанных групп. Для большинства спорадических групп закрыта проблема их порождаемости тремя инволюциями, две из которых перестановочны.
:
- Сенашов В. И.
Характеризация групп с обобщенно черниковской периодической частью // Мат. заметки. — 2000. — Т. 67. — Вып. 2. — С. 270–275 . - Тимофеенко А. В.
Порядки произведений инволюций в порождающих некоторые простые группы тройках элементов порядка 2 // Труды международной конференции «Симметрия и дифференциальные уравнения». — Красноярск. — 2000. — С. 215–218 . - Шунков В. П.
Т0-группы. — Новосибирск: Наука. Сибирская издательская фирма РАН. — 2000. — 198 с.
| К началу | 2001 2000 1999 |
Проект РФФИ №
Руководитель:
д.т.н., профессор А. В. Лапко.
В области математической статистики исследованы непараметрические оценки функционалов от семейства регрессий, построенных относительно некоторой системы опорных точек из экспериментальных данных. Установлено, что их асимптотические свойства в основном определяются законом распределения и количеством опорных точек и не зависят от вида регрессий. Даны приложения предложенных непараметрических коллективов в теории классификации и в теории случайных процессов. Полученные результаты обобщают традиционные непараметрические методы, основанные на оценках плотности вероятности типа Розенблатта-Парзена (А. В. Лапко, В. А. Лапко, С. В. Ченцов).
:
- Лапко А. В., Лапко В. А., Соколов М. И., Ченцов С. В.
Непараметрические системы классификации. — Новосибирск: СП «Наука». — РАН. — 1999. — 240 с. - Lapko A. V., Lapko V. A., Chentsov S. V.
Nonparametric Algorithms and Classification Systems // Pattern recognition and image analysis. — 2000. — Vol. 10. — № 1. — Р. 31-42.
| К началу | 2001 2000 |
Проект РФФИ №
Руководитель:
член-корреспондент РАН В. В. Шайдуров.
Для решения краевых задач математической физики предложен метод конечных элементов с аппроксимацией решения полиномиальными элементами, обладающими помимо традиционных степеней свободы (значения функции и ее производных в узлах интерполяции) еще и дополнительными степенями свободы — дифференциальными выражениями, связанными с оператором решаемого уравнения. Наличие таких степеней свободы повышает порядок точности решения, но не вносит дополнительных неизвестных в сеточный аналог и не повышает его числа обусловленности. В случае двухточечной краевой задачи для обыкновенного дифференциального уравнения второго порядка при повышенных порядках точности получаются трехточечные уравнения, аналогичные усеченным разностным уравнениям А. Н. Тихонова — А. А. Самарского.
Для уравнения Пуассона на прямоугольнике проведено сопоставление точности и эффективности известных схем конечных разностей и конечных элементов четвертого (повышенного) порядка точности на равномерной прямоугольной сетке для гладких и осциллирующих решений. На примере стандартной пятиточечной разностной схемы проведено сопоставление эффективности известных многосеточных итерационных алгоритмов в условиях различной гладкости точного решения.
| К началу | 2001 2000 |
Проект РФФИ №
Руководитель:
д.ф.-м.н., профессор В. В. Денисенко.
Создана математическая модель ионосферного проводника, учитывающая движение плазмы (В. В. Денисенко, С. С. Замай).
:
- Denisenko V. V., Zamay S. S.
The mathematical model of the ionospheric global conductor // «The Solar Wind — Magnetosphere System» 3. Proceedings of international Workshop. — Vienn. — 2000. — P. 363–370 .
| К началу | 2000 1999 1998 |
Проект РФФИ №
Руководитель:
д.ф.-м.н., профессор Н. Я. Шапарев.
Построена модель кинетики лазерного охлаждения плазмы с учетом неупругих столкновений и трехчастичной рекомбинации. На основании ее показано, что в охлаждаемой резонансным излучением плазме возможно образование атомов в ридберговских и автоионизационных состояниях, а также надтепловых электронов. Причем роль этих процессов в охлаждении может быть значительной.
Построена модель механического действия слабых бихроматических полей на частицы с резонансным квантовым переходом j=0 — j=1. На основании этой модели показана возможность чисто оптического конфаймента сгустков ультрахолодной плазмы (с резонансными ионами) в поле взаимно-ортогональных бихроматических стоячих волн.
:
- Gavrilyuk A. P., Krasnov I. V., Shaparev N. Ya.
Laser Cooling of Rarefied Plasma with Resonant Ions // Proceeding of the 5-th Russian-Chinese Symposium on Laser Physics and Laser Technology. — Tomsk. — 2000. — P. 6-12. - Gavrilyuk A. P., Krasnov I. V., Polyutov S. P., Shaparev N. Ya.
About a Possibility of Ultracold Plasma Optical Confinement in Weak Bichromatic Laser Fields // Proceeding of the 5-th Russian-Chinese Symposium on Laser Physics and Laser Technology. — Tomsk. — 2000. — P. 56-59.
| К началу | 2001 2000 1999 |
Проект РФФИ и ККФН «Енисейский меридиан» №
Руководитель:
к.э.н. Н. Г. Шишацкий (Красноярский отдел института экономики и организации промышленного производства СО РАН).
Участники от ИВМ СО РАН:
В. С. Филимонов, С. С. Замай, О. Э. Якубайлик.
Получены необходимые топоосновы (цифровые карты) для реализации проекта. Проведены работы по включению в таблицы и базы данных информации о первичных оптических характеристиках и связанных с ними параметрах, определяющих качество вод. В рамках проблемы изучения глобального круговорота углерода выполнена оценка стока органического углерода в р. Енисей (В. С. Филимонов).
Разработаны подходы к описанию динамики водно-биологических ресурсов бассейна реки Енисей с помощью балансовых моделей распределения потоков на графах (Б. А. Елгин.). Созданы основные компоненты ГИС-приложения, позволяющие работать с базой данных атрибутивной информации (С. А. Ковязин, В. В. Касьянов), отображать их характеристики на фоне картографической информации, задавать параметры модели и выбирать различные режимы расчета динамики ресурсов (Б. А. Елгин, К. В. Теплицкий., О. Э. Якубайлик).
:
- Филимонов В. С., Апонасенко А. Д.
Оценка сброса органического углерода и взвешенных веществ по р. Енисей с помощью оптических методов // Материалы Международной научной конференции «Фундаментальные проблемы воды и водных ресурсов на рубеже третьего тысячелетия». — Томск. — 2000. — С. 359–361 .
| К началу | |
Проект РФФИ №
Руководитель:
член-корреспондент РАН В. В. Пухначев.
Аналитическими и численными методами построены некоторые инвариантные решения осесимметрических термокапиллярных течений (В. К. Андреев).
Выполнен групповой анализ одного неклассического уравнения неоднородной жидкости и найдены точные решения, описывающие движения со свободной границей (А. А. Родионов).
В рамках модели микроконвекции аналитически исследована в длинноволновом приближении линейная монотонная неустойчивость состояния покоя плоского горизонтального слоя двухкомпонентной неизотермической жидкости между двумя параллельными твердыми стенками с учетом эффекта термодиффузии.
Определены границы линейной монотонной неустойчивости Бенара-Марангони состояния механического равновесия плоского горизонтального слоя с деформируемой поверхностью; показано, что для коротковолновой моды конвекции рассматриваемый эффект может ощутимо понизить наименьшие критические числа Марангони по сравнению с результатами, полученными с использованием приближения Буссинеска (В. Е. Захватаев).
:
- Адмаев О. В., Андреев В. К.
Моделирование осесимметрических термокапиллярных течений // Труды семинара «Математическое моделирование в механике». — Красноярск: ИВМ СО РАН. — 1999. — С. 10-22 (Деп. ВИНИТИ 06.06.00, № 1625–130 0). - Захватаев В. Е.
Длинноволновая термокапиллярная неустойчивость плоского слоя с учетом эффекта теплового расширения жидкости // Тезисы докладов. VII-го Российского симпозиума «Механика невесомости. Итоги и перспективы фундаментальных исследований гравитационно-чувствительных систем». — Москва. — 2000. — С. 36-37. - Родионов А. А.
Групповой анализ одного неклассического уравнения // Тезисы докладов «ИНПРИМ-2000». — Новосибирск: ИМ СО РАН. — 2000. — Часть I. — С. 17-18.
| К началу | 2001 2000 |
Проект РФФИ №
Руководитель:
член-корреспондент РАН В. В. Шайдуров.
При активном участии сотрудников Института создана Концепция краевой целевой программы «Информатизация Красноярского края до 2005 года». Она содержит анализ состояния информатизации в Красноярском крае, цели информатизации до 2005 года, методы и средства их достижения. Главный акцент делается на интеграцию материальных, финансовых, интеллектуальных и организационных ресурсов, на выработку общекраевых стандартов, принципов, правил и протоколов, а также на мотивацию их использования и интеграции. Концепция утверждена губернатором Красноярского края и принята к реализации.
В течение 2000 года в Красноярском научном центре СО РАН модернизировалось компьютерное и телекоммуникационное оборудование, приобретено и написано программное обеспечение для создания распределенной библиотечной сети на основе международных стандартов ISIS и сетевых протоколов Z39.50. В настоящий момент эта сеть находится в опытной эксплуатации и объединяет 5 библиотек институтов и Центральную научную библиотеку КНЦ СО РАН.
| К началу | 2001 2000 |
Проект РФФИ №
Председатель конференции:
член-корр. РАН Ю. Н. Павловский.
Зам. председателя: д.ф.-м.н., профессор В. К. Андреев.
Конференция «Симметрия и дифференциальные уравнения» успешно проведена с 21 по 25 августа 2000 года. Издан сборник тезисов докладов участников конференции.
| К началу | |