| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2011 год
Гранты российских научных фондов
- Гранты РФФИ
- Грант РФФИ №
09–01–00 395-а — «Условия конечности в бесконечных группах» - Международный проект РФФИ №
09–05–91 000-АНФ_а (Российско-Австрийский) — «МГД аспекты «флэппинг» колебаний токового слоя магнитосферного хвоста» - Грант РФФИ
10–01–00 509 «Группы с конечным числом элементов» - Проект РФФИ №
11–01–00 053 — «Численное моделирование термомеханических процессов в средах с микроструктурой на суперкомпьютерах» - Грант РФФИ №
11–01–00 106-а «Численное моделирование динамических процессов в больших электрических сетях» - Грант РФФИ №
11–01–00 283-а — «Структуры и устойчивость течений сопряженных задач тепломассообмена» - Грант РФФИ №
11–01–00 224 — «Метод траекторий и конечных элементов для решения уравнений Навье-Стокса для вязкого теплопроводного газа» - Грант РФФИ №
11–04–98 089-р-Сибирь «Оценка и прогноз вклада бореальных лесов Восточной Сибири в глобальный круговорот углерода» - Грант РФФИ №
11–01–06 079-г — «Организация и проведение XIX Всероссийского семинара «Нейроинформатика, её приложения и анализ данных» - Грант РФФИ №
11–01–06 080-г — «Организация и проведение XIV Всероссийского семинара «Моделирование неравновесных систем» - Грант РФФИ №
11–01–09 322_моб_з — «Участие в работе Международной конференции «Математические и информационные технологии, MIT-2011» - Грант РФФИ №
11–01–09 326_моб_з — «Участие в работе Международной конференции «Математические и информационные технологии, MIT-2011» - Грант РФФИ
11–07–09 255_моб_з — «Участие в работе Международной конференции «Математические и информационные технологии, MIT-2011» - Грант РФФИ №
11–01–09 321_моб_з — «Участие в международной конференции Европейской ассоциации исследований при пониженной гравитации» - Грант РФФИ
11–07–16 020-моб_з_рос — «Участие в международной конференции «Технологии разработки информационных систем (ТРИС-2011)» - Гранты Красноярского краевого фонда поддержки науки и научно-технической деятельности
Гранты РФФИ
Грант РФФИ №
Руководитель: д.ф.-м.н., проф. В. П. Шунков
Изучались группы Шункова с условием, что нормализатор любой конечной нетривиальной подгруппы обладает почти слойно конечной периодической частью. При этом условии установлена почти слойная конечность периодической части группы Шункова с сильно вложенной подгруппой, обладающей почти слойно конечной периодической частью. Получены новые свойства почти слойно конечных групп. Доказан критерий почти слойно конечности группы. Изучено строение конечных силовских 2-подгрупп в группах Шункова с условием, что нормализатор любой нетривиальной конечной подгруппы обладает почти слойно конечной периодической частью. Получен признак непростоты бесконечной группы, не содержащей групп кватернионов, но содержащей Mp-группу.
На базе алгебраических и компьютерных моделей простых правильногранных тел классифицированы все выпуклые многогранники, каждая грань которых либо составлена из двух правильных многоугольников, либо является правильным многоугольником. Описан алгоритм «склеивания» графов правильногранников по одинаковым граням. А. В. Тимофеенко создан и размещен в интернете «Атлас выпуклых правильногранников», где каждый из правильногранников обладает правильными и составленными из правильных многоугольников гранями. Явно указаны (2 x 2, 2)-тройки инволюций в знакопеременных группах степени некоторых конечных простых групп.
Основные публикации:
- Сенашов В. И.
Строение конечных силовских подгрупп в некоторых группах Шункова // Тез. докл. междунар. конф. по алгебре и геометрии. — Екатеринбург: УМЦ-УПИ. — 2011. — С. 149–151 . - Сенашов В. И.
Силовские 2-подгруппы в некоторых группах Шункова // Тез. докл. междунар. конф. по алгебре и мат. логике. — Казань: КФУ. — 2011. — 161–162 . - Сенашов В. И.
Строение силовских подгрупп в некоторых группах Шункова // Тез. докл. междунар. конф. «Мальцевские чтения». — Новосибирск. — 2011. — С. 82. - Козулин С. Н., Сенашов В. И., Шунков В. П.
Mp-группы, не содержащие групп кватернионов. Препринт № 3-11. — Красноярск: ИВМ СО РАН. — 2011. — 15 с. - Сенашов В. И.
2-подгруппы в некоторых группах Шункова // Тез. докл. VIII Междунар. конф. «Алгебра и теория чисел: современные проблемы и приложения». — Саратов: Саратовский ун-т. — 2011. — С. 67. - Тимофеенко А. В.
К перечню выпуклых правильногранников // В сб.: «Современные проблемы математики и механики и их приложения». — М.: МГУ. — 2011. — Т. VI. — Математика. — Вып. 3. — С. 148–163 .
(Отдел дифференциальных уравнений механики)
| К началу | |
Международный проект РФФИ №
Руководитель: д.ф.-м.н., проф. Н. В. Еркаев
Численно исследована линейная МГД «флэппинг» неустойчивость токового слоя в трехмерной постановке задачи для сжимаемой плазмы. Профиль тангенциальной компоненты магнитного поля моделируется гиперболической функцией, описывающей вариацию поля типа Харриса поперек токового слоя. Разложение по Фурье-гармоникам в направлении фонового электрического тока позволяет свести исходную трехмерную задачу к двумерной. Конечно-разностная численная схема Лакса-Вендрофа применяется для расчета временной эволюции малых начальных возмущений магнитного поля, плотности, скорости и давления. Данная работа представляет собой расширенное численное исследование так называемой неустойчивости «двойного градиента», являющейся возможным генератором наблюдаемых флэппинг колебаний в токовом слое магнитосферного хвоста. Данные колебания исследовались ранее в рамках упрощенной квази-одномерной аналитической модели для несжимаемой плазмы. Получена дисперсионная зависимость инкремента неустойчивости от волнового числа для изгибной моды, которая хорошо согласуется с аналитической теорией. Исследована зависимость неустойчивости от нормальной компоненты магнитного поля.
Основные публикации:
- Korovinskiy D. B., Ivanova V. V., Erkaev N. V., Semenov V. S., Ivanov I. B., Biernat H. K., Zellinger M.
Kink-like mode of a double gradient instability in a compressible plasma current sheet // Advances in Space Research. — 2011. — V. 48 . — P. 1531–153 6. — doi: 10.1016/j.asr.2011.07.008. - Сасунов Ю. Л., Семенов В. С., Еркаев Н. В., Хейн М. Ф., Бирнат Х. К.
Асимметричное магнитное пересоединение: Сравнение результатов МГД моделирования с аналитическим решением // Вестник СПбГУ. — 2011. — № 4. — Вып. 2. — С. 88-95.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ
Руководитель: д.ф.-м.н., профессор А. И. Созутов (СФУ), ответственный исполнителm от ИВМ СО РАН: В. И. Сенашов
Получены новые свойства почти слойно конечных групп. Доказан критерий почти слойно конечности группы. Изучено строение конечных силовских 2-подгрупп в группах Шункова с условием: нормализатор любой нетривиальной конечной подгруппы обладает почти слойно конечной периодической частью.
Основные публикации:
- Сенашов В. И.
Строение конечных силовских подгрупп в некоторых группах Шункова // Тез. докл. междунар. конф. по алгебре и геометрии. — Екатеринбург: УМЦ-УПИ. — 2011. — С. 149–151 . - Сенашов В. И.
Силовские 2-подгруппы в некоторых группах Шункова // Тез. докл. междунар. конф. по алгебре и мат. логике. — Казань: КФУ. — 2011. — 161–162 . - Сенашов В. И.
Строение силовских подгрупп в некоторых группах Шункова // Тез. докл. междунар. конф. «Мальцевские чтения». — Новосибирск. — 2011. — С. 82. - Козулин С. Н., Сенашов В. И., Шунков В. П.
Mp-группы, не содержащие групп кватернионов. Препринт № 3-11. — Красноярск: ИВМ СО РАН. — 2011. — 15 с. - Сенашов В. И.
2-подгруппы в некоторых группах Шункова // Тез. докл. VIII Междунар. конф. «Алгебра и теория чисел: современные проблемы и приложения». — Саратов: Саратовский ун-т. — 2011. — С. 67.
(Отдел дифференциальных уравнений механики)
| К началу | |
Проект РФФИ №
Руководитель: д.ф.-м.н., проф. В. М. Садовский
Разработаны программные приложения в системе CUDA для численного исследования процессов распространения плоских продольных волн в слоистых средах с вязкоупругими прослойками на графических высокопроизводительных системах. В расчетах одномерной задачи о распространении плоских продольных волн в слоистой среде обнаружены медленные волны маятникового типа, которые возникают в результате многократного переотражения волн от тонких прослоек.
На рис. VI.1 приведены зависимости безразмерной скорости частиц от пространственной координаты, отнесенной к толщине слоя, в задаче о действии $\Lambda $-образного импульса давления. Импульс единичной амплитуды действовал на левой границе расчетной области, правая ее граница считалась неподвижной. Результаты демонстрируют качественное отличие волновой картины в слоистых средах по сравнению с однородной средой. Это отличие на начальном этапе заключается в появлении отраженных от прослоек волн — характерных осцилляций за фронтом волны нагружения по мере ее прохождения через границы раздела. Со временем, после многократного переотражения за фронтом головной волны возникает стационарная волновая картина, так называемая волна маятникового типа.
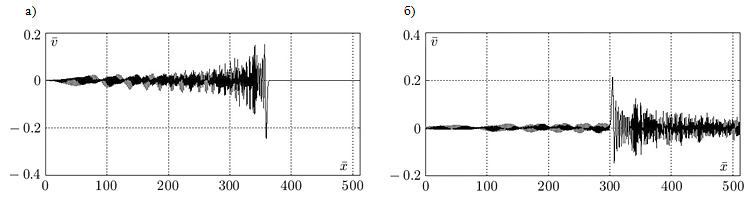
Рис. VI.1. Распределение скорости за фронтом падающей (а) и отраженной (б) волн, вызванных в слоистой среде воздействием короткого импульса
Разработана нелинейная термомеханическая модель среды с микроструктурой, учитывающая в рамках теории конечных деформаций вращательные степени свободы частиц. Система уравнений для описания нелинейных волн деформации и поворота частиц приведена к самосогласованной системе законов сохранения, что гарантирует гиперболичность системы и позволяет применить к ее исследованию эффективные численные методы, адаптированные к расчету обобщенных решений с разрывами, вызванными сосредоточенными и импульсными воздействиями. Аналогичная форма получена для системы нелинейных уравнений динамики редуцированного континуума с равным нулю тензором моментных напряжений. На этой основе найден общий вид математически корректной постановки начальных и граничных условий, а также условий симметрии при решении краевых задач.
Основные публикации:
- Садовский В. М.
Об условиях выпуклости изотропной функции от тензора второго ранга // Журнал СФУ. Серия: математика и физика. — 2011. — Т. 4. — № 2. — С. 265–272 . - Садовский В. М.
Термодинамически самосогласованная система законов сохранения несимметричной теории упругости // Дальневосточный математический журнал. — 2011. — Т. 11. — № 2. — С. 201–212 . - Красненко А. Н., Садовская О. В.
Математическое моделирование сдвиговых течений сыпучей среды с застойными зонами // Тр. всерос. науч. конф. «Фундаментальные и прикладные вопросы механики и процессов управления». — Владивосток: ИАПУ ДВО РАН. — 2011. — С. 91-96. - Енавин А. В., Садовский В. М.
Математическое моделирование осаждения частиц золота при движении фильтрационного потока через отвал // Тр. всерос. науч. конф. «Фундаментальные и прикладные вопросы механики и процессов управления». — Владивосток: Ин-т автоматики и процессов управления ДВО РАН. — 2011. — С. 340–345 .
(Отдел вычислительной механики деформируемых сред)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., профессор Е. А. Новиков
Разработан программный модуль среды ИСМА для исследования режимов электрических машин. Рассмотрены вопросы численного моделирования динамических систем в электроэнергетических системах как элемент стратегического управления. Изучены примеры численного анализа динамики процессов в электромеханической системе. Построена математическая модель процесса разгона и движения электроподвижного состава с реостатно-контакторным управлением. Разработан алгоритм интегрирования уравнений движения, выбор шага в котором осуществляется по точности и устойчивости. Создан алгоритм переменного порядка и шага на основе явного трехстадийного метода типа Рунге-Кутты Построен метод типа Розенброка первого порядка для решения дифференциально-алгебраических задач, который применен для расчета RC-цепей. Построен (3, 2)-метод третьего порядка точности с переменным шагом интегрирования, который применен для моделирования кольцевого модулятора.
Основные публикации:
- Новиков Е. А., Уатай Б. У.
Численное моделирование RC-цепей L-устойчивым методом первого порядка точности // Вестник КрасГАУ. — 2011. — №1. — С. 17-22. - Novikov E. A.
(2,1)-method for solving stiff nonautonomous problems // Automation and Remote Control. — 2011. — V. 72 (11). — P. 345–351 . - Новиков Е. А., Захаров Ю. А.
Согласование областей устойчивости в явном трехстадийном методе типа Рунге-Кутта // Вестник ТюмГУ. — 2011. — № 7. — С. 187–192 . - Новиков Е. А.
Алгоритм переменного порядка и шага на основе явного трехстадийного метода типа Рунге-Кутта // Известия Саратовского ун-та. Серия: Математика. Механика. Информатика. — 2011. — Т. 11. — Вып. 3. — Ч. 1. — С. 46-53. - Новиков Е. А.
Численное моделирование кольцевого модулятора (3,2)-методом решения жестких задач // Информатика и системы управления. — 2011. — № 1(27). — С. 50-61. - Ващенко Г. В., Новиков Е. А.
Параллельный вариант явного метода Рунге-Кутта с контролем точности вычислений // Приложение к «Вестнику КрасГАУ». «Ресурсосберегающие технологии». — Красноярск. — 2011. — № 7. — С. 84-88. - Новиков Е. А., Уатай Б. У.
Численное моделирование кольцевого модулятора методом Розенброка первого порядка // Приложение к «Вестнику КрасГАУ». «Ресурсосберегающие технологии». — Красноярск. — 2011. — № 7. — С. 88-93. - Шорников Ю. В., Новиков Е. А.
Моделирование гибридных систем L-устойчивым методом в инструментальной среде ИСМА // Приложение к «Вестнику КрасГАУ». «Ресурсосберегающие технологии». — Красноярск. — 2011. — № 7. — 103–108 .
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., профессор В. К. Андреев
1. Исследована задача об устойчивости механического равновесия многокомпонентной смеси в плоском слое, подогреваемом сверху/снизу в поле силы тяжести. Учитываются перекрестная диффузия и эффект Соре. В основном состоянии движение отсутствует, при этом постоянный градиент температуры в слое приводит к возникновению постоянных градиентов концентрации компонентов благодаря эффекту Соре. Рассматриваемая задача является обобщением известной задачи Рэлея — Бенара об устойчивости механического равновесия в плоском слое однородной жидкости, подогреваемой снизу.
С помощью специальных преобразований задача об устойчивости сведена к задаче без перекрестной диффузии и эффекта Соре (исключаются соответствующие члены в уравнениях). Рассмотрено несколько вариантов граничных условий на горизонтальных стенках: 1) свободные, проницаемые для вещества границы 2) твердые, проницаемые для вещества границы 3) твердые, непроницаемые для вещества границы. Случай проницаемых границ соответствует постоянным значениям концентрации на границах, а случай непроницаемых границ — отсутствию потока вещества через границы. Для граничных условий типа 1 и 2 доказаны теоремы, обобщающие принцип монотонности возмущений (или принцип обращения устойчивости) на случай многокомпонентной смеси с эффектом Соре. Эти теоремы позволяют оценить область устойчивости системы в пространстве параметров. Для граничных условий типа 1 получена явная формула для критических чисел Рэлея. Задача с граничными условиями типа 3 решалась численно для случая трехкомпонентной смеси. Построены нейтральные кривые и карты устойчивости в пространстве параметров задачи. Проведено сравнение результатов для различных типов условий на границах слоя.
На рис. VI.2 приведены карты областей неустойчивости для тройной смеси на плоскости ($\Psi $, $\psi $${}_{1}$), где $\Psi $ — полное отношение разделения смеси, а $\psi $${}_{1}$ — отношения разделения первого компонента (эти параметры характеризуют эффект термодиффузии компонентов смеси, при этом $\psi {}_{2} = \Psi -\psi {}_{1}$). Рассматривается случай твердых, непроницаемых для вещества границ при подогреве снизу. Области неустойчивости меняют свою структуру в зависимости от отношения чисел Шмидта, которые характеризуют диффузионные свойства компонентов смеси.
2. Исследована устойчивость двухслойного течения Марангони - Пуазейля с недеформируемой границей раздела в наклонном канале относительно пространственных возмущений. Канал ограничен неподвижными твердыми стенками, вдоль которых температура меняется по линейному закону и описывается обобщенным решением Остроумова - Бириха. Условием существования такого обобщенного решения является равенство $\rho _{1} \beta _{1} =\rho _{2} \beta _{2} $, где $\rho _{j} $, $\beta _{j} $ — плотность и коэффициент теплового расширения $j$-ой ($j=1,\, 2$) жидкости соответственно, существенно ограничивающее класс жидкостей, для которых реализуется подобное течение.
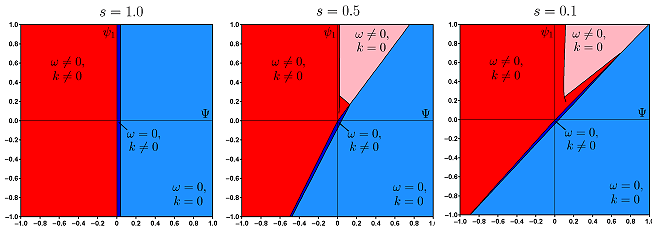
Рис. VI.2. Области монотонной и колебательной неустойчивости на плоскости ($\textit{$\Psi $, $\psi $${}_{1}$}$) для различных значений отношения чисел Шмидта $\textit{s}$ = Sc${}_{11}$/Sc${}_{22}$. Число Прандтля Pr = 10, число Шмидта Sc${}_{22}$ = 1000. Обозначения: $\textit{$\omega $}$ — частота колебаний, $\textit{k}$ — волновое число в направлении оси $\textit{x}$
Спектральная задача о малых пространственных возмущениях обобщенного решения не сводится к двумерной, поскольку не допускает преобразования Сквайра. Для характеристики пространственных возмущений вводится параметр $\lambda =\mu _{1} /\mu $, где $\mu ^{2} =\mu _{1}^{2} +\mu _{2}^{2} $ — модифицированное волновое число, $\mu _{1} $, $\mu _{2} $ — волновые числа вдоль осей соответствующих направлений. Значение $\lambda =1$ соответствует плоским возмущениям ($\mu _{2} =0$), а $\lambda =0$ — возмущениям с $\mu _{1} =0$, не зависящим от продольной координаты, и представляющим собой стационарные валы, оси которых ориентированы в направлении основного течения («спиральные возмущения»). Дополнительным определяющим параметром является величина $\theta $, по величине которой можно судить о характере нагрева стенок: при $\theta >1$ верхняя стенка канала горячее, $\theta <1$ — нижняя. В случае, когда $\theta <1$, имеет место смена режимов неустойчивости (рис. VI.3).
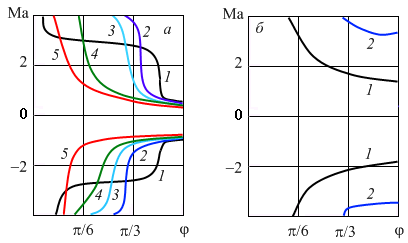
Рис. VI.3. Зависимость минимальных критических чисел Марангони от угла наклона системы:
(а) — $\theta <1$, (б) — $\theta >1$. Кривые 1-5 — $\lambda =1,\, \, 0.7,\, \, 0.5,\, \, 0.2,\, \, 0$
Положительным значениям числа Марангони соответствует случай, когда стенки канала нагреваются в направлении оси $Ox$, отрицательным — когда стенки охлаждаются. В области $0\le \varphi \le \varphi _{*} $ ($\varphi $ — угол отклонения системы от горизонтали) наиболее опасными являются плоские возмущения. При дальнейшем увеличении угла наклона происходит переход от плоской формы неустойчивости к спиральной. Критическое число Марангони $Ma_{m}$ достигается при $\lambda =0$ для любых углов $\varphi _{*} <\varphi <\pi /2$.
С ростом числа Грасгофа (фактически это означает увеличение толщины второго слоя или температуры нижней стенки при заданном постоянном градиенте температуры) область значений $\varphi$, в которой наиболее опасными являются плоские возмущения, расширяется (табл. VI.1).

Таблица VI.1. Критический угол наклона системы в зависимости от числа
Кризис, вызванный пространственными возмущениями, связан с неустойчивой температурной стратификацией. При $\theta >1$ стратификация является потенциально устойчивой, и в этом случае неустойчивость связана с развитием плоских гидродинамических возмущений (рис. VI.3 б).
Поскольку среди пространственных возмущений наиболее опасными являются спиральные, то, полагая $\mu _{1} =0$ в полной спектральной задаче, получим соответствующую задачу для возмущений этого вида, результаты решения которой позволяют определить характер неустойчивости. Для углов наклона, близких к критическим $\varphi _{*}^{\pm } $, возникает неустойчивость монотонного вида (рис. VI.4), от нейтральной кривой колебательной неустойчивости 3 «отцепляется» монотонная мода. С ростом числа Грасгофа критическое волновое число $\mu _{2}^{*} $ также возрастает. Пара близко расположенных кривых 1 (рис. VI.4, б) соответствует двум уровням неустойчивости, которые возникают при больших числах Грасгофа.
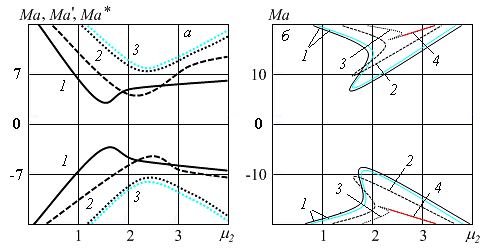
Рис. VI.4. Нейтральные кривые:
(а) — $\varphi =\pi /3$, $\textit{1}$ — $Gr=4.78\cdot 10^{-6} $, $Ma^{*}=Ma\cdot 10^{-2} $; 2 — $Gr=4.78\cdot 10^{-3} $, Ма; 3 — $Gr=4.78\cdot 10^{3} $, $Ma'=Ma\cdot 10^{4} $;
(б) — $Gr=4.78\cdot 10^{3} $, $Ma'=Ma\cdot 10^{4} $, 1,2 — $\varphi =\pi /3,\, \, \pi /4$, $\textit{3,4}$ — $\varphi =\pi /5$.
Кривые $\textit{1-3}$ соответствуют колебательной неустойчивости, $\textit{4}$ — монотонной
Анализ собственных функций показывает, что в результате развития спиральных возмущений в системе с малым отклонением от горизонтали возникают два вихря с одинаковым направлением циркуляции, прилегающих к верхней и нижней стенкам канала, между которыми образуется вихрь противоположной циркуляции. В системе с углом наклона, близким к критическому $\varphi _{*}^{\pm } $, могут возникать два (при малых числах Грасгофа) или четыре (при больших $Gr$) вихря с противоположными направлениями циркуляциями. В первом случае вихри расположены один над другим и локализованы в средней части канала, а во втором — по два вихря в каждом слое — один у стенки, другой у границы раздела.
3. Рассмотрена задача об однонаправленном двухслойном течении в плоском слое, ограниченном твердыми стенками, при отсутствии силы тяжести. На внешних границах задано линейное распределение температур. Поверхность раздела $\Gamma $ предполагается плоской и недеформируемой, на ней коэффициент поверхностного натяжения линейно зависит от температуры. Источниками движения вязкой теплопроводной жидкости являются термокапиллярный эффект, градиент давления и движение одной из границ. Меняя скорость движения стенки, градиенты давления и температуры, можно получать различные режимы течений. Подбирая градиент температуры $A$, можно добиться, чтобы градиент давления $\bar{a}=0$ был нулевым. Получающееся течение (с постоянным давлением в слоях) является суперпозицией термокапиллярной конвекции и сдвигового течения Куэтта, обусловленного движением границы, и описывается решением типа Остроумова - Бириха. С изменением скорости движения стенки (Re$\textit{ — }$число Рейнольдса, отрицательным значениям соответствует случай, когда направление движения стенки противоположно направлению продольной оси), толщин слоев ($h_{1}, \, \, h_{2}, \, \, h=h_{1} /h_{2} $) и градиентов температуры (Ma$\textit{ — }$число Марангони, отрицательным значениям соответствует случай, когда направление градиента температуры противоположно направлению продольной оси) происходит изменение профиля скорости (рис. VI.5).
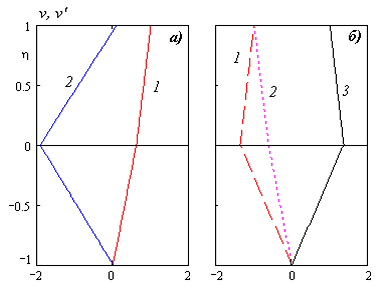
Рис. VI.5. Безразмерное распределение скорости жидкостей в слоях при изменении h, Ma, Re:
а) 1 — $h=0.1$, $\, {\rm Ma}=2.235\cdot 10^{4}, \, $$Re=5.408\cdot 10^{3} $, $v$, 2 — $h=10$, $\, {\rm Ma}=2.235\cdot 10^{8}, \, $$Re=5.408\cdot 10^{5} $, $v'$;
б) $h=0.1$, 1 — $\, {\rm Ma}=2.235\cdot 10^{4}, \, $$Re=-5.408\cdot 10^{3} $, 2 — $\, {\rm Ma}=-2.235\cdot 10^{4}, \, $$Re=-5.408\cdot 10^{3} $, 3 — $Re=5.408\cdot 10^{5} $, $\, {\rm Ma}=-2.235\cdot 10^{4} $
В рамках линейной теории исследована устойчивость указанного течения относительно плоских возмущений. Найдена длинноволновая асимптотика комплексного декремента и получены аналитические представления собственных функций.
В зависимости от толщин слоев и величины их отношения $\textit{h }$наиболее опасным становится тип неустойчивости, связанный с развитием стоячих (монотонных) или бегущих (колебательных) тепловых возмущений. Если $h_{1}, \, \, h_{2} \, >1$, то наиболее опасными являются монотонные возмущения (сплошные кривые на рис. VI.6, б). При малых толщинах слоев имеет место смена режимов неустойчивости с монотонного на колебательный (штриховые линии).
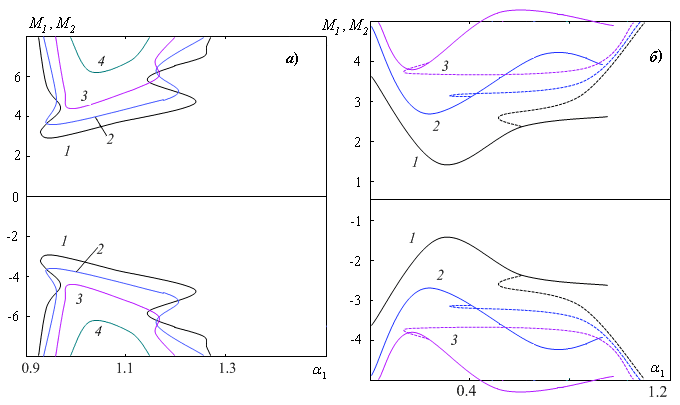
Рис. VI.6. Нейтральные кривые при
а) гидродинамические моды: $\textit{1-4}$ — $h=10^{3}, \, \, 10^{2}, \, \, 1,\, \, 10^{-2} $, $M_{1} ={\rm Ma}\cdot 10^{2} $, $M_{2} ={\rm Ma}\cdot 10^{3} $ при $h=\, 10^{-2} $;
б) тепловые моды при: $\textit{1-3}$ — $h=10^{3}, \, \, 1,\, \, 10^{-2} $, $M_{1} ={\rm Ma}\cdot 10,$ $M_{2} ={\rm Ma}\cdot 10^{2} $ при $h=10^{-2} $
Основные публикации:
- Gaponenko Y., Mialdun A., Shevtsova V.
Interfacial shear stress in gas-liquid flow in annuli // J. Multi Phase Flow. — 2011. — doi:10.1016/j.ijmultiphaseflow.2011.09.005. - Gaponenko Yu., Nepomnyashchy A. and Shevtsova V.
Thermocapillary and shear driven flows in gas/liquid system in annular duct // Journal of Physics: Conference Series. (In press). - Ryzhkov I. I.
Thermocapillary instabilities in liquid bridges revisited // Bulletin of the European Low Gravity Research Association. — 2011. — V. 27. — P. 46-47. - Рыжков И. И.
О термокапиллярной неустойчивости в жидком цилиндре // Тез. докл. всерос. конф. «Задачи со свободными границами: теория, эксперимент и приложения». — Новосибирск. — 2011. — С. 86-87. - Рыжков И. И.
О термокапиллярной неустойчивости жидкого цилиндра, обдуваемого потоком газа // Тез. докл. междунар. конф. «Современные проблемы прикладной математики и механики: теория, эксперимент, практика». — Новосибирск. — 2011. — C. 101. - Андреев В. К., Бекежанова В. Б.
О малых возмущениях термокапиллярного стационарного двухслойного течения в плоском слое с подвижной границей // Журнал СФУ. Серия: математика и физика. — 2011. — № 4(4). — С. 434–444 . - Бекежанова В. Б.
О смене форм неустойчивости стационарного течения двухслойной жидкости в наклонном канале // МЖГ. — 2011. — № 4. — С. 24-34. - Бекежанова В. Б.
О пространственных возмущениях плоскопараллельного двухслойного течения вязкой теплопроводной жидкости // ПММ. (В печати). - Ефимова М. В.
Термокапиллярная конвекция двухслойной системы жидкостей со свободной границей // Сб. докл. всерос. науч. конф. «Фундаментальные и прикладные вопросы механики и процессов управления» (электронный ресурс). Владивосток: ИАПУ ДВО РАН. — 2011. — С. 236–239 .
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ №
Руководитель: член-корреспондент РАН В. В. Шайдуров
1. Работа направлена на численное решение системы уравнений Навье-Стокса для вязкого сжимаемого теплопроводного газа. Для этого привлекается комбинация методов траекторий и конечных элементов. Метод траекторий заключается в аппроксимации суммы первых производных каждого уравнения системы (субстанциональных производных) назад по времени вдоль траекторий движения частиц. Метод траекторий впервые появился в работах французских и американских ученых для аппроксимации уравнений Навье-Стокса для вязкой несжимаемой жидкости с первым порядком аппроксимации и для одного уравнения переноса массы. В наших исследованиях он применяется к полной системе уравнений Навье-Стокса. Совокупность метода траекторий и метода конечных элементов не требует согласования триангуляций на соседних временных слоях, что значительно облегчает динамическое разрежение или сгущение триангуляций по времени для оптимизации вычислительной работы или улучшения аппроксимации в пограничных слоях и ударных волнах. Для решения систем алгебраических уравнений используется многосеточный метод с внешними итерациями по нелинейности.
На первом этапе была реализована одномерная задача о распространении теплового импульса большой мощности в вязком теплопроводном газе. Проведены вычислительные эксперименты на высокопроизводительной вычислительной технике для различных чисел Маха и Рейнольдса. Тестовые расчёты продемонстрировали более высокую точность решения при одинаковых вычислительных затратах, чем используемые исследовательские и индустриальные пакеты прикладных программ решения этих уравнений в полной постановке для высоких скоростей.
2. Продолжались работы по эффективному распараллеливанию метода конечных элементов (МКЭ) на неструктурированных сетках для эллиптических систем уравнений на различных архитектурах высокопроизводительных вычислительных систем (ВС).
Для ВС с общей памятью была реализована, отлажена и исследована на эффективность параллельная версия разработанного в коллективе ПО.
Для описания эффективности распараллеливания принято использовать параметр $\textit{Sp}$ — ускорение параллельного алгоритма на $\textit{p}$ процессах (нитях) $\textit{S${}_{p}$ = T${}_{1 }$/ T${}_{p}$}$, где $\textit{T${}_{1}$}$ — время выполнения последовательного кода, $\textit{T${}_{p}$ }$ — время выполнения параллельной программы на $\textit{p}$ процессах (нитях).
Показано, что подключение библиотеки OpenMP в нашем случае дает большие затраты времени на синхронизацию нитей за счет наличия зависимости по данным в теле основного цикла (табл. VI.2). Это приводит к падению эффективности многопоточной программы при сравнеии ее с самым эффективным последовательным кодом, а также к возможности неоднозначного вычисления ускорения $\textit{S${}_{p}$}$ из-за сильной вариативности числителя $\textit{T${}_{1}$}$. Если считать ускорение параллельной программы по отношению к последовательному коду с подключенной библиотекой, то оно окажется значительно лучше ускорения по отношению к самому эффективному последовательному коду. Везде, где отмеченная разница существенна при вычислении ускорения в качестве $\textit{T${}_{1}$}$ бралось время выполнения самой эффективной версии последовательной программы на одном узле соответствующего кластера.

Таблица VI.2. Время выполнения основного цикла последовательной программы
Для основных циклов программы исследовано время их выполнения в зависимости от выбора стратегии распределения итераций цикла по нитям (рис. VI. 7). Расчеты показали, что затраты на синхронизацию нитей при различных подходах к декомпозиции тела цикла по нитям во всех исследованных случаях (static, dynamic, guaided) отличается незначительно, однако стратегия static дает наиболее устойчивые результаты, поэтому была принята за основу.
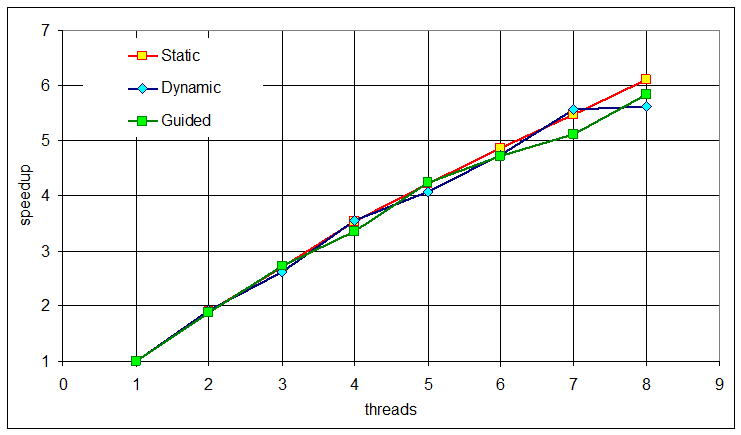
Рис. VI.7. Зависимость ускорения от количества нитей для различных стратегий распределения нитей внутри цикла
Ускорение основных циклов OpenMP-версии программы в зависимости от количества нитей по сравнению со временем выполнения этой же OpenMP-версии на одной нити для одного узла нескольких SMP-узловых кластерных ВС показано на рис. VI.8. Компиляция кода во всех случаях проводилась компилятором Intel без дополнительной оптимизации. Вычислительный эксперимент (рис. VI.8) показал, что на различных кластерных системах ускорение варьируется довольно сильно, от оптимистичной оценки для кластера СФУ до весьма неблагоприятной для кластерных систем ТГУ и ИВМ СО РАН. В настоящее время не удалось определить фактор, влияющий на ухудшение масштабируемости алгоритма для последних двух кластерных систем, и требуются дальнейшие исследования в этом направлнении.
Для SMP-узловых кластерных ВС была реализована, отлажена и исследована на эффективность параллельная версиия разработанного в коллективе ПО, реализующего МКЭ на неструктурированной согласованной триангуляции с использованием технологии OpenMP для распараллеливания внутри SMP-узла и технологии MPI — между узлами кластера. Из графиков ускорений относительно наиболее эффективной последовательной программы (рис. VI.9) видно, что технология MPI, примененная для распараллеливания как между узлами кластера, так и внутри одного узла дает большую эффективность по сравнению с совмещенной MPI+OpenMP-технологией. По всей вероятности, это связано с тем, что основные циклы программы содержат зависимости по данным, что увеличивает время синхронизации на общей памяти.
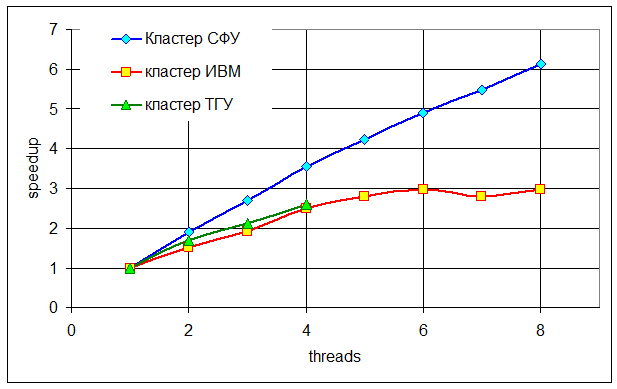
Рис. VI.8. Зависимость ускорения основного цикла OpenMP-версии программы от количества нитей, полученного на одном узле нескольких SMP-узловых кластерных ВС
Для повышения эффективности распараллеливания на общей памяти предложено изменить алгоритм сборки невязки по локальным матрицам жесткости с поэлементного на поузловой, что приведет к уменьшению зависимости по данным в основных циклах, но в тоже время усложнит структуры хранения триангуляции.
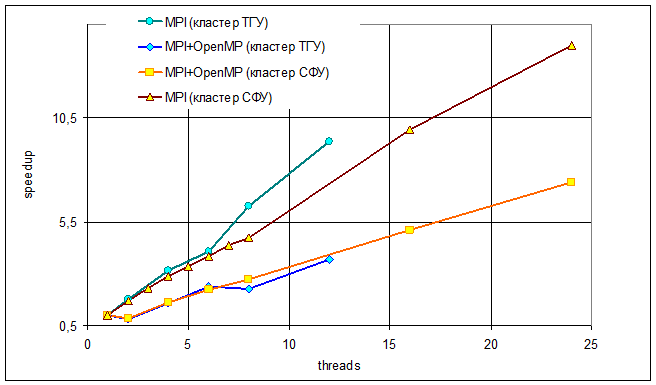
Рис. VI.9. Зависимость ускорения основного цикла параллельной программы от количества нитей, полученного с помощью технологии MPI и совмещения технологий OpenMP и MPI на SMP-узловых кластерных ВС СФУ и ТГУ
В отчетный период начаты также работы по написанию эффективной программы, реализующей МКЭ c использованием технологии CUDA. В настоящее время разработаны алгоритмы для равномерной триангуляции, дающие ускорение до 8 раз. Исследования в данном направлении будут продолжены.
Основные публикации:
- Шайдуров В. В., Щепановская Г. И., Якубович М. В.
Применение метода траекторий и метода конечных элементов в моделировании движения вязкого теплопроводного газа // Вычислительные методы и программирование. — 2011. — Т. 12. — С. 275–281 . - Зализняк В. Е., Щепановская Г. И.
Теория и практика по вычислительной математике. — Красноярск: СФУ. — 2011. — 120 с. - Якубович М. В.
Численное моделирование плоского течения вязкого теплопроводного газа в канале // Программа и тез. докл. XII Всерос. конф. молодых ученых по математическому моделированию и информационным технологиям.? Новосибирск. — 2011. — С. 26. - Karepova E. D., Shaidurov V. V.
A parallel implementation of FEM for a boundary value problem for the shallow water equations // Notes on Numerical Fluid Mechanics and Multidisciplinary Design. — 2011. — V. 115. — P. 29-42. - Karepova E., Shaidurov V., Dementyeva E.
The numerical solution of data assimilation problem for shallow water equations // Int. J. of Num. Analysis and Modeling, Series B. — 2011. — V. 2 (2-3). — P. 167–182 . - Karepova E., Dementyeva E.
Solution of Assimilation Observation Data Problem for Shallow Water Equations for SMP-Nodes Cluster // Lecture Notes in Computer Science. — 2011. — V. 6873. — P. 444–451 . - Дементьева Е. В., Карепова Е. Д., Малышев А. В.
Эффективность численного моделирования на кластерных системах распространения поверхностных волн // Вестник НГУ, Серия: информационные технологии. — 2011. — Т. 9. — Вып. 1. — С. 11-20.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель: член-корр. РАН А. Г. Дегерменджи, ответственный исполнитель от ИВМ д.ф.-м.н. В. М. Белолипецкий
Предложен метод для определения потока СО${}_{2}$ ($Q_{C} $), использующий точечную модель для концентраций углекислого газа в атмосфере и измеренные на высоких вышках профили концентраций в атмосфере. Показано, что для оценки потока $Q_{C} $ достаточны данные измерений концентраций СО${}_{2 }$ на уровне вышки. Выполнен анализ данных измерений концентраций СО${}_{2}$ на вышке, взятых с сервера ftp://ftp.cmdl.noaa.gov/ccg/towers/.
Среднемесячные концентрации СО${}_{2}$, измеренные в хорошо перемешанной области атмосферного пограничного слоя (АПС) с 400 метровой вышки, отражают постоянно присутствующую разницу в несколько ppm между концентрацией СО${}_{2}$ в АПС и в свободной тропосфере (СТ) [Helliker, B., Berry, J., Betts, A., Davis, K., Bakwin, P., 2004, Estimates of ABL-scale net carbon dioxide flux in Central Wisconsin. Transitions of American Geophysical placeUnion. 84(46)]. Концентрации, измеряемые на высокой вышке, являются результатом процессов на области порядка 10${}^{4}$ км${}^{2}$ [Cleugh, H.A., Grimmond, C.S.B. 2001, Modelling regional scale surface energy exchanges and CBL growth in a heterogeneous, urban-rural landscape. Boundary layer meteorology. 98, pp. 1-31].
Метод баланса АПС фокусируется на процессах, которые влияют на баланс CO${}_{2}$ в континентальной атмосфере на месячном и сезонном временных масштабах. Значительные (в несколько ppm) и постоянные горизонтальные градиенты концентрации формируются на масштабах в сотни км, а различие в несколько ppm между пограничным слоем высотой 1-2 км и тропосферой над ним присутствует почти постоянно. Поэтому, хотя горизонтальный перенос может вызывать большие изменения концентрации CO${}_{2}$ в отдельные дни, среднемесячные концентрации определяются вертикальным обменом.
Из уравнения баланса СО${}_{2}$ в АПС, проинтегрированного от поверхности до максимальной дневной высоты АПС $H_{K} $ в предположении, что горизонтальный перенос может не учитываться, получается соотношение для определения потока с поверхности $Q_{C} $
\[Q_{C} =H_{K} \frac{d{\kern 1pt} \varphi }{d{\kern 1pt} t} +W(C-C_{FT} ),\]
где $\textit{C}$ — молярная концентрация CO${}_{2}$ (мкмоль CO${}_{2}$ на моль сухого воздуха, ppm), $C_{FT} $ — концентрация СО${}_{2}$ в СТ, $\varphi =\frac{1}{H_{K} } \int _{0}^{HK}C{\kern 1pt} d{\kern 1pt} z $, $W$ — величина (по модулю) вертикальной скорости (по модулю) на высоте $H_{K} $.
Эта формула использовалась для вычисления $Q_{C} $ по измерениям на Зотинской вышке. Среднесуточные концентрации CO${}_{2}$, измеренные на 300 м, рассматривались как средние концентрации в АПС. Регулярные измерения концентрации CO${}_{2}$ в СТ проводились в районе Зотино в 19
Основные публикации:
- Белолипецкий В. М., Белолипецкий П. В.
Оценка потока углерода между атмосферой и наземной экосистемой по измеренным на вышке вертикальным распределениям СО2 // Вестник НГУ. — 2011. — Т. 9. — Вып. 1. — С. 75-81.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., проф. А. Н. Горбань
Семинару были представлены 37 докладов от 62 участников из различных регионов Российской Федерации и СНГ.
Цель семинара — объединение усилий специалистов различных областей науки. Общение на семинаре позволяет взглянуть на конкретную проблему с точки зрения различных областей науки и найти новые, нетрадиционные подходы к ее решению.
Основные материалы семинара, в соответствии с его научной программой могут быть разделены на три раздела:
- применение нейронных сетей в биологии и генетике;
- применение нейронных сетей в медицине;
- развитие и приложение теории нейроинформатики: применение принципов нейроинформатики в экспериментальной физике, социальных науках; организации работы городского транспорта, морского судовождения и др.
В решении семинара, принятом в ходе заключительной дискуссии, констатируется все большее расширение аппарата нейроинформатики и расширение области ее применения. Одновременно отмечается тенденция к дальнейшему размыванию границ нейроинформатики и все большей интеграции нейронных сетей в другие области. Отмечен также рост числа докладов, связанных с нейроинформатикой в «широком» смысле и увеличение числа докладов, относящихся к обработке данных.
Основные публикации:
- «Нейроинформатика, её приложения и анализ данных». Материалы XIX Всероссийского семинара / Под ред. А. Н. Горбаня, Е. М. Миркеса
. — ИВМ СО РАН — Красноярск. — 2011. — 190 с. — ISBN 978-5-7638–240 2-5.
(Отдел моделирования неравновесных систем)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., проф. В. В. Слабко (СФУ)
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. А. Н. Горбань
Ежегодный Всероссийский семинар «Моделирование неравновесных систем» МНС-2011 проводился при поддержке РФФИ с 7 по 9 октября 2011 г. на базе Института вычислительного моделирования (ИВМ СО РАН), Красноярск, Академгородок.
На семинаре были представлены 66 докладов от 93 авторов из различных регионов Российской Федерации и СНГ, а также Института Кюри, Франции. Материалы семинара опубликованы к началу его работы.
Основные материалы семинара, в соответствии с его научной программой, могут быть разделены на три раздела:
- разработка математического и программного обеспечения моделирования нелинейных, нестационарных и неоднородных по пространству процессов;
- развитие методов имитационного моделирования сложных систем в физике, химии, технике, биологии, медицине, экономике и финансах;
- приложение методов моделирования к решению физических, биологических и медицинских задач и других проблем.
Подобная классификация материалов достаточно условна, однако она соответствует основным направлениям исследований в области моделирования неравновесных систем, и позволяет проанализировать представленные доклады либо на методологической основе, либо на основе общности объектов исследований.
Принято решение о продолжении ежегодного проведения семинаров с обязательным привлечением большего числа студентов и молодежи.
Основные публикации:
- «Моделирование неравновесных систем — 2011». Материалы XIV Всероссийского семинара / Под ред. А. Н. Горбаня, Е. М. Миркеса
. — ИВМ СО РАН — Красноярск — 2011 — 217 с.
(Отдел моделирования неравновесных систем)
| К началу | |
Грант РФФИ №
Руководитель: к.ф.-м.н. М. П. Варыгина
| К началу | |
Грант РФФИ №
Руководитель: Е. В. Дементьева
| К началу | |
Грант РФФИ
Руководитель: к.т.н. А. А. Кадочников
Международная конференция Математические и информационные технологии MIT-2011 (IX конференция «Вычислительные и информационные технологии в науке, технике и образовании») проходила с 27.08.2011 по 31.08.2011 в г. Врнячка Баня, Сербия и с 31.08.11 по 05.08.11 в г. Будва, Черногория. Научная программа конференции включала в себя следующие направления:
- вычислительные технологии (численное моделирование сложных физических явлений: методы, алгоритмы, программы, результаты; теория и практика высокопроизводительных вычислений);
- информационные и телекоммуникационные технологии (модели, методы и технологии обработки пространственных данных; интеграция распределенных информационных ресурсов; новые телекоммуникационные технологии);
- математические технологии (дифференциальные уравнения в задачах естествознания и техники; уравнения в частных производных — теория и приложения; комплексный анализ; фундаментальные и прикладные задачи математической статистики и теории вероятностей).
В конференции приняли участие более 140 специалистов из научных центров, исследовательских институтов, университетов, представляющих Боснию и Герцоговину, Германию, Казахстан, Ливию, Македонию, Россию, Сербию, Францию и Черногорию.
Средства финансирования, выделенные РФФИ, были использованы для оплаты транспортных расходов, проживания и оплаты оргвзноса.
Участвуя в работе конференции М. П. Варыгина выступила с устным сообщением на тему «Параллельные вычисления в задачах динамики сред с микроструктурой».
Участвуя в работе конференции Е. В. Дементьева была содокладчиком устного сообщения на тему «Численное решение задачи на ассимиляцию данных наблюдений для уравнений мелкой воды» и выступила со стендовым докладом «Численное моделирование распространения длинных волн в больших акваториях с помощью SMP-узловых кластеров».
Участвуя в работе конференции А. А. Кадочников, выступил со стендовым докладом «Разработка картографических сервисов для информационно-аналитических систем в региональном управлении».
Основные публикации:
- Варыгина М. П.
Параллельные вычисления в задачах динамики сред с микроструктурой // Математические и информационные технологии, MIT-2011 [Электронный ресурс] / Международная конференция (IX конференция «Вычислительные и информационные технологии в науке, технике и образовании), Врнячка Баня, Сербия, 27-31 августа 2011 г., Будва, Черногория, 31 августа — 5 сентября 2011 г., № гос. регистрации — 0321102644, Режим доступа: http://conf.nsc.ru/files/conferences/MIT-2011/fulltext/49098/56726/varyginaMIT.pdf, свободный. — Загл. с экрана (дата обращения: 15.11.2011). - Дементьева Е. В., Карепова Е. Д., Малышев А. В.
Численное моделирование распространения длинных волн в больших акваториях с помощью SMP-узловых кластеров // Математические и информационные технологии, MIT-2011 [Электронный ресурс] / Международная конференция (IX конференция «Вычислительные и информационные технологии в науке, технике и образовании), Врнячка Баня, Сербия, 27-31 августа 2011 г., Будва, Черногория, 31 августа — 5 сентября 2011 г., № гос. регистрации — 0321102644, Режим доступа: http://conf.nsc.ru/files/conferences/MIT-2011/fulltext/42116/56787/Dementyeva.pdf, свободный. — Загл. с экрана (дата обращения: 15.11.2011). - Кадочников А. А.
Разработка картографических сервисов для информационно-аналитических систем в региональном управлении // Математические и информационные технологии, MIT-2011 [Электронный ресурс] / Международная конференция (IX конференция «Вычислительные и информационные технологии в науке, технике и образовании»), Врнячка Баня, Сербия, 27-31 августа 2011 г., Будва, Черногория, 31 августа — 5 сентября 2011 г., № гос. регистрации — 0321102644, Режим доступа: http://conf.nsc.ru/files/conferences/MIT-2011/fulltext/50479/56591/KadochnikovAA.pdf, свободный. — Загл. с экрана (дата обращения: 23.12.2011).
(Отделы Вычислительной математики, Вычислительной механики деформируемых сред, Вычислительной физики)
| К началу | |
Грант РФФИ №
Руководитель: к.ф.-м.н. И. И. Рыжков
Международная конференция Европейской ассоциации исследований при пониженной гравитации проходила 6-9 сентября 2011 года в г. Антверпен (Бельгия).
Симпозиум проводится ассоциацией ELGRA каждые два года и посвящен обсуждению результатов исследований в условиях микрогравитации в различных областях знаний. Сюда относятся материаловедение, физика жидкостей, биология, физиология человека, животных и растений, биотехнология. Количество участников конференции — около 200.
Сделан доклад «О термокапиллярной неустойчивости в жидких мостах».
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ
Руководитель: к.т.н. Т. Г. Пенькова
Международная конференция «Технологии разработки информационных систем» (ТРИС-2011) проходила с 18 по 24 сентября 2011 г. в городе Геленджике. В рамках работы конференции обсуждались актуальные проблемы и решения в области анализа и синтеза информационных систем и процессов, инженерии знаний, развития и применения современных технологий и методов в различных прикладных областях.
Пенькова Т. Г. выступила с докладами: «Формирование управляющих рекомендаций на основе результатов оценивания благополучия территории»; «Поддержка построения оперативных аналитических запросов на основе интегральной OLAP-модели». Представленные работы опубликованы в сборнике материалов конференции ТРИС-2011. По итогам конференции опубликована статья Т. Г. Пенькова, А. В. Коробко «Построение интегральной OLAP-модели на основе формального концептуального анализа» в спецвыпуске журнала «Информатизация и связь», входящем в перечень изданий ВАК.
Грант использован на компенсацию расходов на командировку (транспортные расходы и проживание), связанных с участием в работе конференции.
Основные публикации:
- Пенькова Т. Г., Коробко А. В.
Построение интегральной OLAP-модели на основе формального концептуального анализа // Информатизация и связь. — 2011. — № 3. — С. 23-25. - Пенькова Т. Г., Коробко А. В.
Поддержка построения оперативных аналитических запросов на основе интегральной OLAP-модели // Материалы междунар. науч.-технич. конф. «Технологии разработки информационных систем». — Таганрог: Технологический ун-т ЮФУ. — 2011. — Т. 1. — P. 68-71. - Пенькова Т. Г.
Формирование управляющих рекомендаций на основе результатов оценивания благополучия территории // Сб. материалов междунар. науч.-технич. конф. «Технологии разработки информационных систем». — Таганрог: Технологический ун-т ЮФУ. — 2011. — Т. 1. — P. 62-65.
(Отдел прикладной информатики)
| К началу | |