| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2012 год
Программы фундаментальных исследований Президиума РАН
Программа № 15 «Информационные, управляющие и интеллектуальные технологии и системы»
Координаторы программы: академик РАН С. В. Емельянов, академик РАН Ю. И. Журавлев
Проект 15.3. Разработка интеллектуальных вычислительных комплексов для поддержки принятия решений при конструировании и эксплуатации сложных технических систем и объектовРуководители: академик РАН Ю. И. Шокин, д.т.н., профессор Л. Ф. Ноженкова
Предложен метод концептуального OLAP-моделирования, основанный на интеграции технологии OLAP и метода анализа формальных понятий. Метод заключается в применении анализа формальных понятий к объектам оперативного анализа данных (показателям и измерениям) с использованием экспертных знаний о возможности их совместной аналитической обработки. Разработаны алгоритмы формирования концептуальной OLAP-модели предметной области. Алгоритм поиска кубов-концептов основан на итеративной реализации метода Крайеса. Алгоритм построения концептуальной решетки OLAP-кубов представляет собой адаптацию алгоритма формирования концептуальной решетки NEIGHBORS. Такие свойства концептуальной OLAP-модели, как полнота OLAP-кубов и отношение частичного порядка между ними, позволяют говорить о возможности применения предложенного подхода для адаптивного манипулирования объектами модели и формирования OLAP-куба произвольной аналитической задачи.
Разработаны аналитические средства оценки последствий аварийных ситуаций на опасных промышленных объектах на основании данных оперативного мониторинга метеорологической обстановки, показаний сенсоров опасных химических веществ, радиометров и моделирования распространения поражающих факторов техногенных чрезвычайных ситуаций.
Ведутся работы по разработке системы мониторинга и поддержки планирования, размещения и контроля процедур муниципального заказа — АИС «Муниципальный заказчик». Определены базовые функциональные блоки системы. Выполнено развитие средств ведения справочников — добавлены функции работы с журналами данных на основе SQL-представлений. Созданы оригинальные средства синхронизации баз данных, основанные на использовании промежуточного веб-сервера в качестве сервера обмена данными.
Основные публикации:
- Ничепорчук В. В., Ноженкова Л. Ф.
Экспертная ГИС поддержки принятия решений в паводкоопасных ситуациях для территорий Сибирского региона // Вестник КемГУ, 2012. — № 3/1 (51). — С. 91-97. - Penkova T., Nicheporchuk V., Korobko A.
Emergency situations monitoring using OLAP technology // Proc. of the 35-th Int. Convention. The Conf. «Business Intelligence Systems (miproBIS)». — Croatia, Opatija, 2012. — P. 1941–194 6. - Пенькова Т. Г., Коробко А. В.
Аналитическая поддержка принятия решений на основе концептуальной OLAP-модели предметной области // Материалы XI Всерос. науч.-техн. конф. «Теоретические и прикладные вопросы современных информационных технологий» (ТиПВСИТ'2012), Улан-Удэ, 2012. — С.393–399 .
(Отдел прикладной информатики)
| К началу | |
Программа № 18 «Алгоритмы и математическое обеспечение для вычислительных систем сверхвысокой производительности»
Координаторы программы: академик РАН В. Б. Бетелин, член-корреспондент РАН Б. Н. Четверушкин
Проект 18.2. Решение задач газовой и гидродинамики на высокопроизводительных вычислительных системах№ гос. регистрации 01201268796
Руководители: член-корреспондент РАН В. В. Шайдуров, д.ф.-м.н., профессор В. М. Садовский
Блок 1. Вычислительные алгоритмы для решения уравнений Навье-Стокса вязкого теплопроводного газа (В. В. Шайдуров, Г. И. Щепановская, Л. В. Гилева, А. В. Вяткин, М. В. Якубович).
Созданы и реализованы вычислительные алгоритмы для решения двумерных нестационарных уравнений Навье-Стокса вязкого теплопроводного газа на высокопроизводительных вычислительных комплексах. Аппроксимация по времени состоит в применении новой модификации метода конечных объемов для инерциальных производных вдоль траекторий движения частиц газа, что обеспечивает выполнение законов сохранения и устойчивость на дискретном уровне. Получающаяся последовательность стационарных задач на каждом шаге по времени решается методом конечных элементов. В предложенном подходе используются прямоугольные кусочно-равномерные триангуляции везде, кроме тонкой полосы вблизи поверхности тела, где элементы точно согласованы с этой поверхностью. Такой тип триангуляции позволяет применить бикубические эрмитовы конечные элементы, обеспечивающие гладкость решения по пространству из класса С(1) и возможность прямого вычисления невязки приближенного решения. Вблизи границы эти элементы дополняются новым классом кубических элементов, поддерживающим указанную гладкость решения во всей области определения. В целом по вычислительной области эта совокупность конечных элементов обеспечивает четвертый порядок аппроксимации по пространству.
Вычислительные алгоритмы реализованы для решения задачи течения газа в канале с уступом. Проведены вычислительные эксперименты, подтвердившие теоретические выводы и оценки. Полученная схема численного решения действительно пригодна для широкой области чисел Маха и Рейнольдса без традиционных ограничений на шаг сетки по времени, а получаемые вычислительные результаты хорошо соответствуют экспериментальным представлениям.
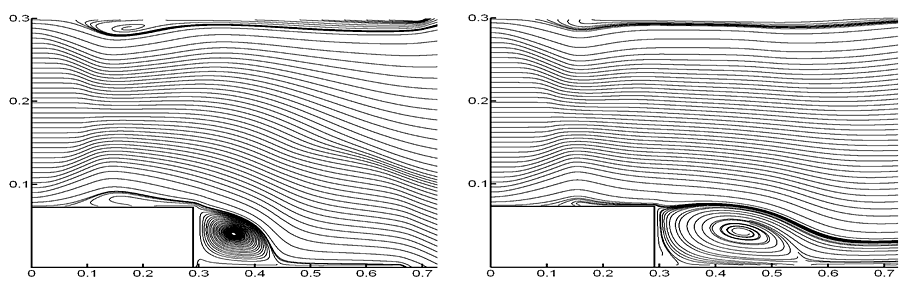
Рис. IV.1. Траектории частиц газа для параметров M = 2, Re = 2000 в моменты времени t = 0.9 (слева) и t = 1.5 (справа)
Численная реализация построенных алгоритмов осуществлена для высокопроизводительных вычислительных кластеров. На рис. приведены траектории частиц газа в сверхзвуковом течении вязкого теплопроводного газа в плоском канале с прямоугольным уступом для различных моментов времени.
Блок 2. Разработка программного обеспечения для численного исследования процессов распространения волн напряжений и деформаций в структурно неоднородных блочных средах типа горных пород с учетом нелинейных эффектов взаимодействия блоков через тонкие прослойки (В. М. Садовский, О. В. Садовская, М. П. Варыгина).
Разработаны вычислительные алгоритмы, моделирующие динамическое взаимодействие упругих блоков через тонкие упругие и вязкоупругие прослойки при плоской деформации. Численное решение задачи строилось на основе схемы распада разрыва Годунова на равномерной сетке с выбором предельно допустимого по условию Куранта-Фридрихса-Леви шага по времени. При меньших значениях шага использовалась кусочно-линейная ENO-реконструкция второго порядка точности. Для решения двумерных задач применялся метод двуциклического расщепления, приводящий к решению одномерных задач. Выполнено распараллеливание алгоритмов для вычислительных систем на графических ускорителях по технологии CUDA для различных типов прослоек: упругая модель, вязкоупругие модели Максвелла и Кельвина-Фойхта. Решались задачи о распространении плоских продольных волн, вызванных кратковременными и длительными импульсными воздействиями на границе слоистой (блочной) среды. В двумерной постановке численно решалась задача Лэмба о действии мгновенной сосредоточенной нагрузки на поверхности полупространства (рис. IV.2). Исследование эффективности параллельной реализации алгоритма показало ускорение работы программы до 50 раз по сравнению с однопроцессорной версией.
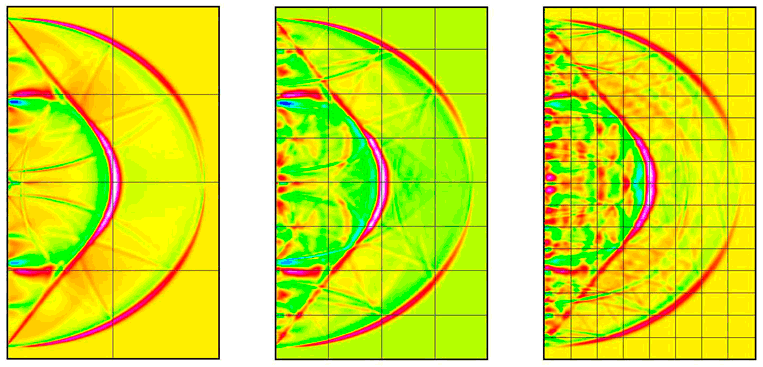
Рис. IV.2. Волновая картина распределения касательного напряжения в задаче Лэмба о сосредоточенном импульсном воздействии на границе блочной среды (слева направо — 8, 32 и 128 блоков)
На основе метода конструирования разностных схем с контролируемой диссипацией энергии, предложенного Ивановым при решении задач динамики упругой среды, построена экономичная безусловно устойчивая схема типа предиктор-корректор для решения параболических систем уравнений динамической теории вязкоупругости Кельвина-Фойхта и динамической теории вязкопластичности, имеющая определенные алгоритмические преимущества перед известными схемами. Выполнена ее программная реализация на компьютере с последовательными вычислениями и проведены тестовые расчеты.
В среде MATLAB для вычислительных систем с графическими ускорителями разработана компьютерная программа, реализующая метод характеристик для численного решения задачи Коши для гиперболической системы уравнений первого порядка общего вида относительно двух независимых переменных. На основе этой программы проведены методические расчеты плоской задачи теории идеальной пластичности (задачи Генки), задачи статики сыпучей среды (задачи Соколовского) и осесимметричной задачи полной пластичности (задачи Ишлинского).
Блок 3. Оценка потенциального параллелизма при численном решении краевых задач для эллиптических уравнений на SMP-узловых кластерах (Е. Д. Карепова, Е. В. Дементьева, магистранты ИМ СФУ: Д. А. Демидов, А. А. Ефремов).
Для задачи Дирихле для уравнения в частных производных второго порядка эллиптического типа в многоугольной области построен метод конечных элементов (МКЭ) с линейными треугольными конечными элементами на неструктурированной согласованной триангуляции. В задачу этапа 2012 г. входила оценка потенциального параллелизма при реализации подобного класса задач на SMP-узловых кластерах.
Для оценки эффективности разработанных параллельных программ используются два показателя: ускорение, получаемое параллельной программой при выполнении ее на $\textit{р}$ процессорах (ядрах) ($S_{p} (N)=T_{1} (N)/T_{p} (N)$) и эффективность параллельной программы ($E_{p} (N)=S_{p} (N)/p$). Здесь $T_{1} $ — время, затраченное на выполнение последовательной программы, $T_{p} $ — время, затраченное на выполнение параллельной программы на $\textit{p}$ процессорах (ядрах), $\textit{N}$ — характеризует вычислительную сложность задачи.
Ясно, что рост производительности параллельной программы при росте числа процессов должен быть достаточен, чтобы имело смысл использовать суперкомпьютер.
Заметим, что время выполнения программы на одном процессе $T_{1}$ в общем случае состоит из времени, которое затрачивается собственно на вычисления и времени обращения к памяти: $T_{1} (N)=T_{1}^{calc} (N)+T_{1}^{mem} (N)$. Следует отметить также, что современные компиляторы имеют широкие возможности оптимизации кода. Например, при подключении оптимизации -O2 при компиляции Intel C compiler Version 11.1 время выполнения последовательной программы уменьшается более чем в два раза в сравнении с опцией -O0. Возможности оптимизации резко падают при подключении библиотек MPI или OpenMP.
Время выполнения MPI-программы на $\textit{p}$ MPI-процессах (по одному MPI-процессу на ядро) состоит из времени, затрачиваемого на выполнение вычислений, времени работы с памятью и времени, затрачиваемого на обмены: $T_{p} (N)=T_{p}^{calc} (N)+T_{p}^{mem} (N)+T_{p}^{comm} ({p})$. Причем время, затраченное на вычисления и работу с памятью, как правило, уменьшается пропорционально задействованному количеству MPI-процессов, поскольку эти операции происходят параллельно. Время обменов, следует отнести к накладным расходам:
\[T_{p} (N)\approx \frac{T_{p}^{calc} (N)+T_{p}^{mem} (N)}{p} +T_{p}^{comm} (p).\]
Время выполнения OpenMP-программы на $\textit{Th}$ OpenMP-нитях состоит из времени, затрачиваемого на выполнение вычислений, времени работы с памятью и времени, затрачиваемого на создание, уничтожение и синхронизацию нитей: $T_{Th} (N)=T_{Th}^{calc} (N)+T_{Th}^{mem} (N)+T_{Th}^{synch} (Th).$ Причем время, затраченное на вычисления, как правило, уменьшается пропорционально задействованному количеству OpenMP-нитей, поскольку вычисления происходят параллельно. Время параллельной работы $\textit{Th}$ нитей с общей памятью также уменьшается, но одновременное чтение и запись несколько ухудшают степень параллелизма работы с памятью. Время создания, уничтожения и синхронизации нитей следует отнести к накладным расходам:
\[T_{Th} (N)=\frac{T_{1}^{calc} (N)+\gamma T_{1}^{mem} (N)}{Th} +T_{Th}^{synch} (Th), ~~~ 0 \lt \gamma \lt 1.\]
Таким образом, для получения хорошего ускорения MPI-программы необходимо, чтобы время, затрачиваемое на обмены, было значительно меньше времени, затрачиваемого на вычисления и работу с памятью. Для получения хорошего ускорения OpenMP-программы необходимо, чтобы накладные расходы многопоточности были невелики по сравнению с вычислениями.
Сборка невязки при реализации метода конечных элементов на согласованной неструктурированной триангуляции для рассматриваемого класса задач может производиться по элементам (традиционный способ, реализующий наиболее выгодное распределение памяти) или по узлам сетки (приводит к необходимости создания в памяти структур переменного размера). При последовательной реализации алгоритма наиболее эффективным считается поэлементная сборка.
В рассматриваемом классе задач при распараллеливании для системы с распределенной памятью используется подход, связанный с декомпозицией вычислительной области без теневых граней, использующийся для сборки невязки в каждой точке вычислительной сетки при решении системы линейных алгебраических уравнений итерационными методами. С декомпозицией связаны следующие неизбежные накладные расходы: 1) время, затрачиваемое на обмены точка-точка на каждом шаге итерации для сборки невязки на границах разреза вычислительной области; 2) дополнительные операции, связанные с перераспределением (буферизацией) данных на разрезах при обменах; 3) время на коллективную операцию глобальной редукции для расчета критерия останова итерационного процесса. Следует отметить, что время, затрачиваемое на п. 1-2 при использовании неблокирующих обменов не зависит от количества MPI-процессов, а время в п. 1 дает логарифмический рост при увеличении числа MPI-процессов.
При распараллеливании для системы с общей памятью для рассматриваемого класса задач характерны следующие накладные расходы: 1) время на создание и уничтожение нитей; 2) время на распределения итераций основных циклов по нитям (возможно использование, по крайней мере, трех механизмов); 3) синхронизация нитей внутри тела основного цикла при сборке невязки по элементам; 4) время на операцию глобальной редукции для расчета критерия останова итерационного процесса. Показано, что для систем с общей памятью алгоритм сборки невязки в МКЭ существенно влияет на эффективность параллельной реализации. В частности, на синхронизацию нитей внутри основного цикла при поэлементной сборке тратится до 40% времени. Таким образом, для параллельных программ на общей памяти эффективнее использовать поузловую сборку невязки, при которой накладные расходы на синхронизацию нитей п. 3 совсем не нужны. Однако появляются дополнительные расходы, связанные с неравномерным распределением данных в памяти.
Кроме того, очевидно, что выгода от совместного использования технологий OpenMP и MPI по сравнению с MPI может быть получена только, если накладные расходы на поддержку нитей будут меньше накладных расходов на обмен сообщениями. Так при использовании $\textit{p}$ MPI-процессов по $\textit{Th }$нитей в каждом (по одной нити на ядро) реализация OpenMP+MPI будет иметь преимущество над чистой MPI-реализацией (по одному MPI-процессу на ядро), если выполнится следующее соотношение:
\[\frac{\gamma }{Th} T_{1}^{mem} (N)+T_{Th}^{synch} (Th)+T_{p}^{comm} (p)\ll T_{p\times Th}^{comm} (p\times Th).\]
Ниже (рис. IV.3−IV.5) приведены результаты численных экспериментов для последовательной и нескольких параллельных реализаций решения задачи о распространении поверхностных волн в большой открытой акватории с помощью метода конечных элементов на согласованной неструктурированной триангуляции.
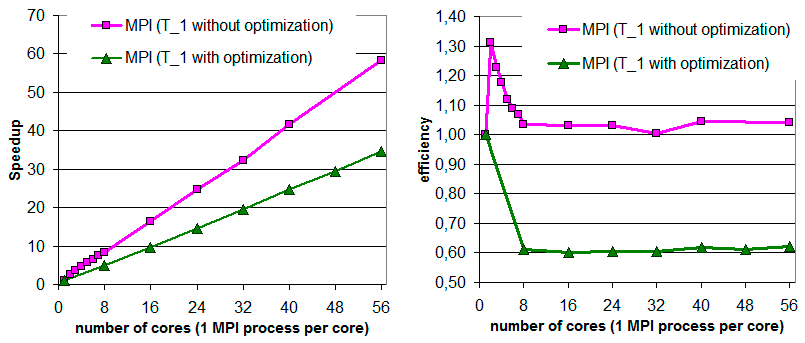
Рис. IV.3. Ускорение (слева) и эффективность (справа) MPI-программы. Характеристики вычислены относительно времени последовательной программы, откомпилированной без оптимизации (розовые кривые) и с включенной оптимизацией -O2 (зеленые кривые)
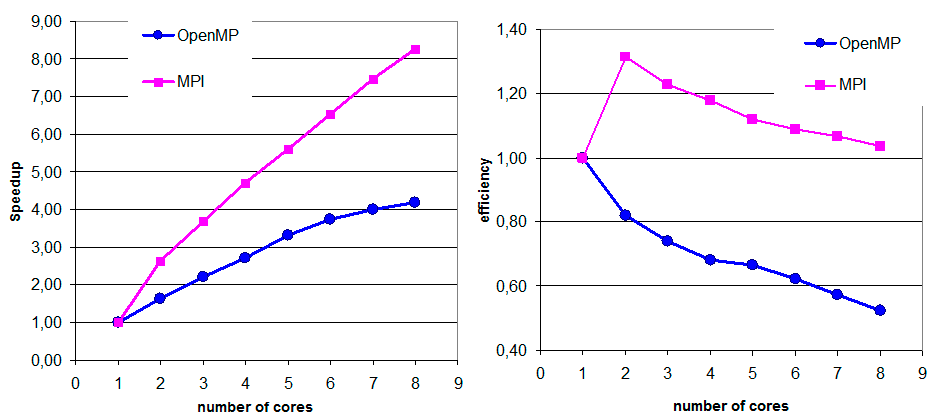
Рис. IV.4. Ускорение (слева) и эффективность (справа) OpenMP-программы (одна нить на ядро) и MPI-программы (один MPI-процесс на ядро)
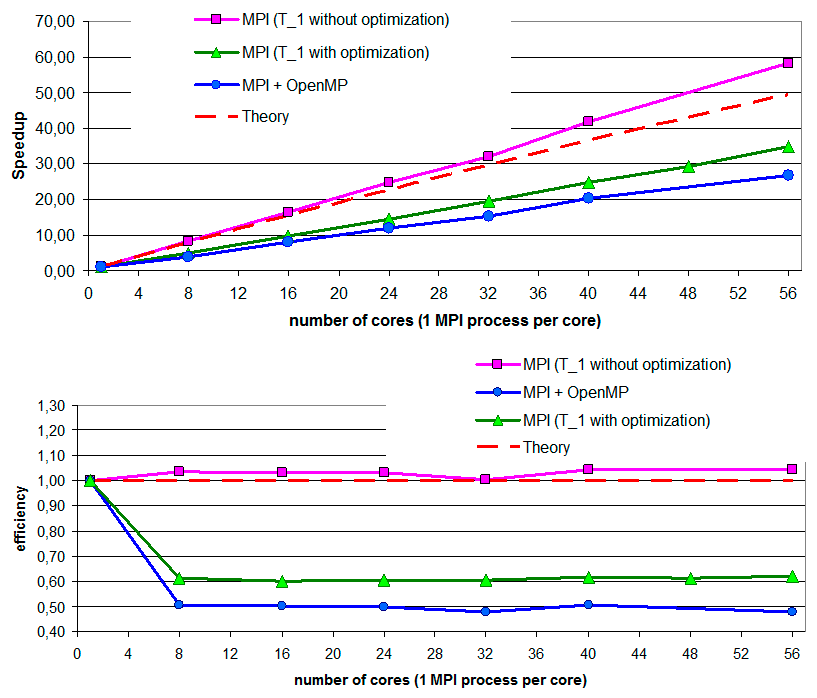
Рис. IV.5. Ускорение (сверху) и эффективность (снизу) MPI-программы и гибридной MPI+OpenMP-программы. Характеристики вычислены относительно времени последовательной программы, откомпилированной без оптимизации (розовые и зеленые кривые) и с включенной оптимизацией -O2 (зеленые кривые)
Основные публикации:
К блоку 1:
- Shaidurov V. V., Shchepanovskaya G. I., Yakubovich M. V.
Numerical modelling of supersonic flows in channel // Russian J. of Numerical Analysis and Mathematical Modelling, 2012. — V. 27. — № 6. — P. 585–601 . - Щепановская Г. И.
Математическое и численное моделирование течений вязкого теплопровод ного газа // Вестник СибГАУ, 2011. — Т. 5. — № 38. — С. 101–106 . - Shchepanovskaya G.
Application of the trajectories method and the finite element method in modeling of viscous heat-conductive gas motion // Abst. of the «The 2nd Int. Conf. on Scientific Computing in Aerodynamics». — Beihang University, Beijing, P. R. China, 2012. — P. 50. - Шайдуров В. В., Щепановская Г. И., Якубович М. В.
Об условиях на границе расчетной области в методе конечных элементов // Материалы XVI Междунар. науч. конф. «Решетневские чтения», 2012. — С. 551–553 . - Шайдуров В. В., Щепановская Г. И., Якубович М. В.
Численное моделирование граничных условий в методе конечных элементов // Материалы всерос. науч. конф. «VII Всесибирский конгресс женщин-математиков». — Красноярск: СибГТУ, 2012. — С. 250–254 .
К блоку 2:
- Sadovskii V. M., Sadovskaya O. V.
Parallel Program Systems for Modeling Elastic-Plastic Waves in Structurally Inhomogeneous Materials [Электронный ресурс] / Numerical Analysis and Applied Mathematics: International Conference of Numerical Analysis and Applied Mathematics. Series: AIP Conference Proceedings, 2012. — V. 1479. — P. 1611–161 4. ISSN: 1551–761 6 (online). Режим доступа: http://proceedings.aip.org/resource/2/apcpcs/1479/1/1611_1. - Аннин Б. Д., Клунникова М. М., Садовская О. В., Садовский В. М.
Метод характеристик в задачах идеальной пластичности // ПММ, 2012. — Т. 76. — Вып. 5. — С. 867–877 . - Садовский В. М., Садовская О. В., Варыгина М. П.
Математическое моделирование волн маятникового типа с применением высокопроизводительных вычислений // Сб. тр. II Российско-Китайской науч. конф. «Нелинейные геомеханико-геодинамические процессы при отработке полезных ископаемых на больших глубинах». Новосибирск: ИГД СО РАН, 2012. — С. 138–144 .
К блоку 3:
- Karepova E., Dementyeva E.
The numerical solution of the inverse problem for shallow water models // Lecture Notes in Computer Science, 2013 (в печати). - Дементьева Е. В., Карепова Е. Д., Шайдуров В. В.
Восстановление граничной функции по данным наблюдений для задачи распространения поверхностных волн в акватории с открытой границей // Сибирский журнал индустриальной математики, 2013 (в печати).
(Отделы Вычислительной математики, Вычислительной механики деформируемых сред, Служба средств телекоммуникаций и вычислительной техники)
| К началу | |