| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2015 год
Важнейшие научные результаты ИВМ СО РАН 2015 года
- Важнейшие научные результаты ИВМ СО РАН 2015 года
- Программный комплекс теплового моделирования бортовой радиоэлектронной аппаратуры
- Автомодельное вырождение течения в осесимметричной затопленной турбулентной струе
- Модификация быстрого алгоритма шиарлет преобразования пространственных данных для решения задачи спектральной декомпозиции и эффективной визуализации сложных геообъектов
- Математическое моделирование оптического конфаймента ионных кулоновских кластеров
- Технология автоматизации проведения испытаний командно-измерительной системы космического аппарата
Программный комплекс теплового моделирования бортовой радиоэлектронной аппаратуры
Авторы: к.ф.-м.н. Деревянко В. А., к.ф.-м.н. Деревянко В. В., к.ф.-м.н. Нестеров Д. А. (научно-исследовательская группа отдела № 2 Вычислительной математики)
Разработан программный комплекс теплового моделирования бортовой радиоэлектронной аппаратуры (РЭА), предназначенный для теплового анализа электронного оборудования, создаваемого для космических аппаратов. Программный комплекс позволяет осуществлять автоматизированный расчет теплового режима бортовой аппаратуры, созданной с использованием теплоотводящих конструкций блоков на основе принципа фазовых переходов (с использованием плоских тепловых труб). В основе программного комплекса заложены математические модели тепловых процессов, разработанные в Институте. Пользователю программный комплекс предоставляет оконный графический интерфейс для определения параметров задачи, проведения расчетов и получения, визуализации и анализа результатов.
| К началу | |
Автомодельное вырождение течения в осесимметричной затопленной турбулентной струе
Автор: к.ф.-м.н. Шмидт А. В. (отдел № 4 Вычислительных моделей в гидрофизике)
Проведен основанный на теоретико-групповом анализе расчет течения в дальних областях осесимметричной затопленной турбулентной струи. Математическая модель включает дифференциальные уравнения на продольную и поперечную осредненную компоненту скорости, скорость диссипации энергии турбулентности, нормальные компоненты тензора рейнольдсовых напряжений, а также алгебраическую аппроксимацию Роди для касательного напряжения. Как видно из рисунка 1, результаты расчетов хорошо согласуются с известными экспериментальными данными.
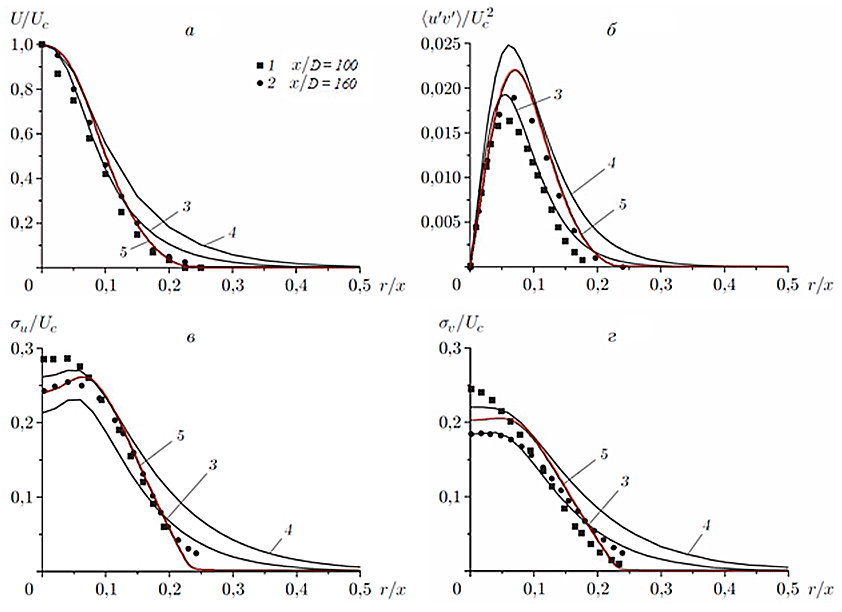
Рисунок 1. Сопоставление результатов расчетов (кривые 5) с экспериментальными данными (символы 1, 2) и результатами численного моделирования (кривые 3, 4): а) продольной осредненной компоненты скорости $U$; б) касательного рейнольдсова напряжения $\left\langle u'v'\right\rangle$; в), г) интенсивностей турбулентных флуктуаций компонент скорости $\sigma _{u} =\sqrt{\left\langle u'^{2} \right\rangle }$ и $\sigma _{v} =\sqrt{\left\langle v'^{2} \right\rangle }$, соответственно
Основные публикации:
- Шмидт А. В.
Автомодельное решение задачи о турбулентном течении круглой затопленной струи // ПМТФ. — 2015. — Т. 56, №3. — С. 82-88.
| К началу | |
Модификация быстрого алгоритма шиарлет преобразования пространственных данных для решения задачи спектральной декомпозиции и эффективной визуализации сложных геообъектов
Автор: д.т.н. Симонов К. В. (отдел № 5 Вычислительной механики деформируемых сред)
Исследование быстрого алгоритма шиарлет-преобразования пространственных данных FFST выявило, что контуры изучаемых объектов на изображениях можно получить как сумму коэффициентов шиарлет-преобразования фиксированного значения параметра для последнего (или определенного) масштаба и всевозможных значений параметра сдвига. В связи с этим предлагается использовать эту особенность при решении широкого круга прикладных задач по обработке и анализу данных комплексного геомониторинга природных явлений и процессов, рисунки 2 и 3.
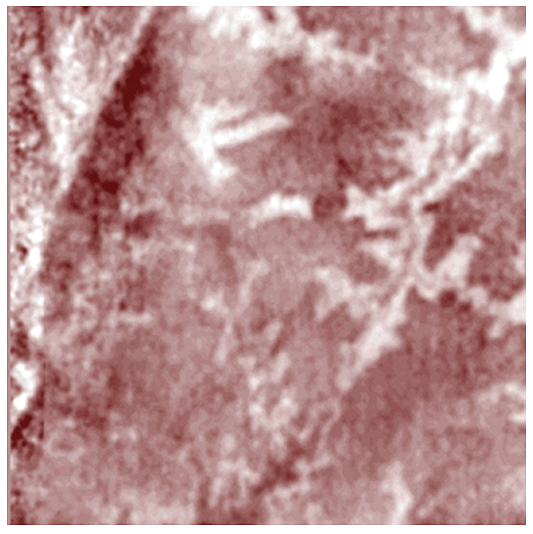
Рисунок 2. Пример данных сейсмической томографии: исходное изображение
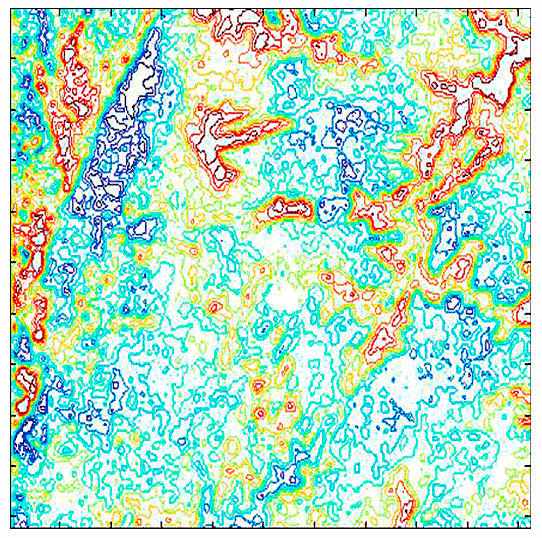
Рисунок 3. Пример расчета: спектральная декомпозиция данных и построение контура изучаемых геообъектов на основе модифицированного алгоритма шиарлет-преобразования.
Разработана следующая модификация алгоритма:
\[f_{cont} =\sum _{k=0}^{k_{\max } }\sum _{m=0}^{m_{\max } }sh_{\psi } \left(f(j*,k,m)\right), \]
где $sh_{\psi } $ — преобразование, которое ставит в соответствие исследуемой функции $f$ коэффициенты $sh_{\psi } \left(f(j*,k,m)\right)$, полученные для последнего (или заданного) масштаба $j*$, поворотов $k$ и смещений $m$; $k_{\max } $ — максимальное количество поворотов, $m_{\max } $ — максимальное количество смещений. В основу алгоритма положено дискретное быстрое прямое и обратное преобразования Фурье. В качестве материнского вейвлета в данной реализации используется вейвлет Мейера. Данная реализация алгоритма принимает на вход квадратные изображения, поскольку иначе возникают затруднения при обращении с коэффициентами на диагоналях.
Модифицированный алгоритм предлагается применять для спектральной декомпозиции и выделения соответствующего контура (края) исследуемого геообъекта. Успешные результаты решения этой задачи с помощью модифицированного алгоритма FFST показаны на различных данных (геоэкология, геодинамика, сейсмическая томография, следы природных катастроф). В таблице 1 приведены результаты расчетов для некоторых изображений и сравнение с фильтрами Собела (Sobel) и Превитта (Prewitt). Расчеты показали, что модифицированный алгоритм сравним по точности с классическими алгоритмами Собела и Превитта.
| Изображение (512х512) Модифицированный алгоритм FFST | Алгоритм Собела | (Sobel) | Алгоритм Превитта (Prewitt) |
|---|---|---|---|
| Данные томографии | 27.05942 | 27.00415 | 27.00416 |
| Данные геоэкологии | 24.24514 | 24.19391 | 24.19392 |
| Данные картографии | 24.09939 | 24.09939 | 24.09939 |
| Данные спутника AQUA (появления пожара) | 24.10199 | 24.10134 | 24.10134 |
| Данные спутника AQUA (появления пожара) | 24.10234 | 24.10215 | 24.10215 |
| Данные спутника NPP (появления пожара) | 24.10220 | 24.10188 | 24.10188 |
Таблица 1. Значение метрик PSNR (dB) при решении задачи выделения контура для различных изображений
Основные публикации:
- Simonov K. V., Kurako M. A.
Computer technology for data processing of complex monitoring of natural geoobjects // Совместный выпуск. Вычислительные технологии, том 20. Вестник КАЗНУ им. Аль-Фараби, серия: математика, механика и информатика, № 3 (86), часть I. Алматы — Новосибирск, 2015. С. 294–299 . - Бодякин Е. В., Перетокин С. А., Симонов К. В.
Методика проведения сейсмического микрорайонирования площадок с использованием ГИС технологий // Информатизация и связь. — 2015. — № 2. — C. 80-83.
| К началу | |
Математическое моделирование оптического конфаймента ионных кулоновских кластеров
Авторы: д.ф.-м.н. И. В. Краснов, к.ф.-м.н. Л. П. Каменщиков (отдел № 7 Вычислительной физики)
На основе теоретического анализа и компьютерного моделирования движения ионов в резонансном световом поле предложено решение проблемы полностью оптического получения и удержания холодных кулоновских кластеров. Новый метод основан на использовании выпрямленных градиентных сил, действующих на ионы в 3D полихроматической диссипативной оптической сверхрешётке (ДОС), и свободен от нежелательных эффектов, присущих традиционным ионным ловушкам (типа нагрева ионов из-за микро-осцилляций в радиочастотных ловушках Паули). Проведённые компьютерные расчёты стохастической динамики ионов иттербия в ДОС предсказывают образование ионных кулоновских кластеров с температурой ≈ 10−3 K и временем жизни десятки секунд при интенсивности оптических полей, не превышающих нескольких Вт/см2.
Решение системы стохастических дифференциальных уравнений и различных функционалов от решения (время жизни кластера, температура и т.п.) оценивается как выборочное среднее от $N$ независимых частных решений $\varphi_{i}$, при этом величина $N$, исходя из соображения точности оценки, берется в данной конкретной задаче порядка $10^{4} {\kern 1pt} -{\kern 1pt} {\kern 1pt} 10^{6} $. Каждая отдельная реализация $\varphi _{i} $ вычисляется достаточно долго из-за большой сложности правой части системы уравнений. Поэтому численное исследование таких систем уравнений возможно только на основе методики распараллеливания с использованием суперкомпьютеров. Типичное время расчета одного варианта для $N=10^{5}$ и при $10^{7}$ шагах по времени на суперкомпьютере МВС-100 (в МСЦ РАН) составляет 12-24 часа на 2
Основные публикации:
- Krasnov I. V.
Conditions for formation and trapping of the two-ion Coulomb cluster in the dissipative optical superlattice // Chinese Physics B, 24, 063701- (1-9) (2015). - Krasnov I. V., Kamenshchikov L. P.
Ions in the cell of the dissipative optical superlattice: cooling trapping and Coulomb cluster formation // Laser Physics, 25 (11), 115501 — (1-8) (2015). - Krasnov I. V., Kamenshchikov L. P.
All-optical trapping of strongly coupled ions // Optics Communications 312, 192–198 (2014). - Krasnov I. V.
Three-dimensional localization of atoms in the polychromatic optical superlattice // Physics Letters A. 375, 2471–247 8 (2011).
| К началу | |
Технология автоматизации проведения испытаний командно-измерительной системы космического аппарата
Авторы: д.т.н. Ноженкова Л. Ф., к.т.н. Исаева О. С., к.т.н. Евсюков А. А., Вогоровский Р. В., Грузенко Е. А., Колдырев А. Ю. (отдел № 8 Прикладной информатики)
Совместно с СФУ и АО «Информационные спутниковые системы им. академика М. Ф. Решетнева» разработана технология проведения испытаний бортовой аппаратуры командно-измерительной системы космических аппаратов. Технология позволяет организовать взаимодействие программного обеспечения с контрольно-проверочной аппаратурой. Разработано программное обеспечение для управления работой оборудования в соответствии с заданным сценарием. Использование новой технологии позволяет ускорить и существенно удешевить испытания бортовых комплексов.
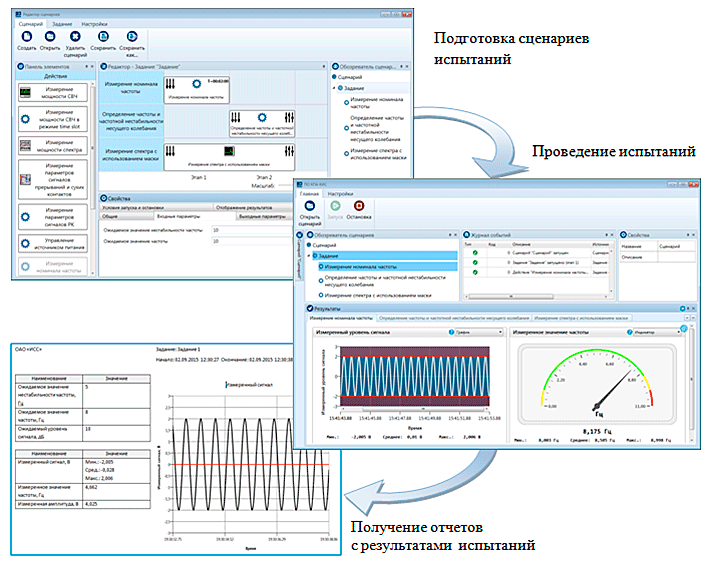
Рисунок 8. Визуализация технологии
Основные публикации:
- Ноженкова Л. Ф., Исаева О. С., Вогоровский Р. В.
Подготовка и проведение испытаний бортовой аппаратуры командно-измерительной системы космического аппарата // Исследования наукограда. — 2015. — № 1(14). — С. 60-67. - Ноженкова Л. Ф., Исаева О. С., Грузенко Е. А., Вогоровский Р. В., Колдырев А. Ю., Евсюков А. А.
Комплексная поддержка конструирования бортовых систем контроля и управления космических аппаратов на основе интеллектуальной имитационной модели // Информационные технологии. — 2015. — № 9. — С. 706–714 . - Исаева О. С., Грузенко Е. А., Вогоровский Р. В., Колдырев А. Ю.
Моделирование и анализ функционирования бортовой аппаратуры командно-измерительной системы космического аппарата // Информатизация и связь. — 2015. — № 1. — С. 58-64. - Вогоровский Р. В.
Организация взаимодействия с измерительным оборудованием при проведении испытаний бортовой аппаратуры КА // Молодой ученый. — 2015. — № 11. — С. 22-27.
| К началу | |