| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 1998 год
Программы фундаментальных исследований Сибирского Отделения Российской Академии Наук
- Программы фундаментальных исследований Сибирского Отделения Российской Академии Наук
- Программа 5."Математическое моделирование,информационные технологии и вычислительная техника"
- Тема: «Математическое моделирование движений жидкости с поверхностями раздела, гидротермических процессов».
- Тема: «Математическое моделирование управляющих воздействий резонансных лазерных полей на атомы и ионы с целью создания плазменных и газовых состояний с заданными физическими свойствами».
- Тема: «Построение математической модели магнитопаузы и плазменного слоя магнитосферы Земли с учетом неустойчивостей диссипативных процессов».
- Тема: «Разработка теоретических основ газодинамического конструирования».
- Тема: «Разработка вычислительных методов для решения упругопластических контактных задач».
- Тема: «Методы построения и анализа динамических моделей неравновесных физико-химических систем».
- Тема: «Алгоритмы и программы нейросетевой обработки данных».
- Тема: «Развитие методов ресурсного проектирования и оценки безопасности технических систем и потенциально опасных объектов».
- Тема: «Разработка математического и программного обеспечения многоуровневых интеллектуальных информационных систем принятия решений».
Программа 5."Математическое моделирование,информационные технологии и вычислительная техника"
Тема: «Математическое моделирование движений жидкости с поверхностями раздела, гидротермических процессов».
№ гос. регистрации 01.96 0.0 05368.
Научный руководитель -
д.ф.-м.н., проф. Андреев В. К..
Исследована устойчивость нестационарных течений цилиндрического и плоского слоев, когда внутренний слой является поверхностью раздела, а внешний — свободной границей. Найдена эволюция возмущений поверхностей в зависимости от отношения плотностей жидкости, толщины и числа Вебера. Проведены численные расчеты для конкретных расплавов (Андреев В. К.).
Даны априорные оценки решения малых возмущений покоя в новой модели микроконвекции (Андреев В. К., Бекежанова В. Б.).
В случае подогрева снизу исследованы условия возникновения конвекции с учетом термодиффузии (эффект Соре) для плоского горизонтального слоя вязкой теплопроводной жидкости. Оказалось, что эффект Соре приводит к дестабилизации покоя; построены численно нейтральные кривые устойчивости (Рябицкий Е. А.).
Разработана трехмерная дискретная модель несжимаемой жидкости для расчета взаимодействия струй несжимаемой жидкости с телами, в том числе подвижными. Она применена к решению задачи о подвешивании шара в вертикальной струе жидкости. Модель позволила численно получить эффект устойчивых колебательных движений шара в струе, а также получить количественные зависимости периода колебаний от ширины струи и плотности шара (Франк А. М.).
Для описания переноса и превращения примесей в турбулентном потоке несжимаемой жидкости применяется одномерное уравнение переноса. Выбрана параметризация расхода взмыва-осаждения в турбулентном потоке.
Разработаны численные алгоритмы и программы для определения концентраций примесей в речных потоках с учетом седиментации и взмучивания. Выполнены тестовые расчеты (Рис.) (Белолипецкий В. М.).
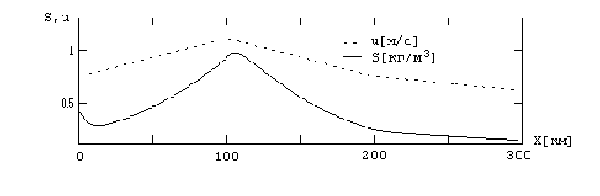
Изменение концентрации примеси в воде с учетом взмучивания и осаждения (d=0.1 мм — характерный размер частиц)
:
- Захватаев В. Е.
О волновых движениях в тонком слое вязкой жидкости. Влияние постоянного электрического поля // ПМТФ. — 1998. — Т. 30. — № 1. — С. 90-97. - Андреев В. К.
Развитие тепловой конвекции в одной моделимикрогравитации // Тезисы ИНПРИМ-98, Ч. 2. — Новосибирск, 1998. — С. 82. - Белолипецкий В. М., Генова С. Н., Гуревич К. Ю., Знаменский В. А., Компаниец Л. А., Якубайлик Т. В.
Наблюдения за экологическим состоянием бассейна реки Енисей при помощи новых информационных технологий // ГИС для оптимизации природопользования в целях устойчивого развития территорий: Материалы международной конференции. — Барнаул: Изд-во Алтайского гос. ун-та, 1998. — С. 490–498 . - Frank A. M.
3D discrete simulation of a liquid jet suspending a ball // Proc. of 6th Japan-Russia Simp. on CFD. — Nagoya, Japan, 1998. — P. 117–120 .
| К началу | |
Тема: «Математическое моделирование управляющих воздействий резонансных лазерных полей на атомы и ионы с целью создания плазменных и газовых состояний с заданными физическими свойствами».
№ гос. регистрации 01.96 0.0 05369.
Научный руководитель -
д.ф.-м.н., проф. Шапарев Н. Я..
Построена математическая модель процесса охлаждения резонансных ионов в плазме как в отсутствии СВЧ нагрева электронов, так и в присутствии. Предварительные расчеты показали, что в первом случае возможно создание неидеальной (параметр неидеальности больше 10) разреженной плазмы, а во втором — достижение условий (в режиме адиабатического сканирования частоты охлаждающего резонансного лазерного излучения) близких к условиям вигнеровской кристаллизации плазмы (Гаврилюк А. П., Краснов И. В., Шапарев Н. Я.).
Построена модель взаимодействия оптической мембраны (ОМ) с потоком газа, содержащего малую примесь резонансных атомов. На основе ее показана возможность значительного увеличения концентрации (на несколько порядков) резонансных атомов в области локализации ОМ. (Гаврилюк А. П., Краснов И. В., Полютов С. П., Шапарев Н. Я.).
:
- Gavriluk A. P., Krasnov I. V., Shaparev N. Ya.
Lazer cooling and Wigner crystallization of rarefied plasma // Physics of vibrations. — 1998. — V. 6. — № 1. — P. 67-74. - Gavriluk A. P., Krasnov I. V., Shaparev N. Ya.
Laser cooling and Wigner crystallization of resonant plasma in magneto-optical trap // Proceedings of the second International Symposium on Modern Problems of Laser Physics. — Novosibirsk. — 1998. — Vol. 1. — P. 317–325 .
| К началу | |
Тема: «Построение математической модели магнитопаузы и плазменного слоя магнитосферы Земли с учетом неустойчивостей диссипативных процессов».
№ гос. регистрации 01.96 0.0 05370.
Научные руководители — д.ф.-м.н. Денисенко В. В., д.ф.-м.н. Еркаев Н. В..
Рассчитано распределение электрического потенциала на магнитопаузе, в плазменном слое и на уровне ионосферы при заданном на основе экспериментальных данных распределении скорости течения в плазменном слое (Денисенко В. В., Китаев А. В.).
Предложен вариационный принцип для трехмерной задачи теплопроводности в движущейся среде (Денисенко В. В.).
Выполнено численное исследование трехмерной МГД модели обтекания затупленного тела с учетом анизотропии давления и температуры газа (Еркаев Н. В.).
:
- Денисенко В. В., Китаев А. В.
Математическое моделирование ионосферных электрических полей, возбуждаемых в магнитосфере Земли // Тезисы докладов Третьего Сибирского конгресса по прикладной и индустриальной математике. — Ч. 2. — Новосибирск, 1998. — С. 95-96. - Denissenko V. V.
The energy method for boundary value problems of transfer in moving medium / Proceedings of the 4th International Conference on Information Systems, Analysis and Synthesis. — V. 2. — Orlando, US. — 1998. — P. 347–351 .
| К началу | |
Тема: «Разработка теоретических основ газодинамического конструирования».
№ гос. регистрации 01.96 0.0 05371.
Научный руководитель -
д.ф.-м.н. Щепановский В. А..
Газодинамическое констpуиpование с его оpиентацией на нелинейные и тpехмеpные пpоблемы позволяет постpоить течение в пpостpанстве тpех измеpений, базиpующееся на частных pешениях уpавнений газовой динамики. Пpи постановке задач вязкого обтекания в качестве гpаничного условия входит pешение обтекания идеальным газом того же тела. Газодинамическое констpуиpование с высокой точностью задания гpаничного условия дает возможность снизить тpебования к математической вязкой модели и получить качественно новые pезультаты (Щепановский В. А., Щепановская Г. И.).
Получена математическая модель нестационаpных pежимов пpоцессов pазделения компонентов, отсутствующих в остатке и pектификате. Пpи этом учитывается наличие неpаспpеделяющихся компонентов в pециpкуляционных потоках. Данное обстоятельство пpиводит к кpаевым задачам, у котоpых гpаничные условия содеpжат обыкновенные диффеpенциальные уpавнения. Пpоведен численный экспеpимент для пpомышленных установок pазделения многокомпонентных смесей (Демиденко Н. Д.).
:
- Щепановский В. А., Щепановская Г. И.
Газодинамическое констpуиpование в пpоблеме сопpотивления. — Новосибиpск: Наука. — 1998. — 316 c. - Shchepanovskii V. A.and Shchepanovskaya G. I.
Three — dimensional solution for supersonic aerodynamics // International journal of Computational fluid dynamics. — 1998. — Vol. 10. — P. 127–137 .
| К началу | |
Тема: «Разработка вычислительных методов для решения упругопластических контактных задач».
№ гос. регистрации 01.96 0.0 05372.
Научный руководитель -
д.ф.-м.н., проф. Садовский В. М..
Построены и обоснованы новые разностные схемы решения одномерных и двумерных задач динамики слоисто-неоднородных упругих и упругопластических сред, обладающие рядом преимуществ перед известными схемами. Эти преимущества выражаются в высокой точности описания разрывов решения, монотонности, отсутствии иных нефизичных эффектов (Садовский В. М., Богульский И. О.).
Разработаны алгоритмы и программы моделирования отраженных монотипных и обменных волн с различными упругими свойствами. На модели, типичной для осадочной толщи Западной Сибири, получены сейсмограммы, которые использованы для решения обратных динамических задач с целью определения акустических жесткостей и скоростей пробега поперечных волн (Кочнев В. А., Гоз И. В.).
:
- Бычек О. В., Садовский В. М.
К исследованию динамического контактного взаимодействия деформируемых тел // ПМТФ. — 1998. — Т. 39. — № 4. — С. 167–173 . - Богульский И. О., Ветров С. Я., Шабанов А. В.
Электромагнитные волны в неограниченных и конечных сверхрешетках // Оптика и спектроскопия. — 1998. — Т. 84. — № 5. — С. 823–828 . - Гоз И. В.
Некоторые результаты обработки синтетических сейсмограмм метода ВСП ПБ // Деп. в ВИНИТИ 12.02.98; № 416-В98.
| К началу | |
Тема: «Методы построения и анализа динамических моделей неравновесных физико-химических систем».
№ гос. регистрации 01.96 0.0 05372.
Научные руководители:
д.ф.-м.н., проф. Горбань А. Н., д.ф.-м.н., проф.
Быков В. И..
Построены кинетические уравнения, последовательно исправляющие моментные приближения в теории уравнения Больцмана. Решена проблема конструктивного построения равновесий в моделях решеточной кинетики. Построена техника регуляризации разложений и операционное исчисление для переопределенных полных систем функций.
:
- Karlin I. V., Gorban A. N., Dukek G., Nonnenmacher T. F.
Dynamic correction to moment approximation // Physical Review E. — 1998. — V. 57. — № 2. — P. 1669–167 2. - Karlin I. V., Gorban A. N., Succi S., Boffi V.
Maximum Entropy Principle for Lattice Kinetic Equation // Physical Review Letters. — 1998. — V. 81. — № 1. — P. 6-9. - Gorban A. N., Karlin I. V.
r operator in a overfull set // Europhys. Lett. — 1998. — V. 42. — № 2. — P. 113–117 .
| К началу | |
Тема: «Алгоритмы и программы нейросетевой обработки данных».
№ гос. регистрации 01.96 0.0 05376.
Научный руководитель -
д.ф.-м.н., проф. Горбань А. Н..
Построены методы нейросетевого представления знаний и их вербализации. создано соответствующее программное обеспечение. Исследованы вычислительные возможности искусственных нейронных сетей. Заново рассмотрен классический вопрос о представлении функций многих переменных с помощью суперпозиций и сумм функций одного переменного. Показано, что можно получить сколь угодно точное приближение любой непрерывной функции многих переменных, используя операции сложения и умножения на число, суперпозицию функций, линейные функции а также одну произвольную непрерывную нелинейную функцию одной переменной. Для нейронных сетей полученные результаты означают: от функции активации нейрона требуется только нелинейность. Показано, что для любой непрерывной функции многих переменных можно построить нейронную сеть, которая вычисляет ее с любой заданной точностью.
:
- Горбань А. Н.
Обобщенная аппроксимационная теорема и вычислительные возможности нейронных сетей // Сибирский журнал вычислительной математики. — 1998. — Т. 1. — № 1. — С. 12-24. - Миркес Е. М.
Нейрокомпьютер: проект стандарта. — Новосибирск: Наука. — 1998. — 343 c.
| К началу | |
Тема: «Развитие методов ресурсного проектирования и оценки безопасности технических систем и потенциально опасных объектов».
№ гос. регистрации 01.96 0.0 05381.
Научный руководитель -
д.т.н., проф. Москвичев В. В..
На основе теоретического анализа процессов зарождения и развития повреждений в элементах конструкций дана концептуальная формулировка остаточного ресурса потенциально опасных объектов. В основе формулировки положено понятие «безопасное повреждение». В качестве повреждений рассматриваются технологические и эксплуатационные дефекты типа трещин. Остаточный ресурс определяется как интервал времени, в течение которого выявленные в процессе технической диагностики дефекты и трещины остаются в безопасных пределах. С указанной концептуальной позиции рассмотрена проблема оценки остаточного ресурса конструкций и предложены методы ее решения. Количественные оценки остаточного ресурса основаны на диффузионных, скачкообразных или диффузионно-скачкообразных модельных представлениях процесса роста повреждений. Особое внимание уделяется учету вероятностных свойств исходных повреждений, процессов нагружения и характеристик материалов. Начальное повреждение рассматривается как событие пуассоновского типа. Получили дальнейшее развитие разработанные ранее методы численного моделирования кинетики повреждений. Проведены численные статистические эксперименты для оценки рассеяний характеристик напряженно-деформированного состояния в вершине растущей трещины. На этой основе развиты вероятностные описания параметров напряженно-деформированного состояния и критериев разрушения. Разработана первая версия автоматизированной системы оценки остаточного ресурса конструкций с повреждениями. Система выполняет расчет напряженно-деформированного состояния в области повреждений, определяет критические параметры напряженного состояния и вероятностные оценки остаточного ресурса. При этом ведется архив результатов расчетов с целью накопления базы данных по особенностям и условиям разрушений.
:
- Москвичев В. В., Доронин С. В.
Нормирование долговечности и дефектности сварных конструкций // Проблемы машиностроения и надежности машин. — 1998. — № 1. — С. 44-49.
| К началу | |
Тема: «Разработка математического и программного обеспечения многоуровневых интеллектуальных информационных систем принятия решений».
№ гос. регистрации 01.9.80. 007505.
Научные руководители:
д.т.н., проф. Лапко А. В., к.т.н. Ноженкова Л. Ф..
Разработаны самообучающиеся непараметрические методы и программные средства поиска относительного глобального экстремума, основанные на декомпозиции и кусочной аппроксимации целевой функции с помощью алгоритмов автоматической классификации с последующим решением задач локальной оптимизации и сравнением их результатов.
Предлагаемые методы впервые формализуют задачу оптимизации статических систем при неполной информации и на порядок превышают вычислительную эффективность традиционных непараметрических процедур поиска экстремума (Лапко А. В., Ченцов С. В.).
Проведены исследования по развитию фреймово-продукционного подхода для перехода от функционально-технологического к модельному уровню интеграции в программных системах и созданию средств проектирования интеллектуальных геоинформационных систем. Разработанная модель ориентирована на автоматизацию процессов формирования семантических, картографических запросов, операций генерализации и семантическую интерпретацию пространственной информации. Выполнены исследования по применению других методов построения интеллектуальных систем для представления и применения гибридных методов в экспертных геоинформационных системах, в том числе исследование нечетких моделей представления знаний для решения задач прогнозирования в ГИС и апробирование технологий нейронных сетей для решения задач территориального зонирования. Для повышения уровня интеграции с базами данных и знаний выполнялись работы по развитию алгоритмических и программных средств визуализации в ГИС ( Ноженкова Л. Ф.).
:
- Lapko A. V., Cheremnov S. A.
Nonparametric Classification Methods in Problem of Optimization of Statistical Systems // Pattern Recognition and Image Analysis. — 1998. — Vol. 8. — P. 133–134 . - Лапко А. В., Черемнов С. А.
Непараметрические методы классификации в задачах оптимизации статических систем // Тезисы докладов 3 Всероссийской конференции с международным участием «Распознавание образов и анализ изображений: новые информационные технологии». — Нижний Новгород, 1997. — С. 49-51. - Исаев С. В., Карев В. Ю., Нейман К. А.
Инструментальные средства ГИС для построения интегрированных информационных систем / ГИС для оптимизации природопользования в целях устойчивого развития территорий: материалы Международной конференции «Интеркарто-98». — Барнаул: Изд-во Алтайского гос. ун-та. — 1998. — C. 139–145 . - Исаев С. В.
Проблемы создания ГИС-приложений в интегрированных информационных системах / Материалы конференции молодых ученых Института вычислительного моделирования СО РАН. — Красноярск: ИВМ СО РАН, 1998. — C. 15-23. - Ноженкова Л. Ф., Родионова О. С.
Построение нечеткой модели для прогнозирования пожарной опасности лесов / Нейроинформатика и ее приложения: Тезисы докладов VI Всероссийского семинара. — Красноярск: КГТУ, 1998. — C. 130–131 .
| К началу | |