| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2004 год
Гранты российских научных фондов
- Гранты российских научных фондов
- Грант Президента РФ № МК-143.2003.01 «Разработка теоретических основ построения непараметрических моделей коллективного типа в задачах восстановления стохастических зависимостей»
- Грант Президента РФ № МК-982.2004.1 «Математическое и численное моделирование процессов распространения упругопластических волн в сыпучей среде»
- Грант РФФИ №
02–01–00 078 — «Бесконечные группы с различными условиями конечности» - Грант РФФИ №
02–01–00 523 — «Математическое и численное моделирование нестационарного распространения импульса энергии большой мощности в вязком теплопроводном газе» - Грант РФФИ №
02–01–00 934 «Устойчивость термодиффузионных течений жидкости с поверхностью раздела» - Грант РФФИ №
02–07–90 135 — «Создание Красноярской сети параллельных вычислений» - Грант РФФИ №
03–01–00 218 «Трехмерное численное моделирование термокапиллярной неустойчивости в тонких слоях жидкости со свободной границей» - Грант РФФИ
03–05–20 014 БНТС-а — «Нестационарная магнитогидродинамика тонких магнитных трубок в магнитосфере» - Грант РФФИ №
04–01–00 130 «Симметрии, инварианты и дифференциальные связи уравнений с частными производными» - Грант РФФИ №
04–01–00 267 — «Разработка математических моделей и методов расчета задач механики реологически сложных сыпучих сред» - Грант РФФИ №
04–05–64 088 — «Математическое моделирование магнито-сферных МГД генераторов» - Грант РФФИ № 902.2003.1 — ведущие научные школы — «Теория и приложения задач со свободной границей»
- Грант РФФИ №
04–05–78 038д — «Издание монографии «Методы светорассеяния в анализе водных дисперсных биологических сред"" - Грант РФФИ №
04–01–10 030 — «Организация и проведение III Всесибирского конгресса женщин-математиков» - Грант РФФИ №
04–07–93 024-г — «Организация и проведение IV Межрегиональной школы-семинара «Распределенные и кластерные вычисления"" - Грант РГНФ №
03–05–12 012в «Разработка территориально распределённой информационной системы эпидемиологического мониторинга артериальной гипертонии среди населения региона»
Грант Президента РФ № МК-143.2003.01 «Разработка теоретических основ построения непараметрических моделей коллективного типа в задачах восстановления стохастических зависимостей»
Руководитель:
к.т.н., доцент В. А. Лапко
Разработаны и исследованы непараметрические модели пространственно распределённых временных систем в неоднородных условиях, определены их асимптотические свойства. Создана методика оценивания показателей эффективности моделей. Проведены вычислительные эксперименты для исследования свойств моделей при конечных объёмах обучающих выборок.
Основные публикации:
- Лапко В. А., Молоков В. В., Лапко А. А.
Модификации непараметрических моделей коллективного типа в задачах восстановления временных процессов // Вестник КрасГАУ. — 2003. — № 3. — С. 44-49. - Лапко В. А., Соколов М. И., Цугленок Г. И.
Статистические модели электротехнических изделий и процессов с учётом их частичного описания // Вестник КрасГАУ. — 2003. — № 3. — С. 267–269 . - Лапко В. А.
Синтез и анализ гибридных моделей стохастических зависимостей в условиях наличия их частного описания // Автометрия. — 2004. — № 1. — С. 51-59.
(Отдел вычислительной математики)
| К началу | |
Грант Президента РФ № МК-982.2004.1 «Математическое и численное моделирование процессов распространения упругопластических волн в сыпучей среде»
Руководитель:
к.ф.-м.н. О. В. Садовская
На основе методов расщепления по физическим процессам и по пространственным переменным разработаны параллельные вычислительные алгоритмы для исследования задач динамики сыпучей среды с учетом упругих и пластических деформаций. К решению одномерных задач применена явная по времени монотонная ENO — схема с предельной реконструкцией решения в сочетании с процедурой корректировки, учитывающей пластичность. Распараллеливание вычислительного процесса осуществлено на этапе расщепления по пространственным переменным. На многопроцессорных вычислительных системах серии МВС-1000 проведены двумерные расчеты распространения ударных волн сжатия (сигнотонов) в разрыхленной сыпучей среде.
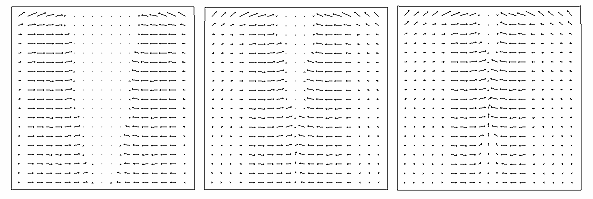
Рис. 1. Поле скоростей в задаче кумулятивного взаимодействия сигнотонов.
Основные публикации:
- Садовская О. В.
Метод сквозного счета для исследования упругопластических волн в сыпучей среде // Журнал вычислительной математики и математической физики. — 2004. — Т. 44. — № 10. — С. 1909–192 0. - Sadovskaya O. V., Sadovskii V. M.
Mathematical and Numerical Modeling of Elastic-Plastic Waves in Granular Materials // 21st Int. Сongress of Theoretical and Applied Mechanics. Abstr. Book and CD-ROM Proceedings. — Warsaw. — Poland. — 2004. — P. 279. - Sadovskii V. M., Sadovskaya O. V.
Mathematical Modeling of the Granular Medium Dynamics on Multiprocessor Computing Systems // VI Int. Congress on Mathematical Modeling. Book of Abstr. — N. Novgorod. — 2004. — P. 338.
(Отдел вычислительной механики деформируемых сред)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. В. П. Шунков
Получен признак непростоты бесконечной группы, содержащей бесконечную систему подгрупп Фробениуса с неинвариантным множителем SL2(3). Охарактеризованы Mp-группы с р-конечной ручкой произвольного простого порядка, отличного от трех. Построен контр-пример к характеризационной теореме группы, для которой не выполняется одно из условий теоремы и утверждение теоремы. Продолжалось изучение групп с почти слойно конечной периодической частью: получено описание силовских 2-подгрупп и некоторых двупорожденных подгрупп.
Основные публикации:
- Козулин С. Н., Сенашов В. И., Шунков В. П.
Группы с ручками порядка, отличного от трех // Укр. мат. журнал. — 2004. — Т. 56. — № 8. — С. 1030–104 2. - Козулин С. Н., Сенашов В. И., Шунков В. П.
О бесконечных группах Фробениуса // Красноярск: ИВМ СО РАН. — 2004. — 16 с. (Деп. в ВИНИТИ 31.03.05, № 536-В2004). - Козулин С. Н.
Характеризация Мр-групп // Материалы конф. молодых ученых ИВМ СО РАН. — Красноярск: ИВМ СО РАН. — 2004. — С. 23-24. - Козулин С. Н.
Бесконечные группы с группами Фробениуса // Препринт № 2. — Красноярск: ИВМ СО РАН. — 2004. — 17 с. - Тимофеенко А. В.
О строго вещественных элементах конечных групп // Материалы междунар. конф. «Алгебра, логика и кибернетика». — Иркутск: Изд-во ГОУ ВПО Иркутского гос. пед. ун-та. — 2004. — С. 104–105 .
(Отдел дискретной математики)
| К началу | |
Грант РФФИ №
Руководитель:
чл.-корр. РАН В. В. Шайдуров
Создана математическая модель, описывающая двумерные и трехмерные сверх- гиперзвуковые течения вязкого теплопроводного газа с сильными неоднородностями. Выписаны нелинейные уравнения в частных производных, определяющие законы сохранения массы, импульса и энергии с учетом тепловых и диссипативных потерь.
Исследован как теоретически, так и численно новый тип краевых условий на границе расчетной области. Получены краевые условия, сохраняющие сеточные аналоги балансовых соотношений для энергии, которые проявляют себя как неотражающие, т.е. без искажений пропускают возмущения среды из расчетной области наружу без какого-либо влияния на значения решения внутри области.
Разработано программное обеспечение на многопроцессорной вычислительной системе МВС 1000/16 для решения комплекса задач с несколькими неоднородностями в вязком теплопроводном газе (Г. И. Щепановская).
Рассмотрена аппроксимация двумерной задачи Навье-Стокса по пространству методом конечных элементов. Использованная постановка задачи отличается краевыми условиями на границе расчетной области, связывающими производные скоростей и давление. Эти краевые условия являются естественными для вариационной (интегральной) постановки, т.е. не накладывают дополнительных условий на подпространства пробных и тестовых функций в отличие от главных краевых условий (типа условий Дирихле).
Для аппроксимации по пространству использован метод Бубнова-Галеркина в комбинации с методом линий. В качестве пространства пробных и тестовых функций использовано пространство функций, кусочно-билинейных на квадратных ячейках. Для вычисления интегралов по элементарным областям использована квадратурная формула метода трапеций и его двумерного аналога как декартова произведения.
В итоге получена система обыкновенных дифференциальных уравнений по времени относительно четырех векторов, состоящих из значений плотности, скоростей и энергии в узлах квадратной сетки и зависящих от времени.
Для дискретного аналога доказаны некоторые полезные свойства — дискретные аналоги непрерывных балансовых соотношений, такие как сохранение массы и полной энергии. (Е. Д. Карепова).
Основные публикации:
- Карепова Е. Д., Малышев А. В., Шайдуров В. В.
Метод конечных элементов для уравнений Навье-Стокса вязкого теплопроводного газа // Тр. междунар. конф. по вычислительной математике МКВМ-2004 — Новосибирск. — 2004. — Т. 2. — С. 503–510 . - Карепова Е. Д., Шайдуров В. В.
Численное решение уравнений Навье-Стокса вязкого теплопроводного газа. Часть II. Аппроксимация по пространству методом конечных элементов // Красноярск: ИВМ СО РАН. — 2004. — 70 с. (Деп. в ВИНИТИ 13.01.04, № 58-В2004). - Шайдуров В. В., Щепановская Г. И.
К вопросу о снижении плотности в набегающем потоке перед летательным аппаратом // Тр. VIII Всерос. науч. конф. «Решетневские чтения». — Красноярск: СибГАУ. — 2004. — С. 23-24. - Шайдуров В. В., Щепановская Г. И.
Метод четвертого порядка точности для уравнения переноса с переменными коэффициентами // Вестник КрасГУ. — 2004. — Вып. 3. — С. 154–159 . - Шайдуров В. В., Щепановская Г. И.
Вычислительное моделирование сильных неоднородностей в вязком теплопроводном газе // Вычислительные технологии. — 2004. — Вестник КазНУ. — № 3(42). — (Совм. выпуск. — Ч. 4). — С. 280–287 .
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. В. К. Андреев
Для уравнений неизотермических плоских движений бинарных смесей найдены оптимальные системы подалгебр всех порядков. Построены новые точные решения, описывающие стационарные течения в плоских слоях под разными углами к силе тяжести. Численными и аналитическими методами определено влияние эффекта Соре на развитие нестационарных течений в плоском и цилиндрических (В. К. Андреев, А. Е. Картошкина, Н. Л. Собачкина, А. А. Родионов).
Основные публикации:
- Андреев В. К., Картошкина А. Е.
О движении плоского слоя жидкости со свободной границей под действием эффекта Соре // Вестник КрасГУ. — 2004. — Вып. 1. — С. 182–191 . - Андреев В. К., Собачкина Н. Л.
Нестационарное растяжение жидкого цилиндра под действием эффекта Соре // Вестник КрасГУ. — 2004. — Вып. 1. — С. 192–202 . - Андреев В. К., Бекежанова В. Б.
Об устойчивости стационарного течения в вертикальном слое в модели микроконвекции // МЖГ. — 2004. — № 2. — С. 57-68. - Андреев В. К., Рябицкий Е. А.
Возникновение микроконвекции в плоском слое со свободной границей // ПМТФ. — 2004. — Т. 45. — № 1. — С. 29-38. - Андреев В. К., Рыжков И. И.
Групповые свойства уравнений термодиффузии в плоском случае // Тр. математического центра им. Н. И. Лобачевского. — Казань: Казанское мат. общ-во. — 2004. — С. 11-18.
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ №
Руководитель:
чл.-корр. РАН В. В. Шайдуров
В течение года производилось техническое обслуживание и администрирование кластера МВС-1000/16, в том числе:
- выполнены ремонты одного из коммутаторов и радиатора процессора управляющего узла;
- увеличена емкость основного жесткого диска управляющего узла;
- заведено новых пользователей — 6, из них сотрудников сторонних учебно-научных организаций — 4.
В настоящее время на кластере зарегистрировано 25 пользователей.
Ориентировочно средняя суммарная загрузка вычислительных узлов кластера составляет 40-50%. С учетом резервирования 5-ти узлов из имеющихся 15 под отладочные задачи, загрузка близка к максимально возможной.
В течение года производились консультации пользователей и решались проблемы неадекватного функционирования кластера, связанного с неисправностями оборудования или настройкой программного обеспечения.
Одной из главных задач в настоящее время является обучение и отладка параллельных программ, которые затем (в связи с недостаточной производительностью МВС-1000/16) могут запускаться на кластере МВС-1000М Межведомственного суперкомпьютерного центра. Он имеет полностью совместимое программное обеспечение и систему запуска задач как у МВС-1000/16, но существенно большую мощность. Институт координирует подключение пользователей КНЦ СО РАН к этому кластеру. В настоящее время там зарегистрировано 7 пользователей, работающих над четырьмя проектами.
С целью создания более производительного вычислительного кластера проведено исследование архитектуры и конструктивных решений современных многомашинных систем. Сделаны выводы по соотношению цены и производительности и разработаны конструктивные решения по созданию в ИВМ СО РАН кластера на основе 24 вычислительных и одного управляющего узла двухсетевой архитектуры. Закуплен телекоммуникационный шкаф и оборудование питания для половины вычислительных модулей.
Произведен анализ возможный решений по организации обмена между вычислительными узлами, в результате которого сделан вывод о целесообразности использовании технологии Gigabit Ethernet в связи с более низкой стоимостью и удовлетворительной производительностью. Произведен сравнительный анализ характеристик имеющихся на рынке коммутаторов, выбраны и закуплены два коммутатора: для организации сети управления и поддержки сетевой файловой системы, а также сети обмена данными между вычислительными модулями.
Выполнено комплексное сравнительное тестирование двух узлов различной архитектуры (Pentium-4 и AMD-64), с использованием трех различных компиляторов; обоснован выбор в пользу архитектуры AMD-64 в силу более высокой вычислительной производительности. Приобретен управляющий модуль и 12 вычислительных модулей на процессорах АМD-64.
Рассмотрены технологические решения по охлаждению вычислительной системы. Запланирована организация замкнутого внутреннего воздушного контура охлаждения и внешнего воздушного охлаждения с отводом горячего воздуха за пределы помещения. Приобретен кондиционер для телекоммуникационного шкафа с мощностью охлаждения 4 КВт.
Таким образом, к концу этого года приобретено более половины оборудования, проведены работы по монтажу и установке и начата настройка программного обеспечения для работы кластера МВС-1000/25 во временном, 12-процессорном режиме.
Основные публикации:
- Исаев С. В., Малышев А. В., Шайдуров В. В.
Красноярская сеть параллельных вычислений // Материалы III школы-семинара «Распределенные и кластерные вычисления». — Красноярск: ИВМ СО РАН. — 2004. — С. 67-77.
(Лаборатория вычислительной техники и телекоммуникаций)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н, проф. А. М. Франк
На основе модификации разработанной ранее программы для параллельной ЭВМ проведены расчеты задачи о термокапиллярной конвекции в горизонтальном слое при наличии продольного градиента температуры. Тестовые расчеты показали хорошую сходимость метода для данного класса задач. Сравнение с численными расчетами других авторов позволяет сделать вывод, что для небольших чисел Рейнольдса метод позволяет достаточно точно моделировать процесс с использованием более грубых сеток по пространству для расчета скоростей и температуры.
Основные публикации:
- Frank A. M.
Investigation and suppression of regular structures in a locally heated falling film // Selected Papers of the Inter. conf. «Fluxes and Structures in Fluids». — M.: IPM RAS. — 2004. — P. 70-73.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ
Руководитель:
д.ф.-м.н., проф. Н. В. Еркаев
Разработана магнитогидродинамическая модель нестационарных вариаций магнитного поля и параметров плазмы вблизи границы магнитосферы Земли, связанных с вариациями величины и направления межпланетного магнитного поля в солнечном ветре (Н. В. Еркаев, И. Л. Аршукова).
Определены зависимости скоростей альвеновской и медленной магнитозвуковой волн от кривизны магнитных силовых линий (Н. В. Еркаев, А. В. Шайдуров).
Основные публикации:
- Arshukova I. L., Erkaev N. V., Biernat H. K.
Interchange instability of a curved current layer with smooth monotonic variations of the magnetic field components // Ann. Geophys. — 2004. — Vol. 22. — P. 993–999 .
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. О. В. Капцов
Развивается метод построения редукций и решений гиперболических систем уравнений с частными производными. Он основан на нахождении функций постоянных вдоль характеристик. Примерами таких функций являются инварианты Римана, интеграл Бернулли, инвариант Эртеля. Показано существование функций, постоянных на характеристиках, которые зависят от производных сколь угодно высокого порядка. Дается способ построения таких функций. Наличие большого числа этих функций позволяет редуцировать исходную гиперболическую систему к обыкновенным дифференциальным уравнениям. Данный подход является обобщением метода интегрирования Дарбу уравнений второго порядка с двумя независимыми переменными.
В качестве приложений рассматриваются уравнения газовой динамики и магнитной гидродинамики. Для особых уравнений состояния удается найти широкие классы точных решений, зависящие от произвольных функций.
Основные публикации:
- Капцов О. В.
Инварианты характеристик систем уравнений с частными производными // Сиб. мат. журнал. — 2004. — Т. 45. — № 3. — С. 577–591 . - Капцов О. В.
Системы уравнений с частными производными первого порядка: характеристики и их инварианты // Препринт № 1. — Красноярск: ИВМ СО РАН. — 2004. — 32 с.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. В. М. Садовский
С помощью реологического метода, дополненного новым элементом — жестким контактом, построены феноменологические модели деформирования материалов, по-разному сопротивляющихся растяжению и сжатию. В рамках регуляризованной модели исследованы вопросы разрешимости статических краевых задач при малых деформациях среды. Дано обобщение статической и кинематической теорем теории предельного равновесия. В качестве примера применения этих теорем получена верхняя оценка предельной нагрузки и угла выхода линейной зоны локализации деформаций в задаче о разрыве цилиндрического образца с радиальным надрезом давлением на берегах надреза.
Предложены итерационные по времени процедуры численного решения динамических задач теории упругости для неоднородных сред, позволяющие существенно снизить время счета при наличии в области решения небольших жестких включений.
Выполнен численный анализ ветвления решений в нелинейной краевой задаче выпучивания осесимметричных оболочек-куполов при радиальном сжатии. Построены параметрические диаграммы ветвления, обнаружившие качественно новый характер ветвления по сравнению с соответствующей задачей для пластины: при переходе от пластины к оболочке ветвящиеся диаграммы рвутся на множество изолированных ветвей. Полученные результаты могут быть использованы для предотвращения скачкообразной потери устойчивости куполов.
Основные публикации:
- Богульский И. О., Чеверда В. А.
Итерационная по времени процедура моделирования нестационарных процессов в существенно неоднородных средах // СибЖВМ. — 2004. — Т. 7. — № 4. — С. 283–286 . - Мясников В. П., Садовский В. М.
Вариационные принципы теории предельного равновесия разнопрочных сред // ПММ. — 2004. — Т. 68. — Вып. 3. — С. 488–499 . - Шкутин Л. И.
Численный анализ задачи выпучивания конической оболочки при радиальном сжатии // ПМТФ. — 2004. — Т. 45. — № 5. — С. 151–156 . - Шкутин Л. И.
Численный анализ осесимметричных форм выпучивания пластин при радиальном сжатии // ПМТФ. — 2004. — Т. 45. — № 1. — С. 107–114 .
(Отдел вычислительной механики деформируемых сред)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н. В. В. Денисенко
Усовершенствована численная модель возмущения магнитосферного магнитного поля токами в каспах, которые возникают как следствие пересоединения геомагнитного поля с полем, принесенным солнечным ветром. Использовано решение трехмерной задачи магнитостатики вместо применявшейся ранее аппроксимации пространственно распределенных токов токами на поверхности (В. В. Денисенко).
Найдены характерные времена затухания альвеновских импульсов, многократно отражающихся от ионосферы Земли (Н. В. Еркаев, А. В. Шайдуров).
Основные публикации:
- Денисенко В. В.
Применение энергетических методов при построении векторных полей // Вычислительные технологии. — 2004. — Т. 9. — № 4. — С. 42-56.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ № 902.2003.1 — ведущие научные школы — «Теория и приложения задач со свободной границей»
Руководитель:
чл.-корр. РАН В. В. Пухначев (ИГиЛ СО РАН)
Исполнитель от ИВМ СО РАН:
д.ф.-м.н., проф. В. К. Андреев
Построены новые точные решения вращательно-симметричной модели «глаза» тайфуна. Показано, что в лагранжевых координатах уравнения этой нелинейной модели сводятся к одному линейному дифференциальному уравнению первого порядка (В. К. Андреев, А. А. Родионов).
Проведено исследование устойчивости нестационарного растяжения двуслойной цилиндрической струи идеальной жидкости. Найдено асимптотическое поведение и дано численное решение соответствующих амплитудных уравнений (В. К. Андреев).
Исследованы групповые свойства уравнений термодиффузии в плоском случае. Построены оптимальные системы подалгебр первого и второго порядков для допускаемой алгебры Ли операторов, которая оказалась бесконечномерной. Приведены примеры точных инвариантных решений уравнений термодиффузии. Найдены точные решения, описывающие движение бинарной смеси в наклонном слое со свободной границей, а также в вертикальном слое с твердыми стенками при наличии продольных градиентов температуры и концентрации. Изучено влияние параметра термодиффузии на режим течений (И. И. Рыжков).
Основные публикации:
- Ryzhkov I. I.
Symmetry Analysis and Exact Solutions of the Thermal Diffusion Equations // Abstr. of the 10-th Int. сonf. on Modern Group Analysis. — Larnaca, Cyprus, 2004. — P. 49-50. - Андреев В. К.
Об интегрировании уравнений движения «глаза» тайфуна // Тр. XXXV конф. «Проблемы теоретической и прикладной математики». — Екатеринбург: ИММ УрО РАН. — 2004. — С. 100–104 . - Андреев В. К.
Об устойчивости неустановившегося движения жидкого двуслойного цилиндра // Изв. вузов. Сев.-Кавк. регион. Естеств. науки. — 2004. — Математика и механика сплошной среды. — (Спец. выпуск). — С. 25-28. - Рыжков И. И.
Групповой анализ и точные решения уравнений в плоском случае // Тез. докл. ХХ Всерос. школы-семинара «Аналитические методы и оптимизация процессов в механике жидкости и газа». — Абрау-Дюрсо, 2004. — С. 63-64.
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. В. Н. Лопатин
Подготовлена монография, в которой представлено обобщение исследований закономерностей взаимодействия электромагнитного излучения с оптически мягкими частицами различной формы и структуры для совершенствования схемы решения обратной оптической задачи методами интегральной и «пролетной» индикатрис однократного светорассеяния на основе полученных аналитических связей. Развиты приближенные методы решения прямой оптической задачи и исследованы на их основе закономерности многократного рассеяния лазерного излучения водными биологическими дисперсными средами, в частности, плотной суспензией эритроцитов как модели таких сред, для определения параметров последних. Приведены результаты исследования функциональной структуры природных водных экосистем, полученные на основе разработанных схем дешифрирования оптической информации. Рассмотрены процессы адсорбции растворенных органических веществ на частицах минеральной взвеси и формирования органо-минерального детрита (ОМД), выведены зависимости структурных параметров ОМД от формирующих их факторов, оценена зона влияния граничной поверхности частиц на водную среду. Выявлены внутренние связи и механизмы взаимодействия ОМД с бактерио- и фитопланктоном. Предложена схема включения ОМД в общий комплекс трофической микробиальной петли (В. Н. Лопатин, А. В. Приезжев, А. Д. Апонасенко, Н. В. Шепелевич, В. В. Лопатин, П. В. Пожиленкова, И. В. Простакова).
Основные публикации:
- Методы светорассеяния в анализе водных дисперсных биологических сред / Лопатин В. Н., Приезжев А. В., Апонасенко А. Д., Шепелевич Н. В., Лопатин В. В., Пожиленкова П. В., Простакова И. В.
- М: Физ.-мат. лит., 2004. — 384 с.
(Лаборатория биологической спектрофотометрии)
| К началу | |
Грант РФФИ №
Руководитель:
д.т.н. Л. Ф. Ноженкова
Конгресс проводился с 15 января по 18 января 2004 года. Научная программа конгресса формировалась согласно следующим секциям: математический анализ и дифференциальные уравнения; алгебра, логика и теория чисел; геометрия и топология; вычислительная и прикладная математика, математическое моделирование; информатика, математическое образование. Целью проведения является поддержка молодых ученых-математиков путем привлечения их к участию в конференциях; обеспечение профессионального общения женщин, работающих в теоретической и прикладной математике; методологическая и методическая помощь в научном и образовательном процессе.
Основные публикации:
- Вестник КрасГУ: Сб. тр. III Всесибирского конгресса женщин-математиков. - Красноярск: ИЦ КрасГУ. — 2004. — Вып. 3. -169 с.
- Тез. докл. III Всесибирского конгресса женщин-математиков. - Красноярск: ПФК «ТОРРА». — 2004. -165 с.
Руководитель:
д.ф.-м.н., проф. О. Ю. Воробьев
III Всероссийская конференция по финансово-актуарной математике и смежным вопросам проводилась 27 — 29 февраля 2004 в Институте вычислительного моделирования СО РАН г. Красноярска. В программу конференции были включены 92 доклада 106 участников из 15 городов: Анжеро-Судженск, Барнаул, Владивосток, Гродно (Белоруссия), Златоуст, Екатеринбург, Красноярск, Москва, Новосибирск, Омск, Самара, Санкт-Петербург, Томск, Уфа. К началу конференции был издан сборник тезисов всех представленных докладов. Непосредственно в работе конференции приняло участие 105 человек, из них 29 докторов и кандидатов наук, 76 аспирантов и студентов. Заслушано 4 пленарных и 50 секционных доклада. В рамках конференции состоялись заседания 5 секций: Финансово-актуарная математика (пред. проф. В. Н. Лукин); Эвентология риска и теория случайных событий (пред. проф. О. Ю. Воробьев); Принятие решений в условиях риска и неопределенности (пред. к.ф.-м.н. А. А. Новоселов); Статистические системы природы и общества (пред. проф. Р. Г. Хлебопрос); Математическое моделирование в медицине (пред. проф. В. Ф. Мажаров). Большинство докладов сделаны на высоком научном уровне. Принято решение о проведении IV Всероссийской ФАМ конференции в феврале 2005 года в г. Красноярске.
Основные публикации:
- Тез. докл. III Всерос. конф. по финансово-актуарной математике и смежным вопросам. / Под ред. Д. В. Семеновой. — Красноярск: КрасГУ. — 2004. — 112 с.
- Тр. III Всерос. конф. по финансово-актуарной математике и смежным вопросам. Ч. 1 / Под ред. О. Ю. Воробьёва. — Красноярск: ИВМ СО РАН. — 2003. — 300 с.
- Тр. III Всерос. конф. по финансово-актуарной математике и смежным вопросам. Ч. 2. / Под ред. О. Ю. Воробьёва. — Красноярск: ИВМ СО РАН. — 2004. — 292 с.
| К началу | |
Грант РФФИ №
Руководитель:
чл.-корр. РАН В. В. Шайдуров
Среди многих направлений процесса развития вычислительной техники и расширения области ее применения создание и использование параллельных вычислительных систем — одно из самых перспективных на сегодняшний день.
Школа-семинар состоялась 14-16 сентября 2004 года. В заседаниях школы-семинара на протяжении трех дней участвовало около 100 человек. Произнесено 32 доклада и сообщений с общим числом соавторов 44 человека. В качестве участников были представлены научные сотрудники институтов и преподаватели вузов из Красноярска, Новосибирска, Иркутска, Москвы, Омска, Барнаула, Кишинева. Готовятся к изданию в 2005 году материалы этой школы-семинара.
Принято решение о проведении в 2005 году крупной традиционной международной конференции по параллельному программированию.
Грант РФФИ №Руководитель:
д.ф.-м.н. М. В. Носков (КГТУ)
Исполнитель от ИВМ СО РАН:
к.ф.-м.н. К. В. Симонов
Разработана эффективная вычислительная технология для анализа пространственно-временных данных геомониторинга на основе вейвлет-преобразований. Для увеличения скорости расчета вейвлет-диаграмм применяется распараллеливание алгоритма для многопроцессорных систем. Определены относительные временные затраты на вычисление вейвлет-диаграмм при выделении элементов рельефа заданного размера на основе вейвлет-преобразований модельных данных — космических снимков поверхности Земли. На основе вейвлет-преобразования выполнено моделирование топографических данных с целью выделения кратеров на поверхности Земли (на примере кратеров Логонча и Папигай, расположенных в Красноярском крае).
Основные публикации:
- Носков М. В., Симонов К. В., Перетокин С. А.
Быстрое вейвлет-преобразование сейсмических сигналов // Вычислительные технологии. — 2004. — Т. 9. — (Спец. выпуск). — С. 86-94. - Носков М. В., Симонов К. В., Перетокин С. А.
Быстрое вейвлет-преобразование пространственных данных геомониторинга // Вычислительные технологии. — 2004. — Т. 9. — Вестник КазНУ им. аль-Фараби. Сер. Математика, механика, информатика. — № 3 (42). — (Совм. выпуск. — Ч. 3). — С. 242–245 .
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РГНФ №
Руководитель:
д.т.н., проф. А. В. Лапко
Завершена разработка информационной подсистемы сбора, передачи, хранения и первичной обработки эпидемиологических данных мониторинга артериальной гипертонии с многоуровневой структурой. Создан комплекс программ обнаружения закономерностей распространённости артериальной гипертонии и прогнозирования их показателей по значениям факторов риска. Проведена экспериментальная проверка информационных подсистем сбора, передачи, хранения и первичной обработки данных эпидемиологического мониторинга артериальной гипертонии в реальных условиях ряда районов Красноярского края. На этой основе проведена корректировка математического и программного обеспечения информационных подсистем.
Основные публикации:
- Лапко А. В., Лапко В. А., Гуревич К. Ю., Косов Р. А., Суханов А. В., Якунин Ю. Ю., Ярославцев С. Г.
Непараметрические методы обработки информации в автоматизированной системе мониторинга артериальной гипертонии // Тр. всерос. конф. «Информационно-аналитические системы и технологии в здравоохранении и ОМС». — Красноярск: КМИАЦ. — 2004. — С. 176–184 . - Поликарпов Л. С., Лапко А. В., Хамнагадаев И. И., Яскевич Р. А.
Метеотропные реакции сердечно-сосудистой системы и их профилактика. — Новосибирск: Наука. — 2004. — 194 с.
(Отдел вычислительной математики)
| К началу | |