| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2007 год
Интеграционные, экспедиционные проекты, гранты СО РАН
- Заказные интеграционные проекты
- Междисциплинарные интеграционные проекты
- Комплексные интеграционные проекты
- Экспедиционные проекты
- Целевая программа СО РАН «СуперЭВМ»
- Целевая программа СО РАН «Информационные и телекоммуникационные ресурсы СО РАН»
Комплексные интеграционные проекты
Проект № 2.15 " Построение и анализ новых математических моделей сложных сред"
Организации-исполнители: ИГиЛ СО РАН, ИМ СО РАН, ИВМ СО РАН
Координаторы: ак. РАН Л. В. Овсянников, ак. РАН С. К. Годунов
Исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. В. К. Андреев
1. Изучена задача об устойчивости равновесного состояния слабо сжимаемой жидкости, ограниченной снизу неподвижной твердой, а сверху — теплопроводящей стенкой конечной толщины. Рассмотрена система, состоящая из двух бесконечных слоев Ω1, Ω2 толщиной l1, l2, слой Ω1 занят льдом, а Ω2 заполнен водой. В дальнейшем все величины с индексом «w» относятся к жидкости, заполняющей область z1 < z < z2, а величины с индексом «i» — ко льду, занимающему область 0 < z < z1. В Ω1 справедливо уравнение
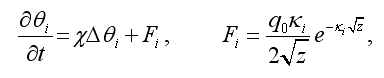
где θ — температура, χ — температуропроводность, Fi — функция теплового источника, q0 — интенсивность теплового потока на поверхности ледяного покрова, κ — показатель поглощения (показатель ослабления солнечной радиации). В Ω2 справедлива система уравнений Обербека-Буссинеска, в которой дополнительно учитывается функция теплового источника FW, описывающая внутреннее тепловыделение
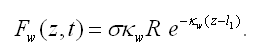
Найдено решение, описывающее состояние механического равновесия и исследуется устойчивость полученного решения по отношению к малым возмущениям. Доказана устойчивость длинноволновых возмущений и численно решена полная спектральная задача. При решении задачи для жидкости использовались значения физических параметров, характерных для воды в озере Байкал. Значения прочих физических параметров (поток тепла, интенсивность теплового потока, толщина льда и др.) принимались равными соответствующим средним значениям для Северного, Центрального и Южного Байкала. На рис. 44 приводятся графики инкрементов нарастания возмущений для различных зон Байкала: 1 — Северный Байкал, критическое волновое число α* = 2.4, критическая длина волны возмущения λ* = 737.91 м; 2 — Южный Байкал, α* = 3.06, λ* = 831.18 м; 3 — Центральный Байкал, α* = 3.26, λ* = 773.44 м.
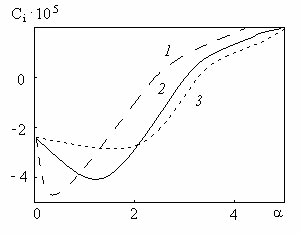
Рис. 44. Инкременты нарастания возмущений
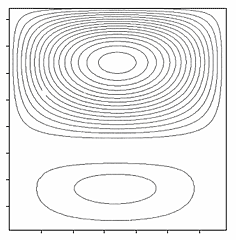
Рис. 45. Линии тока
На рис. 45 приведены линии тока, построенные при значениях параметров, характерных для Центрального Байкала. В отличие от других зон здесь имеются две конвективные ячейки.
Построены нейтральные кривые для различных значений числа Био и найдены критические числа Релея.
Из расчетов следует, что при уменьшении числа Био критические числа Релея убывают, а область неустойчивости смещается в область меньших по значению волновых чисел. Однако рост интенсивности теплообмена имеет слабое стабилизирующее влияние.
2. Исследовано инвариантное решение двумерных уравнений термодиффузионного движения
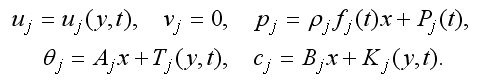
Этому решению можно дать следующую интерпретацию. Предположим, что на границе раздела двух смесей y = 0 поверхностное натяжение линейно зависит от температуры и концентрации: σ(θ, c) = σ0 − κ1θ − κ2c, где κ1 > 0, κ2 — постоянные. В начальный момент времени первая смесь заполняет слой −l1 < y < 0, а вторая — слой 0 < y < l2. Смеси находятся в покое, и при t = 0 во всем пространстве мгновенно создается поле температур θj = Ajx и поле концентраций cj = Bjx. Термоконцентрационный эффект и градиенты давления fj(t) порождают движение смесей, в котором поверхность раздела остается плоскостью y = 0, а траектории являются прямыми, параллельными оси x. Функции uj, Tj, Kj можно назвать возмущениями состояния покоя смесей.
Подстановка вида решения в систему уравнений термодиффузионного движения с учетом условий на границе раздела y = 0 приводит к сопряжённой начально-краевой задаче для функций uj, Tjj, Kj. Доказано, что если интеграл
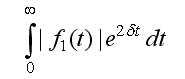
сходится и термоконцентрационные силы отсутствуют на поверхности раздела, то при t → ∞ скорости в слоях по экспоненте стремятся к нулю. То же самое справедливо для температуры и концентрации. Если градиент давления отсутствует, то скорости, температуры и концентрации выходят на стационарный режим: скорости — на течения Куэтта в слоях, а температуры и концентрации описываются полиномами третьего порядка по y. В случае существования конечного предела
скорости выходят на стационарный режим типа течения Пуазейля, а температуры и концентрации описываются полиномами четвёртого порядка по y.
3. Исследована устойчивость конвективного течения в вертикальном слое многокомпонентной жидкости. Данная конфигурация соответствует термодиффузионной колонне (экспериментальная установка для измерения коэффициентов термодиффузии) на начальном этапе разделения смеси. В длинноволновом приближении проведен анализ устойчивости системы в широком диапазоне параметров. Проведены расчеты нейтральных кривых методом пошагового интегрирования с ортогонализацией и описаны механизмы неустойчивости. Предложена математическая модель для анализа относительной устойчивости различных конфигураций.
4. Решена задача групповой классификации системы уравнений конвекции несжимаемой бинарной смеси относительно функции, учитывающей силы плавучести вдоль оси z. Эта функция R(p, T, c) определяет плотность среды, зависит от давления, температуры и концентрации легких компонент в жидкости. Вычислена основная группа преобразований зависимых и независимых переменных системы при произвольном выборе функции, базис ядра состоит из восьми операторов, редуцируемых из системы операторов для уравнений Навье-Стокса. Выделены и рассмотрены три случая: 1) функция R(p, T, c) не зависит от давления p; 2) функция R = p + Φ(T, c) — линейная по p; 3) функция R — нелинейная по p. Получены таблицы групповой классификации со специализациями функции R(p, T, c) и базисами допустимых операторов.
5. Проведена групповая классификация уравнений двумерного нестационарного турбулентного пограничного слоя и найдены некоторые точные решения.
6. Получены решения стационарной и нестационарной задачи о ползущем движении бинарной смеси в горизонтальной цилиндрической трубе. Показано, что нестационарное решение выходит на стационарный режим при больших временах. Найдены решения стационарной задачи при достаточно малых значениях числа Рейнольдса в первом приближении.
Основные публикации:
- Андреев В. К., Картошкина А. Е.
Автомодельное движение бинарных смесей с плоской границей раздела // Сибирский журнал индустриальной математики. — 2007. — Т. 10. — № 1(29). — С. 17-24. - Андреев В. К., Бекежанова В. Б.
Конвективная неустойчивость системы горизонтальных слоёв слабосжимаемых жидкостей // ПМТФ. — 2007. — Т. 48. — № 4. — С. 15-22. - Ефимова М. В.
Неустойчивость поверхности раздела равновесного состояния двух бинарных смесей с учетом эффекта Соре // Вычислительные технологии. — 2007. — Т. 12. — № 6. — С. 18-30. - Андреев В. К.
Свойства решений начально-краевой задачи о совместном движении плоских слоёв вязких жидкостей // Тр. XXXVIII Всерос. конф. «Проблемы теоретичесой и прикладной математики». — Екатеринбург: ИММ УрО РАН. — 2007. — C. 105–110 . - Собачкина Н. Л.
Решение начально-краевой задачи о ползущем движении бинарной смеси в цилиндре // Тр. XXXVIII Всерос. конф. «Проблемы теоретической и прикладной математики». — Екатеринбург: ИММ УрО РАН. — 2007. — С. 199–204 .
(Отдел дифференциальных уравнений механики)
| К началу | |