| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2008 год
Программы РАН
Отделение математических наук
Программа № 1.3 «Современные вычислительные и информационные технологии решения больших задач»
Проект № 1.3.3 «Разработка и исследование вычислительных алгоритмов решения уравнений вязкой несжимаемой жидкости и их применение к задачам гидрофизики»Руководитель: чл.-корр. РАН В. В. Шайдуров
На примере численного решения краевой задачи для уравнений мелкой воды рассмотрены технологические аспекты разработки масштабируемых параллельных алгоритмов для кластерных вычислительных систем с использованием библиотеки MPI.
Для дискретизации уравнений мелкой воды использовался метод конечных элементов с линейными элементами на треугольниках. Для распараллеливания вычислений применялась декомпозиция области с соответствующим разнесением данных по процессорам, причем было рассмотрено два естественных подхода: без перекрытий и с теневыми гранями.
Теоретические оценки показали, что алгоритмы обладают значительным потенциалом параллелизма, что дает ускорение вычислений, близкое к линейному в зависимости от числа процессоров. Причем как с теоретической точки зрения, так и согласно результатам численных экспериментов наиболее эффективной является реализация, основанная на разбиении области без перекрытия подобластей с использованием неблокирующих операций обмена. К тому же, надо отметить как явное преимущество простоту организации параллельного алгоритма при декомпозиции области без перекрытия подобластей на неструктурированных триангуляциях реальных акваторий.
При сравнении реализаций параллельных алгоритмов с помощью MPI и DVM с точки зрения ускорения отмечается некоторое преимущество использования MPI.
Тестовые расчеты для акватории Охотского моря проводились на сетках, подготовленных на основе открытой батиметрической базы данных ЕТОРО2. Численный эксперимент состоял в распространении возмущения, описываемого гауссовской функцией, моделирующей исходное цунами-возмущение. Результаты численного моделирования представлены на рис. 22, где помимо триангуляции изображено возвышение поверхности для некоторых моментов времени (масштаб по вертикали увеличен на три порядка для большей наглядности). Линиями показаны границы, получившиеся при декомпозиции области на 8 частей.
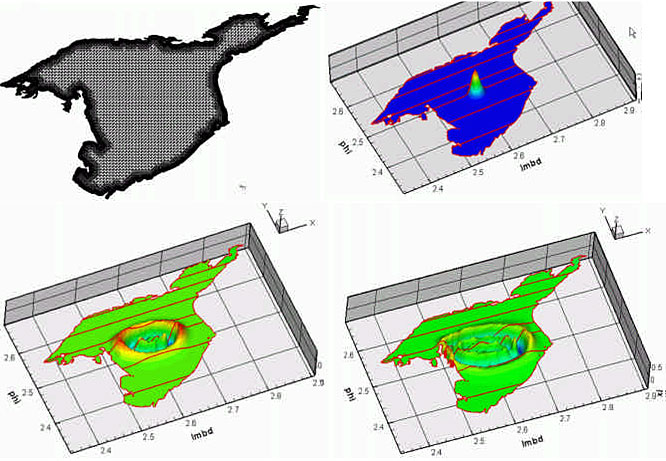
Рис. 22. Численный эксперимент в акватории Охотского моря на 8 процессорах: триангуляция, начальное возмущение, распространение возмущения через 42 и 67 мин
Основные публикации:
- Agoshkov V. I., Kamenschikov L. P., Karepova E. D. and Shaidurov V. V.
Numerical Solution of Some Direct and Inverse Mathematical Problems for Tidal Flows // Notes on Numerical Fluid Mechanics and Multidisciplinary Design. — Berlin: Springer-Verlag. — 2008. — Vol. 101. — P. 41-54. - Каменщиков Л. П., Карепова Е. Д., Шайдуров В. В.
Моделирование распространения крупномасштабных волн в морях и океанах с параллельной реализацией // Тр. IV Сибирской школы-семинара по параллельным и высокопроизводительным вычислениям. — Томск: ТГУ, OOO «Дельтаплан». — 2008. — С. 108–115 .
(Отдел вычислительной математики)
| К началу | |