| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2010 год
Гранты российских научных фондов
- Гранты РФФИ
- Проект РФФИ №
08–01–00 148 — «Параллельные вычисления в задачах динамики упругопластических и сыпучих сред» - Грант РФФИ №
08–01–00 621 — «Вычислительные технологии для расчета течений несжимаемой жидкости» - Грант РФФИ №
08–01–00 762 — «Конвективные течения и их устойчивость в областях с подвижными границами» - Грант РФФИ №
09–01–00 395-а — «Группы с условиями конечности» - Грант РФФИ
08–05–00 258-а — «Исследование механизмов взаимосвязи потоков углекислого газа с физическими, химическими и биологическими процессами в системе «вода-атмосфера» оз. Байкал» - Грант РФФИ №
10–01–00 509-а — «Группы с конечным числом элементов» - Проект РФФИ
10–01–05 016-б — «Развитие МТБ на проведение исследований по области знаний 01 и 07: модернизация и доукомплектование вычислительных ресурсов на основе суперкомпьютера на графических процессорах Tesla» - Грант РФФИ №
09–05–91 000-АНФ-а — «МГД аспекты «флэппинг» колебаний токового слоя магнитосферного хвост» - Грант РФФИ №
10–01–06 003-г — «Организация и проведение VI Всесибирского конгресса женщин-математиков» - Грант РФФИ №
10–01–06 089-г — «Организация и проведение XIII Всероссийского семинара «Моделирование неравновесных систем» - Проект РФФИ №
10–01–06 826-моб_г — «Организация и проведение Седьмой межрегиональной школы-семинара «Распределенные и кластерные вычисления» - Проект РФФИ №
10–01–08 059-з — «Участие в IV Европейской конференции по вычислительной механике» - Грант РФФИ
10–07–09 242-моб_з — «Участие в международной конференции по информатике (ICCS 2010)» - Гранты Президента РФ
- Гранты Красноярского краевого фонда поддержки науки и научно-технической деятельности
Гранты РФФИ
Проект РФФИ №
Руководитель: д.ф.-м.н., проф. В. М. Садовский
Получено обобщение математической модели моментного континуума Коссера, в которой наряду с поступательными степенями свободы учитывается вращение частиц микроструктуры материала, на случай конечных деформаций и поворотов частиц. Соответствующая система уравнений приведена к самосогласованной системе законов сохранения. С ее помощью получена симметрическая форма записи уравнений, гарантирующая гиперболичность и позволяющая применить к исследованию краевых задач эффективные численные методы — различные модификации метода распада разрыва Годунова. На ее основе получен общий вид начальных и граничных условий, корректных по Адамару. Разработаны эффективные алгоритмы для численного исследования модели на многопроцессорных вычислительных системах.
Как частный случай, в предположении о зависимости потенциала напряжений только от двух инвариантов — объемной деформации среды и относительного угла поворота частицы, на основе этой модели получена система уравнений, описывающая термомеханическое состояние нематического жидкого кристалла при слабых силовых и температурных воздействиях. В плоском случае линеаризованная система, записанная в скоростях и напряжениях, сводится к шести уравнениям — трем уравнениям поступательного и вращательного движения, уравнениям для давления и для касательного напряжения, вызванного вращением частиц, и связанного уравнения теплопроводности. Путем дифференцирования из системы получено уравнение Клейна-Гордона для касательного напряжения. Это уравнение характеризует основное отличие жидкого кристалла от обычной акустической среды, связанное с наличием резонанса на частоте собственных колебаний вращательного движения частиц.
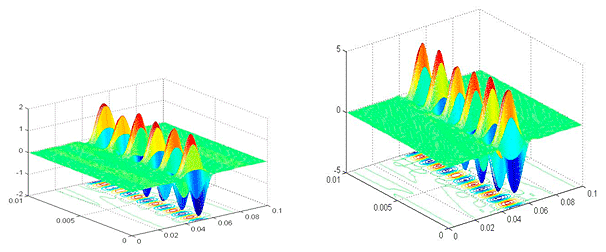
Рис. VI.1. Возбуждение резонанса на частоте собственных колебаний вращательного движения частиц (с 500-го по 1000-й шаг по времени амплитуда безразмерного давления увеличивается практически вдвое)
Построена разностная схема типа Неймана-Рихтмайера второго порядка точности для численного исследования динамики жидкокристаллической среды под действием механических напряжений. Разработан вычислительный алгоритм и компьютерная программа в среде Matlab. Выполнены расчеты резонансного возбуждения движения частиц (линейных молекул жидкого кристалла) на частоте собственных колебаний вращательного движения за счет периодического локализованного воздействия касательными усилиями на границе среды (рис. VI.1). В серии расчетов показано, что резонанс на данной частоте не связан с размерами области решения задачи.
Основные публикации:
- Sadovskaya O. V., Sadovskii V. M.
Numerical Analysis of the Waves Propagation Processes in Elastic-Plastic and Granular Media on Multiprocessor Computer Systems // Zbornik radova konferencije MIT 2009. Kosovska Mitrovica: Prirodno-matematicki fakultet; Novosibirsk: Institute of Computational Technologies SB RAS. — 2010. — P. 358–361 . - Varygina M. P., Sadovskii V. M.
Parallel Computations in the Problems of Dynamics of the Cosserat Continuum // Zbornik radova konferencije MIT 2009. Kosovska Mitrovica: Prirodno-matematicki fakultet; Novosibirsk: Institute of Computational Technologies SB RAS. — 2010. — P. 422–425 . - Sadovskaya O. V., Sadovskii V. M.
Analysis of Rotational Motion of Material Microstructure Particles by Equations of the Cosserat Elasticity Theory // Acoustical Physics. — V. 56. — № 6. — P. 942–950 .
(Отдел вычислительной механики деформируемых сред)
| К началу | |
Грант РФФИ №
Руководитель: член-корреспондент РАН В. В. Шайдуров
1. Предложен, исследован и применен в нескольких задачах фрактальный алгоритм построения последовательности неравномерных вложенных двумерных триангуляций по известной характеристической функции двумерной области. В основе рассматриваемого метода триангуляции лежит единственность представления прямоугольного равнобедренного треугольника в виде объединения двух подобных треугольников (рис. VI.2). На базе этого метода триангуляции разработан алгоритм построения последовательности неравномерных вложенных сеток по известной характеристической функции двумерной области и в соответствии с заданной на области функцией локального размера триангуляции (рис. VI.3).
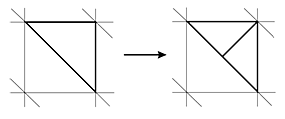
Рис VI.2. Шаблон для разбиения прямоугольного треугольника
Оказалось, что предложенный метод является не описанной в литературе модификацией метода бисекции, когда в каждом из треугольников сетки выделяется только одна вершина, из которой разрешается проводить медиану. Представление элемента триангуляции в виде объединения ему подобных встречается во фрактальной геометрии при построении широко известной «салфетки» Серпинского. Поэтому употребление термина «фрактальный» в названии рассматриваемого алгоритма триангуляции является естественным.
Фрактальный алгоритм триангуляции области приводит к естественному упорядочиванию узлов сетки, что позволяет построить процедуру, обратную процедуре построения сетки (рис. VI.4). Процесс объединения может играть существенную роль в уменьшении временных затрат на решение систем линейных алгебраических уравнений (СЛАУ) в методе конечных элементов, построенных на базе фрактальной триангуляции. Например, в методе Гаусса для решения СЛАУ в качестве ведущих элементов глобальной матрицы жёсткости можно брать её диагональные элементы в порядке, обратном порядку появления узлов сетки в процессе её построения по предлагаемому алгоритму.
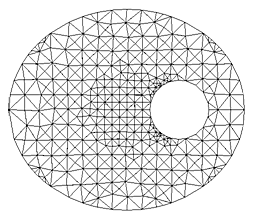
Рис. VI.3. Пример работы алгоритма
Проведённые вычислительные эксперименты показали, что по точности результаты незначительно отличаются от решения СЛАУ методом Гаусса с выбором максимального элемента по столбцу, однако полученная в ходе процесса исключения матрица является более разреженной, чем аналогичная матрица из метода Гаусса. Кроме того, вложенность сеток позволяет реализовать метод Холецкого решения СЛАУ без предварительного формирования глобальной матрицы, проводя исключения искомых узловых значений из локальных матриц жёсткости.
2. В отчетный период продолжались исследования, связанные с решением задачи на ассимиляцию данных наблюдений для моделей мелкой воды в больших акваториях.
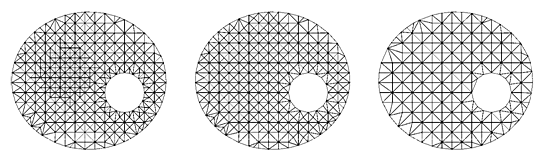
Рис. VI.4. Процесс объединения треугольников сетки.
Прямая задача ставится в области произвольной формы с достаточно гладкой границей, заданной на геосфере. Граница области состоит из «твердых» участков — береговой линии и «жидких» участков — условной границы по воде. На части «жидкой» границы известны данные наблюдений за возвышением свободной поверхности.
В общем случае граничные условия на «жидкой» границе содержат граничную функцию, которую следует найти вместе с неизвестными задачи — скоростями и возвышением свободной поверхности. В области поставлена задача на ассимиляцию данных наблюдений, для решения которой используются методы оптимизации и теории управления.
Рассмотрено два семейства задач оптимального управления с регуляризацией для отыскания минимума нормы разности между искомым и наблюденным возвышениями свободной поверхности. Построен итерационный численный метод восстановления граничной функции в качестве решения обратной задачи в области. Метод состоит в итерационном уточнении граничной функции путем численного решения последовательности прямых и сопряженных задач.
Численное решение прямых и сопряженных задач основано на методе конечных элементов, для чего реализовано, оттестировано и исследовано на эффективность параллельное ПО с использованием технологии MPI. Полученная параллельная программа обладает хорошей масштабируемостью на достаточно большом диапазоне процессоров с эффективностью распараллеливания 0.85.
Продемонстрировано восстановление решения для тестовых задач в акватории Охотского моря для «данных наблюдений», задаваемых: гладкой функцией; функцией, возмущенной белым шумом; функцией с отсутствующими наблюдениями на части жидкой границы.
Начаты также работы по поиску оптимального алгоритма для распараллеливания с помощью технологии OpenMP. Проблема заключается в том, что реализованный алгоритм имеет существенную зависимость по данным в основных циклах, что препятствует непосредственному оптимальному распараллеливанию. Ведется поиск алгоритма, допускающего декомпозицию процесса на достаточно независимые по памяти нити.
3. Построен метод второго порядка точности для решения жестких аддитивных задач. Получены неравенства для контроля точности вычислений и оценка ошибки. По результатам расчетов задач химической кинетики следует значительное повышение эффективности по сравнению с известными методами. Построен аддитивный метод третьего порядка точности для решения жестких неавтономных задач. Получены неравенства для контроля точности вычислений и устойчивости численной схемы. Работоспособность и эффективность метода исследована на примере моделирования кольцевого модулятора (рис. VI.5).
Рис. VI.5. Кольцевой модулятор
Оба метода ориентированы на численное решение задач механики сплошной среды, в которых после дискретизации по пространству методом конечных элементов или с помощью конечных разностей возникает начальная задача для жесткой аддитивной неавтономной системы обыкновенных дифференциальных уравнений. При реализации численных формул необходимо два раза в методе второго порядка и четыре раза в методе третьего порядка точности решать линейную систему алгебраических уравнений. В задачах механики сплошной среды эффективность алгоритма интегрирования может быть достигнута за счет специальных методов решения линейных систем с симметричной матрицей, которая во многих случаях положительно определена. Данные методы можно применять для решения локально-неустойчивых задач. В отличие от A-устойчивых или L-устойчивых методов, у которых область неустойчивости обычно небольшая и которые являются A-устойчивыми или L-устойчивыми не только в левой, но и в правой полуплоскости плоскости, построенные методы являются неустойчивыми практически во всей правой полуплоскости и поэтому более предпочтительны при определении неустойчивого решения.
Разработан параллельный вариант явного метода типа Рунге-Кутты второго порядка точности. Предложенная параллельная вычислительная схема метода ориентирована на многопроцессорные вычислительные системы кластерной архитектуры.
Построена параллельная вычислительная схема аддитивного метода второго порядка, ориентированная на применение в многопроцессорных вычислительных системах кластерной архитектуры с применением топологии «полный граф» и «гиперкуб». Основной подход при формировании параллельного алгоритма метода состоит в использовании декомпозиции на подзадачи и установлении взаимосвязи между ними. Проведены тестовые расчеты.
4. Известные оценки сходимости для многосеточных методов получены в предположении, что элементы матрицы жесткости и вектора правой части системы уравнений метода конечных элементов вычислены точно. Однако на практике для их вычисления, как правило, используют квадратурные формулы. Это вносит дополнительную погрешность в результат. Для двух версий многосеточного метода (полного многосеточного алгоритма на основе W-цикла и каскадного алгоритма) получены оценки сходимости с учетом численного интегрирования. При этом для построения систем уравнений на последовательности сеток использован подход, позволяющий вычислять элементы матрицы на более крупной сетке через элементы матрицы на более мелкой сетке с помощью операторов интерполяции и проектирования. Обоснована оптимальная вычислительная сложность обоих многосеточных алгоритмов.
5. Исследована новая модель неустановившегося движения водных масс, развивающая методы математического моделирования для целей гидрологических прогнозов. Модель основана на статистической теории турбулентности, методах оптимизации для ассимиляции детальных данных наблюдений в нижних бьефах ГЭС.
Предлагаемый подход основан на использовании для оптимизации моделей имеющихся в распоряжении гидрометслужбы данных наблюдений и позволяет отказаться от многих, как правило, неизвестных параметров в традиционных (типа Сен-Венана) моделях нестационарного распространения воды в русле (сечений русла, коэффициентов шероховатости, начальных данных по длине русла и др.).
Численная реализация модели проводится в среде MathLab с элементами программирования на языке C++ и использованием параллельного программного обеспечения Parallel Computing Toolbox.
Основные публикации:
- Новиков Е. А.
Численное моделирование модифицированного орегонатора (2,1)-методом решения жестких задач // Вычислительные методы и программирование: новые вычислительные технологии. — 2010. — Т. 11. — С. 281–288 . - Новиков Е. А.
Аддитивный метод второго порядка для решения жестких задач // Системы управления и информационные технологии. — 2010. — № 2. — С. 17-21. - Ващенко Г. В., Новиков Е. А.
Параллельный алгоритм (2,1)-метода решения жестких задач // Естественные и технические науки. — 2009. — № 6. — С. 550–554 . - Новиков Е. А., Ващенко Г. В.
Параллельная столбцовая схема и алгоритм (2,1)-метода решения жестких задач // Вестник ИжГТУ. — 2010. — № 1(40). — С. 150–153 . - Ващенко Г.В, Новиков Е. А.
Параллельная реализация явных методов типа Рунге-Кутты // Вестник КрасГАУ. — 2010. — № 2. — С.14-18. - Новиков A. E., Новиков E. A.
Численное решение жестких задач с небольшой точностью // Математическое моделирование. — 2010. — Т. 22. — № 1. — С.46-56. - Novikov A. E., Novikov E. A.
Numerical Integration of Stiff Systems with Low Accuracy // Mathematical Models and Computer Simulations. — 2010. — Vol. 2. — № 4. — P. 443–452 . - Новиков А. Е., Новиков Е. А., Шорников Ю. В., Достовалов Д. Н.
Численное моделирование гибридных систем явным методом третьего порядка в инструментальной среде ИСМА // Проблемы информатики. — Новосибирск: НГТУ. — 2010. — №3 (7). — С. 73-80. - Новиков Е. А.
Аддитивный метод третьего порядка для решения жестких неавтономных задач // Сибирский журнал индустриальной математики. — 2010. — Т. 13. — № 1. — С. 84-94. - Дементьева Е. В., Карепова Е. Д.
Анализ параллельных реализаций МКЭ для моделей мелкой воды // V Сибирская конф. по параллельным и высокопроизводительным вычислениям. — Томск: Том. ун-т. — 2010. — С. 87-91. - Karepova E., Shaidurov V., Dementyeva E.
Parallel Implementation of Numerical Solution for Some Direct and Inverse Mathematical problems for Tidal Flows // 5th Int. Conf. «Inverse Problems: Modeling and Simulation» (IP:M&S). — Turkey, Izmir: Izmir University Publ.. — 2010. — P. 78-79. - Karepova E., Shaidurov V.
Numerical solution of assimilation data problem for tidal flows // 5th Int. Conf. on Finite Difference Methods: Theory and Applications. — Bolgaria, Rousse: University of Rousse Publ. — 2010. — P. 12-13. - Karepova E., Dementyeva E., Malyshev A.
Some effectiveness aspects of finite element method for problem of approximate hydrodynamics on cluster systems // 5th Int. Conf. on Finite Difference Methods: Theory and Applications. — Bolgaria, Rousse: University of Rousse Publ. — 2010. — P. 12. - Дементьева Е. В., Карепова Е. Д., Малышев А. В.
Сравнение реализаций MPI: управление памятью, обмены данными в SMP-узловых кластерах // Материалы междунар. науч.-техн. конф. «Суперкомпьютерные технологии: разработка, программирование, применение (СКТ-2010)». — Таганрог: ТТИ ЮФУ. — Т. 1. — 2010. — С.68-72. - Novikov E. A., Vashchenko G. V.
Explicit Runge-Kutta method 2nd order: parallel algorithm on accuracy and stability control // First Russia and Pacific Conf. on Computer Technology and Applications, Vladivostok, Russia. — 2010. — Р. 202–204 . - Новиков Е. А.
Явные методы Рунге-Кутта: алгоритмы с контролем точности вычислений // Вестник ТюмГУ. — № 6. — (принята к печати).
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., проф. В. К. Андреев
1. Изучено инвариантное решение задачи о совместном движении бинарной смеси и вязкой теплопроводной жидкости в теплоизолированной цилиндрической трубе. Движение происходит под действием продольного градиента давления в смеси. Вязкая жидкость (смазка) и смесь не смешиваются и имеют общую поверхность раздела. Задача сводится к сопряженной начально-краевой задаче для параболических уравнений. Найдено стационарное решение задачи, в котором поля скоростей являются такими же, как у течения Пуайзеля, а температура и концентрация являются полиномами четвертого порядка по радиальной координате. Нестационарная задача решена методом преобразования Лапласа. Численные расчеты показывают, что решение этой задачи сходится к стационарному распределению при t → &inf;, если градиент давления стабилизируется по времени на бесконечности.
2. Исследовано совместное однонаправленное движение трех вязких жидкостей под действием градиента давления в слое, ограниченном твердыми стенками. Анализ движения сводится к решению сопряженной начально-краевой задачи для трех параболических уравнений. Найдено точное стационарное решение поставленной задачи. Решение нестационарной задачи получено методом преобразований Лапласа в виде конечных аналитических формул. Доказано, что если градиент давления в одной из жидкостей имеет конечный предел при t → &inf;, то и решение выходит на стационарный режим. Численное обращение преобразования Лапласа позволяет найти решение при любом заданном градиенте давления.
3. Термокапиллярный эффект существенно влияет на процесс роста кристаллов методом зонной плавки. Для изучения процессов в зоне расплава часто используется модель жидкого моста (или половинной зоны). В данной модели объем жидкости помещен между двумя цилиндрическими стержнями, которые имеют общую ось и расположены на некотором расстоянии друг от друга. Разность температур между стержнями приводит к возникновению градиента поверхностного натяжения на свободной границе, который, в свою очередь, вызывает термокапиллярное движение жидкости. При небольших разностях температур термокапиллярное течение стационарное, однако с ростом разности температур это течение может стать неустойчивым. Развитие неустойчивости связано с появлением монотонных или колебательных возмущений, при этом последние представляют собой стоячие или бегущие гидротепловые волны (характеризуемые азимутальным волновым числом m). Аналогичная неустойчивость в зоне расплава приводит к ухудшению качества кристалла в процессе роста методом зонной плавки.
Устойчивость стационарного термокапиллярного течения в бесконечном жидком мосте была изучена в работе [Xu & Davis, Phys. Fluids, 27, 1102, 1984]. Были определены критические числа Марангони для мод m = 0 и m = 1. Показано, что критическое число Марангони растет с увеличением числа Прандтля. При Pr < Pr* критической модой является m = 1, в то время как для Pr > Pr* критическая мода есть m = 0. Значение Pr* зависит от числа Био. Данные результаты в теории жидких мостов хорошо известны и часто цитируются в литературе.
В рамках проекта линейный анализ устойчивости стационарного течения в жидком мосте существенно пересмотрен [1, 2]. Результаты предыдущих исследований для моды m = 1 подтверждены в области малых чисел Прандтля. В то же время показано, что для больших чисел Прандтля граница устойчивости в плоскости (Pr, Ma) лежит ниже, чем это было установлено ранее. Обнаружено, что нейтральные кривые в плоскости (k, Ma) имеют два локальных минимума (здесь k — осевое волновое число). Один из этих минимумов был известен ранее, однако глобальный минимум определен в данной работе впервые. Полученные результаты гораздо лучше согласуются с экспериментом, чем данные работы [Xu & Davis, Phys. Fluids, 27, 1102, 1984]. В отличие от последней, было показано, что мода m = 1 всегда является критической. Таким образом, смена критической моды с m = 1 на m = 0 с ростом числа Прандтля не происходит.
4. Построено инвариантное решение уравнений термодиффузии с учетом нелинейной зависимости силы плавучести от температуры и концентрации. Оно является вращательно-симметричным и описывает восходящие вихревые течения, переносящие примесь от дна глубоких водоемов к поверхности. Вектор скорости имеет все три не нулевые компоненты в цилиндрической системе координат. Анализ такого стационарного течения сводится к исследованию краевой задачи для нелинейной системы обыкновенных дифференциальных уравнений, которая имеет, в зависимости от физических параметров, неединственное решение. Даны оценки количества примеси, привносящейся на поверхность водоема.
5. Рассмотрено совместное стационарное однонаправленное течение двух несмешивающихся вязких жидкостей в плоском слое при отсутствии силы тяжести. Система ограничена твердыми стенками, на которых задана температура, линейно зависящая от продольной координаты. Одна из стенок неподвижна, а вторая может двигаться с постоянной скоростью. Вдоль поверхности раздела действуют касательные силы, причем поверхностное натяжение линейно зависит от температуры. В качестве дополнительного условия задан расход жидкости m1 в первом слое.
Построено точное решение, описывающее течение в системе при совместном действии термокапиллярных сил, градиентов давления и движении стенки. Получено несколько условий, при которых реализуются течения определенного вида:
- условие на скорость движения стенки, при котором можно добиться нулевого объемного расхода во втором слое;
- условие на градиент температуры, так, чтобы в слоях отсутствовал градиент давления;
- условия, при которых во втором слое наблюдается состояние покоя.
Исследована устойчивость двухслойного течения для системы азот (первая жидкость) — FC-72 (вторая жидкость) в случае 3. На основе численных расчетов показано, что длинноволновые возмущения всегда затухают. Определены критические длины волн, при которых состояние системы с покоящимся вторым слоем становится неустойчивым. Имеет место смена режимов неустойчивости в зависимости от величины градиента температуры на стенках канала. При небольших градиентах температур на стенках все возмущения являются монотонными. С ростом градиента температуры меняется характер неустойчивости и появляются колебательные возмущения, которые имеют ячеистую структуру и сносятся в направлении течения первого слоя.
Основные публикации:
- Бекежанова В. Б.
Конвективная неустойчивость течения Марангони-Пуазейля при наличии продольного градиента температуры // ПМТФ. — 2011 (в печати). - Андреев В. К., Степанова И. В.
Симметрия уравнений термодиффузии при нелинейной зависимости силы плавучести от температуры и концентрации // Вычислительные технологии. — 2010. — Т. 15. — № 4. — С. 47-56. - Ефимова М. В.
Монотонные возмущения равновесного состояния двухслойной системы бинарных смесей // J. of Siberian Federal University. Mathematics and Physics. — 2010. — № 3(4). — С. 507–514 . - Рыжков И. И.
О термокапиллярной неустойчивости в жидком мосте // Тез. докл. XI Всерос. конф. молодых ученых по математическому моделированию и информационным технологиям. — Новосибирск. — 2010. — С. 36-37. - Ryzhkov I. I.
Thermocapillary instabilities in liquid bridges revisited // J. Physics of Fluids. — 2010 (направлена в печать). - Рыжков И. И.
Неустойчивость Рэлея-Бенара в многокомпонентной смеси с эффектом Соре // Тезисы докладов XI Всероссийской школы-конференции молодых ученых «Актуальные вопросы теплофизики и физической гидрогазодинамики». — Новосибирск. — 2010. — C.
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., проф. В. П. Шунков
Доказана теорема, дающая новый признак непростоты для класса групп Шункова. Установлены и доказаны свойства почти слойно конечных групп. Получена характеризация группы Шункова с сильно вложенной почти слойно конечной подгруппой.
Изучались бесконечные группы с условием почти слойной конечности нормализаторов конечных нетривиальных подгрупп. Установлено строение бесконечных силовских 2-подгрупп в группах Шункова с таким условием.
Достроены алгебраические и частично компьютерные модели F-многогранников. Выпуклый правильногранник называется F-многогранником, если при соединении с любым выпуклым правильногранником он перестаёт быть выпуклым правильногранником. Построены все соединения тетраэдров и правильногранных пирамид, являющихся m-правильногранниками при m = 0,1. Создана нулевая версия электронного атласа выпуклых правильногранников. Найдены новые мазуровские тройки знакопеременных групп 14-й и 15-й степени.
Частично классифицированы составные 0-правильногранники. В основном завершен анализ доказательства теоремы Иванова-Пряхина о полноте известного списка несоставных тел для получения более общей и с более прозрачным доказательством теоремы о классификации несоставных 0-,1-правильногранников. Найдены новые мазуровкие тройки знакопеременных групп А{14} и A{15}. Построены гамильтоновы циклы в соответствующих графах Кэли.
Для ряда групп Шевалле малых рангов над полями небольших порядков получено точное значение или достаточная оценка для числа орбит при действии некоторой силовской 2-подгруппы сопряжениями на множестве сопряженных силовских 2-подгрупп, тривиально пересекающейся с ней.
Основные публикации:
- Сенашов В. И.
О группах Шункова с сильно вложенной почти слойно конечной подгруппой // Труды ИММ УрО РАН. — 2010. — Т. 16. — № 3. — С. 234–239 . - Сенашов В. И.
О строении силовских подгрупп в некоторых группах Шункова и о почти слойно конечных группах // Тр. междунар. алгебраической конф. «Алгебра и ее приложения». — Нальчик: Каб.-Балк. ун-т. — 2010. — С. 149–153 . - Сенашов В. И.
О строении силовских подгрупп в некоторых группах Шункова // Тез. докл. междунар. конф. «Алгебра, логика и приложения». — Красноярск: СФУ. — 2010. — С. 79-80. - Senashov V. I.
On Shunkov groups with a strongly embedded subgroup // Proceedings of the Steklov Institute of Mathematics. — 2009. — Vol. 266. — № 12. — P. 210–217 . - Павлюк И. И., Унгер Н. В., Шунков В. П.
О сопряжении подмножеств в группе // Науч. журнал. Вестник ПГУ. Физ.-мат. серия. — 2010. — № 3-4. — P. 66-79. - Павлюк И. И., Шунков В. П.
О группах с ограничениями на коммутаторные классы сопряженных элементов // Тез. докл. междунар. конф. «Алгебра, логика и приложения». — Красноярск: СФУ. — 2010. — С. 72-73. - Зенков В. И., Макосий А. И.
О пересечениях силовских 2-подгрупп в группе Aut(L_4(9)) // Тез. докл. междунар. конф. «Алгебра, логика и приложения». — Красноярск: СФУ. — 2010. — С. 41-42. - Зенков В. И., Макосий А. И.
О пересечениях силовских 2-подгрупп в конечных группах, I // Владикавказский матем. журнал. — 2009. — Т. 11. — № 4. — С. 16-21. - Зенков В. И., Макосий А. И.
О пересечениях силовских 2-подгрупп в группах автоморфизмов групп лиева типа над полем порядка 9 // Тез. докл. междунар. конф. «Мальцевские чтения». — Новосибирск: ИМ СО РАН. — 2010. — С. 68.
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ
Руководитель: к.г.н. В. М. Домышева (Лимнологический институт СО РАН)
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. В. В. Заворуев
Выявлено снижение рН до минимальных значений к 6 — 9 часам дня и возрастание до максимальных значений к 15 или 18 часам дня. Данная зависимость прослеживается во все годы и во все сезоны. При этом суточный ход Fвар (коэффициента фотосинтетической активности), как правило, противоположен ходу рН.
Основные публикации:
- Заворуев В. В., Домышева В. М., Сакирко М. В., Панченко М. В., Пестунов Д. А.
Оценка межгодовой изменчивости содержания углекислого газа в поверхностной воде оз. Байкал // Материалы междунар. конф. «Ресурсная экономика, изменение климата и рациональное природопользование». — Красноярск: ИПК СФУ. — 2009. — С. 761–769 . - Заворуев В. В., Панченко М. В., Домышева В. М., Сакирко М. В., Пестунов Д. А.
Суточный ход вариабельной флуоресценции фитопланктона озера Байкал // Тез. докл. V Верещагинской Байкальской конф. — Иркутск: ОАО, «Иркутская областная типография № 1". — 2010. — С. 205–206 .
(Отдел вычислительной физики)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., проф. А. И. Созутов (СФУ)
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. В. И. Сенашов
Установлены свойства почти слойно конечных групп и на основе этих свойств охарактеризованы группы Шункова с сильно вложенной почти слойно конечной подгруппой.
Изучались бесконечные группы с условием почти слойной конечности нормализаторов конечных нетривиальных подгрупп. Установлено строение бесконечных силовских 2-подгрупп в некоторых группах Шункова.
Основные публикации:
- Сенашов В. И.
О группах Шункова с сильно вложенной почти слойно конечной подгруппой // Труды ИММ УрО РАН. — 2010. — Т. 16. — № 3. — С. 234–239 . - Сенашов В. И.
О строении силовских подгрупп в некоторых группах Шункова и о почти слойно конечных группах // Тр. междунар. алгебраической конф. «Алгебра и ее приложения». — Нальчик: Каб.-Балк. ун-т. — 2010. — С. 149–153 . - Сенашов В. И.
О строении силовских подгрупп в некоторых группах Шункова // Тез. докл. междунар. конф. «Алгебра, логика и приложения». — Красноярск: СФУ. — 2010. — С. 79-80. - Senashov V. I.
On Shunkov groups with a strongly embedded subgroup // Proceedings of the Steklov Institute of Mathematics. — 2009. — Vol. 266. — № 12. — P. 210–217 . - Павлюк И. И., Шунков В. П.
О группах с ограничениями на коммутаторные классы сопряженных элементов // Тез. докл. междунар. конф. «Алгебра, логика и приложения». — Красноярск: СФУ. — 2010. — С. 72-73.
(Отдел дифференциальных уравнений механики)
| К началу | |
Проект РФФИ
Руководитель: член-корреспондент РАН В. В. Шайдуров
Финансовые средства данного проекта направлены на приобретение мощного суперкомпьютера на графических ускорителях Tesla и сервера, необходимого для его подключения к глобальной сети, в интересах обеспечения и развития фундаментальных исследований, проводимых ИВМ СО РАН, институтами Красноярского научного центра Сибирского отделения РАН и расположенными на территории Красноярского края научными и образовательными учреждениями.
В настоящее время в ИВМ СО РАН продолжается финансирование 11 проектов РФФИ, в рамках которых используются информационно-телекоммуникационные ресурсы, параллельные вычисления, суперкомпьютерные и грид-технологии:
Кроме того, на вычислительной базе ИВМ СО РАН выполняется ряд проектов РФФИ от СФУ, Института физики им. Л. В. Киренского СО РАН и Института биофизики СО РАН.
Являясь головным институтом Красноярского научного центра в сфере супервычислений, ИВМ СО РАН планирует дальнейшее наращивание вычислительных мощностей для обеспечения собственных потребностей и потребностей научных коллективов сторонних организаций. Приобретение современного суперкомпьютера на графических процессорах — очередной этап этого процесса.
(Отделы Вычислительной математики, Вычислительной механики деформируемых сред, Служба средств телекоммуникаций и вычислительной техники)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., проф. Н. В. Еркаев
Разработана трехмерная магнитогидродинамическая модель «флэппинг» колебаний и неустойчивости токового слоя магнитосферного хвоста с учетом сжимаемости и эффектов Холла. На основе численных экспериментов найдены дисперсионные зависимости собственных частот от волнового числа для симметричных и изгибных мод колебаний. Результаты численного моделирования удовлетворительно согласуются с экспериментом.
Основные публикации:
- Erkaev N. V., Semenov V. S., Biernat H. K.
Hall magnetohydrodynamic effects for current sheet flapping oscillations related to the magnetic double gradient mechanism // Physics of Plasmas. — V. 17. — P. 60703. - Amerstorfer U., Erkaev N. V., Taubenschuss U., Biernat H. K.
Influence of a density increase on the evolution of the Kelvin-Helmholtz instability and vortices // Physics of Plasmas. — V. 7. — P. 072901-8. - Farrugia C. J., Erkaev N. V., Torbert R. B., Biernat H. K., Gratton F. T., Szabo A., Lin R. P., Ogilvie K. W., Lepping R. P., Smith S. W.
Magnetosheath for almost-aligned solar wind magnetic field and flow vectors: Wind observations across the dawnside magnetosheath at X = -12 Re // J. Geophys. Res.. — V. 115. — № 7. — P. A08227. - Taubenschuss U., Erkaev N. V., Biernat H. K., Farrugia C. J., Mostl C., Amerstorfer U. V.
The role of magnetic handedness in magnetic cloud propagation // Annales Geophysicae. — V. 28. — P. 1075–110 0. - Rubab N., Erkaev N. V., Langmayr D., Biernat H. K.
Kinetic Alfven wave instability in a Lorentzian dusty magnetoplasma // Physics of Plasmas. — V. 17. — P. 103704. - Korovinskiy D., Ivanova V., Biernat H., Erkaev N., Semenov V.
Double gradient instability in a compressible plasma current sheet // Int. Сonf. «Problems of Geocosmos». — St.-Petersburg. — 2010. — С. 132–136 . - Korovinskiy D., Biernat H.; Semenov V.; Erkaev N.; Divin A.
2.5D EHMHD analytical model of steady-state Hall magnetic reconnection in a compressible plasma // Int. Сonf. «Problems of Geocosmos». — St.-Petersburg. — 2010. — С. 126–131 . - Еркаев N. V., Семенов B. C., Рабецкая О. И., Мезенцев А. В., Бирнат Х. К.
Холловская МГД модель «Флэппинг» колебаний токового слоя магнитосферного хвоста // Сб. тез. докл. V Междунар. конф. «Солнечно-земные связи и физика предвестников землетрясений». — Паратунка, Камчатский край. — 2010. — С. 4.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., проф. Л. Ф. Ноженкова
15-17 января 2010 года при поддержке Российского фонда фундаментальных исследований и Сибирского федерального университета проведена Всероссийская конференция «VI Всесибирский конгресс женщин-математиков», приуроченная ко дню рождения выдающегося русского математика Софьи Васильевны Ковалевской. Основная цель Конгресса — расширить профессиональное общение ученых, работающих в теоретической и прикладной математике и информатике, повысить научную квалификацию и обеспечить обмен опытом учителей математики и информатики общеобразовательных школ, преподавателей вузов, поддержать деятельность молодых ученых и специалистов. Научная программа конференции включала пленарные и секционные заседания по следующим направлениям: математический анализ и дифференциальные уравнения; алгебра, логика и геометрия; вычислительная математика и математическое моделирование; моделирование в социально-экономических системах; информационные системы и технологии; образование в области информатики и математики. Для участия в шестом конгрессе было отобрано 136 докладов по важнейшим вопросам науки и образования. В конференции приняли участие около 190 человек из 22 городов различных регионов Российской федерации и зарубежья. Участвовало более двадцати докторов наук и семидесяти кандидатов наук. В конгрессе активное участие приняли молодые исследователи, преподаватели вузов и учителя учреждений среднего образования. Около 25% всех докладов сделаны молодыми исследователями. В рамках VI Конгресса был проведен конкурс работ молодых ученых. Каждая работа была представлена под девизом и прошла двойное рецензирование докторами наук. Победители конкурса удостоены премии Лауреата конкурса работ молодых ученых памяти С. В. Ковалевской. Работа Конгресса освещалась в средствах массовой информации ГТРК «Красноярск», на сайтах ИВМ СО РАН, СибГТУ и СФУ.
(Отдел прикладной информатики)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., проф. В. В. Слабко (СФУ)
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. А. Н. Горбань
«МНС-2010» проводилcя при поддержке РФФИ с 15 по 17 октября 2010 г. на базе Института вычислительного моделирования (ИВМ СО РАН) (Красноярск, Академгородок). К началу семинара издан сборник материалов «Моделирование неравновесных систем -2010», Красноярск, 258 с.
Проблема моделирования неравновесных систем — одна из важнейших проблем современной науки, возникающая на стыке математического моделирования, физики, химии, биологии, социальных наук. Семинар является единственным регулярным научным мероприятием за Уралом, посвященным этой проблеме. Для многих участников, особенно молодых, семинар представляет одну из немногих возможностей для профессионального общения в области их научных интересов, первой попыткой публичного выступления с результатами своих исследований, и их профессионального обсуждения.
Цель семинара — объединение усилий специалистов различных областей науки. Общение на семинаре позволяет взглянуть на конкретную проблему с точки зрения различных областей науки и найти новые, нетрадиционные подходы к ее решению.
Проведение такого семинара в Красноярске связано с успехами красноярских исследователей в моделировании неравновесных физико-химических, биологических, медицинских, технических и социальных систем; наличием большого числа квалифицированных специалистов в данных областях.
На семинаре были представлены 66 докладов от 93 авторов/соавторов из различных регионов Российской Федерации и СНГ, а также Института Кюри, Франции. Материалы семинара опубликованы к началу его работы.
Принято решение о продолжении ежегодного проведения семинаров с обязательным привлечением большего числа студентов и молодежи.
Основные публикации:
- Моделирование неравновесных систем — 2010. — Материалы конференции. — Красноярск. — 2010. — 258 с.
(Отдел моделирования неравновесных систем)
| К началу | |
Проект РФФИ №
Руководители: член-корреспондент РАН В.В. Шайдуров В. В., д.ф.-м.н., проф. В. М. Садовский
С 12 по 14 октября 2010 г. в Институте вычислительного моделирования СО РАН (Академгородок, г. Красноярск) при финансовой поддержке РФФИ проводилась VII межрегиональная школа-семинар «Распределенные и кластерные вычисления». Она посвящена развитию и применению распределенных и параллельных вычислительных технологий в различных областях науки и техники. Научная программа VII школы включала в себя следующие направления: проблемы математического моделирования на базе многопроцессорных вычислительных систем; параллельные вычисления при моделировании динамики сложных дискретных систем; параллельное программирование в мультимедийных системах, обработке сигналов и изображений; управление параллельными вычислениями; инструменты для создания и использования параллельных программ; проблемы удалённого доступа к вычислительным ресурсам.
В работе школы-семинара приняли участие более 80 человек, в основном из городов Сибирского региона. География конференции: ИВМ СО РАН (г. Красноярск); ИВТ СО РАН (г. Новосибирск); ИГиЛ СО РАН (г. Новосибирск); ИДСТУ СО РАН (г. Иркутск); Институт прикладной математики им. М. В. Келдыша РАН (г. Москва); Институт Теплофизики СО РАН (г. Новосибирск); Томский государственный университет (г. Томск); Институт математики, экономики и информатики ИрГУ (г. Иркутск); Сибирский федеральный университет (г. Красноярск); КГПУ им. Астафьева (г. Красноярск); ООО Торинс (г. Красноярск); Оренбургский государственный университет (г. Оренбург); Ошский государственный университет (г. Ош, Киргизия). На школе был сделан 31 доклад, в том числе 8 лекций приглашенных ведущих ученых. Бурное обсуждение среди участников вызвали вопросы, связанные с перспективой развития многопроцессорных вычислительных систем с гибридной архитектурой (кластерных систем в сочетании с графическими устройствами). В рамках школы был проведен семинар по технологии CUDA. На закрытии школы принято решение о повышении ее статуса до Всероссийского уровня. Были достигнуты соглашения по взаимодействию в организации школ и конференций по аналогичной тематике с представителями Томского, Иркутского, Новосибирского и Кемеровского научных центров и университетов.
Основные публикации:
- Распределенные и кластерные вычисления // Тез. докл. VII Межрег. шк.-сем. — Красноярск: ИВМ СО РАН. — 2010. — 66 с.
(Отделы Вычислительной математики, Вычислительной механики деформируемых сред)
| К началу | |
Проект РФФИ №
Руководитель: д.ф.-м.н., проф. В. М. Садовский
«IV Европейская конференция по вычислительной механике» (ECCM 2010) проходила в г. Париже, во Дворце конгрессов с 16 по 21 мая 2010 года. Конференция была посвящена вопросам разработки и применения вычислительных методов к решению задач механики деформируемых сред и связанных с ними инженерных задач. В соответствии с программой конференции было сделано более 2000 докладов специалистами в области вычислительной механики, математического моделирования и многопроцессорных вычислений. В основном — из Франции, Германии, Австрии, Италии, Испании, Англии, США, Канады, Португалии, Швеции, Польши, Греции, а также Китая, Японии, Австралии и др. стран, в том числе около 40 участников из России (Москва, Санкт-Петербург, Новосибирск). На конференции были представлены 5 пленарных и 40 полупленарных лекций приглашенных специалистов.
В. М. Садовский участвовал в работе конференции с устным секционным докладом «Математическое моделирование движений сыпучей среды с застойными зонами» на минисимпозиуме «Вычислительные технологии для задач с большими деформациями». В докладе были представлены новые результаты, касающиеся исследования математических моделей упругопластических и сыпучих сред, а также моментных упругих сред. Основной инструмент исследования — параллельные вычислительные технологии с применением многопроцессорных вычислительных систем. Были проведены расчеты, точность которых недостижима для обычных персональных компьютеров и рабочих станций с последовательной архитектурой.
Представленные результаты были получены в рамках выполняемого в ИВМ СО РАН проекта РФФИ №
Основные публикации:
- Sadovskiy V. M.
On Mathematical Modeling of Granular Flow with Stagnant Zones // IV European Conf. on Computational Mechanics: Solids, Structures and Coupled Problems in Engineering (ECCM 2010). CD-ROM Proceedings. France, Paris: Springer. — 2010. — 2 p. - Sadovskaya O. V., Sadovskiy V. M.
Numerical Analysis of Elastic Waves Propagation in the Framework of Cosserat Theory // IV European Conf. on Computational Mechanics: Solids, Structures and Coupled Problems in Engineering (ECCM 2010). CD-ROM Proceedings. France, Paris: Springer. — 2010. — 11 p.
(Отдел вычислительной механики деформируемых сред)
| К началу | |
Грант РФФИ
Руководитель: к.т.н. Т. Г. Пенькова
X Международная конференция по информатике (the 10th International Conference of Computational Science 2010, ICCS), посвященная вопросам разработки и внедрения передовых информационных технологий и методов в различных сферах человеческой деятельности, проходила с 31 мая по 2 июня 2010 г. в Амстердаме, Нидерланды при поддержке Computational Science University of Amsterdam.
В 2010 году ICCS отмечала десятую годовщину «Celebrating 10 years of Advancing Computational Thinking». В связи с этим событием были приглашены ученые мирового уровня Стефан Вольфрам (Stephen Wolfram), Сез Ллойд (Seth Lioyd), Антон Зелингер (Anton Zeilinger), Питер Хантер (Peter Hunter), Лазло Барабази (Laszlo Barabasi), Эд Зейдель (Ed Seidel) для представления докладов о настоящем и будущем информатики.
Средства финансирования, выделенные РФФИ, использованы для оплаты транспортных расходов на поездку. Участвуя в работе конференции, руководитель проекта, Т. Г. Пенькова, выступила на рабочем семинаре «Представление знаний» с устным докладом «On-line analytical processing based on Formal concept analysis».
Основные публикации:
- Korobko A., Penkova T.
On-line analytical processing based on Formal concept analysis // Procedia Computer Science. — 2010. — V. 1. — № 1. — P. 2305–231 1.
(Отдел прикладной информатики)
| К началу | |