ИВМ СО РАН Поиск 
Отчеты ИВМ СО РАН

Отчет ИВМ СО РАН за 2011 год

Программы фундаментальных исследований Сибирского отделения РАН

IV.29. Системы автоматизации, CALS-технологии, математические модели и методы исследования сложных управляющих систем и процессов


Программа IV.29.1. Теоретические основы и методы информационных и вычислительных технологий проектирования и принятия решений

Координаторы программы: академик РАН Ю. И. Шокин, член-корреспондент РАН В. В. Шайдуров

Проект IV.29.1.2 «Информационно-вычислительные технологии для анализа и проектирования сложных систем в ближнем космосе»
№ гос. регистрации 01201056404

Научный руководитель проекта: член-корреспондент РАН В. В. Шайдуров

Блок 1. Моделирование отклика магнитосферного хвоста на резкое падение динамического давления солнечного ветра, связанное с приходом к границе магнитосферы Земли фронта магнитного облака, движущегося от Солнца. Аналитико-численное исследование диффузионной области магнитного пересоединения в рамках двухжидкостной магнитогидродинамической модели (Н. В. Еркаев, В. В. Денисенко, А. В. Китаев).

Разработана аналитическая холловская магнитогидродинамическая модель стационарного магнитного пересоединения в сжимаемой плазме. Показано, что задача сводится к решению уравнения Града-Шафранова относительно магнитного потенциала. Получено решение, на основе которого исследовано формирование двойных электрических слоев, а также слоев пониженной плотности плазмы. Показано, что двойные электрические слои располагаются вдоль сепаратрис, отделяющих пересоединившиеся магнитные силовые от непересоединившихся. Вне двойных слоев условие квазинейтральности плазмы выполняется с большой точностью.

Исследованы эффекты, связанные с прохождением фронта падения давления вдоль магнитосферного хвоста. Показано, что резкий перепад давления на фронте приводит к резкому нарушению равновесия плазменного слоя и образованию перетяжек, приводящих к неустойчивости.

Усовершенствована математическая модель проникновения электрических полей и токов в ионосферу с поверхности Земли. Проанализирована наиболее популярная в настоящее время модель такого проникновения, включающая сторонние токи. Показано, что она не применима в земных условиях.

Блок 2. Разработка и отладка вычислительных алгоритмов, позволяющих менять параметры конструкции и режима работы элементов приборного блока космического аппарата во время проектирования (В. А. Деревянко, Е. Н. Васильев, А. В. Макуха, С. В. Кукушкин).

Разработан вычислительный алгоритм, интерфейс и программный комплекс «Panel Emulator» для расчетов теплового режима приборного блока космического аппарата негерметичного исполнения. В «Panel Emulator» расчетная часть и интерфейс полностью разделены и реализованы в разных программных компонентах, связанных между собой с помощью XML-схемы. Такая реализация обеспечивает простоту адаптации пакета для решения других сходных вычислительных задач. Математическая модель, положенная в основу «Panel Emulator», учитывает циклограммы включения приборов и нагревателей, динамику изменения внешних радиационных потоков при движении по орбите. Модель позволяет задавать сложную геометрию приборной сотовой панели с отверстиями и выступами.

Разработанный программный комплекс предоставляет конструктору удобный графический интерфейс, с помощью которого можно задавать конфигурацию приборов и элементов терморегулирования на поверхностях сотовой панели. «Panel Emulator» позволяет проводить для заданной конфигурации приборного блока моделирование теплового режима и наблюдать динамику изменения тепловых полей. Предусмотрена возможность отслеживания динамики изменения температуры в заданных точках поверхности и индикации перегрева приборов.

Работа выполнена в интересах ОАО «Информационные спутниковые системы им. ак. М. Ф. Решетнева», г. Железногорск.

Блок 3. Донное течение за летательным аппаратом в сверхзвуковом потоке (В. В. Шайдуров, Г. И. Щепановская, М. В. Якубович).

Изучено донное течение за летательным аппаратом при сверхзвуковом обтекании вязким теплопроводным газом. Предложена математическая модель на основе полных уравнений Навье-Стокса для двумерного случая. Дискретизация по пространству осуществляется методом конечных элементов. Метод траекторий применяется при аппроксимации по времени, впервые для всей системы уравнений Навье-Стокса. Из тестовых расчётов следует, что совокупность метода конечных элементов и метода траекторий позволяет построить экономичный алгоритм с вычислительной точки зрения. На рис. III.15 показано распределение поля скоростей за летательным аппаратом. Донное течение, получено по расчётным значениям за летательным аппаратом, обтекаемым сверхзвуковым потоком вязкого теплопроводного газа. Числа Маха и Рейнольдса равны соответственно M=2 и Re=2000. За телом образуется вихревая зона с отрицательными значениями скорости.

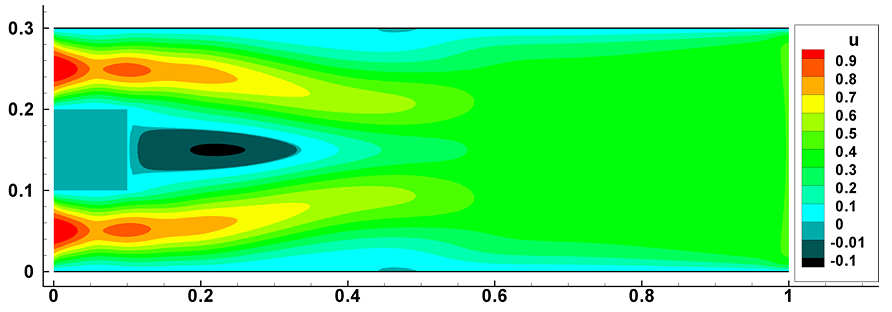
Рис. III.15
Рис. III.15. Распределение поля скоростей за летательным аппаратом

Блок 4. Построение кинетической квазиклассической теории трехмерного охлаждения и устойчивого удержания атомов и ионов с триподной системой квантовых переходов (типа F=1 > F=0) в частично когерентном световом поле.

I. Математическая модель локализации атомов в полихроматической оптической сверхрешетке (И. В. Краснов).

Построена квазиклассическая модель локализации атомов и ионов с триподной конфигурацией квантовых переходов в трехмерной (3D) диссипативной оптической сверхрешетке нового типа. Ее действие основано на эффекте выпрямления градиентной оптической силы в полихроматическом поле: специальной суперпозиции трехчастотного когерентного поля и частично-когерентного поля. Показано, что движение атомов в такой оптической сверхрешетке описывается кинетическим уравнением типа Фоккера-Планка для вигнеровской функции распределения атомов в фазовом пространстве или эквивалентной ему системой стохастических дифференциальных уравнений, учитывающих квантовые флуктуации оптических сил. Получено приближенное стационарное решение кинетического уравнения для невзаимодействующих частиц (движущихся в полихроматической решетке) в виде разложения по малому параметру — числу Кнудсена в данной задаче: отношению эффективной длины свободного пробега атомов в «вязком газе фотонов» к периоду решетки.

Это решение демонстрирует способность полихроматической сверхрешетки осуществлять эффективное охлаждение и сильную трехмерную пространственную локализацию триподных атомов и создавать кристаллоподобную систему локализованных сгустков атомов с хорошо управляемыми характеристиками (Рис. III.16, Рис. III.17). Другое, практически важное достоинство оптической сверхрешетки (вытекающее из решения кинетического уравнения): существование режимов охлаждения и локализации атомов, сочетающие в себе гигантские критические скорости (capture velocity) атомов, захватываемых в решетку с возможностью достижения субдоплеровских температур. Эти режимы локализации достигаются при медленном согласованном изменении интенсивностей полей (Рис. III.17).

II. Моделирование формирования ионных кулоновских кластеров в полихроматической оптической решетке (Л. П. Каменщиков, И. В. Краснов).

Ионные кластеры применяются в спектроскопии высокого разрешения, физике взаимодействующих кулоновских систем, квантовой информатике (хранение информации на квантовом уровне) и т.п.

Цель работы этапа: обоснование с помощью численного моделирования возможности формирования ионных кластеров в оптическом (лазерном) поле. При этом следует решить две проблемы: 1) охлаждение ионов до достаточно низких температур; 2) добиться пространственной локализации частиц (с долговременным удержанием) с учетом силы кулоновского отталкивания.

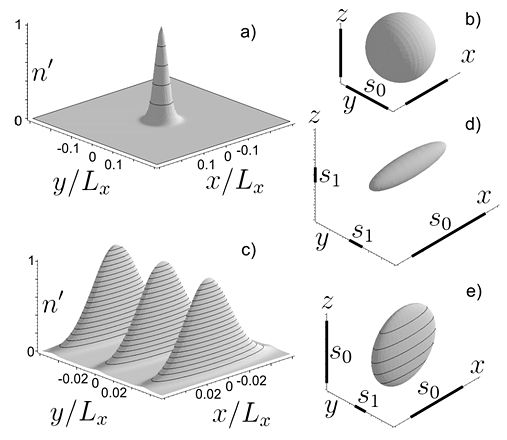
Рис. III.16
Рис. III.16. Типы пространственного распределения атомов в ячейках полихроматической сверхрешетки:
(a) и (c) — пространственные распределения атомов в плоскости z=0;
(b), (d) и (e) — области локализации атомов вблизи узлов сверхрешетки;
(a), (b) — $\textit{L${}_{x}/\lambda$}$= $\textit{L${}_{y}/\lambda$ = L${}_{z}/\lambda$ = }$2.7$\times$10${}^{4}$${}_{ }$;
(c), (d), (e) — $\textit{L${}_{x}/\lambda$}$ = 2.7$\times$10${}^{4}$; (d) — $\textit{L${}_{x}$/L${}_{y}$${}_{ }$ = L${}_{x}$/L${}_{z}$}$${}_{ }$ = 20;
(e) — $\textit{L${}_{x}$/L${}_{y}$}$${}_{ }$ = 20, $\textit{L${}_{x}$/L${}_{z}$}$${}_{ }$ = 1; $\textit{s${}_{0}$/L ${}_{x}$} \approx$ 0.05, $\textit{s${}_{1}$/L ${}_{x}$} \approx$ 0.01.

Низкие температуры получаются методом лазерного охлаждения ионов. Для пространственной локализации частиц ранее обычно использовались радиочастотные ловушки и статические электромагнитные ловушки (их недостаток: заметные паразитные движения). В 2010 г. была выдвинута идея локализации ионных частиц с помощью только оптических ловушек. В работах [1-2] показана перспективность освоения чисто оптических методов локализации ионов. В экспериментах Schneider'а и др. использовалась градиентная оптическая сила, порождаемая неоднородным монохроматическим лазерным излучением. В настоящей работе используем так называемые «выпрямленные градиентные силы» (rectified gradient forces) в полихроматическом лазерном поле с получением специальной пространственной конфигурации — полихроматической оптической сверхрешетки, предложенной работах [3-5].

Уравнения светоиндуцированного броуновского движения ансамбля взаимодействующих ионов в полихроматической оптической сверхрешетке выражают ньютоновский закон движения материальных частиц:

\[\; \; \; \; \; \; \; \; \; \; \; \frac{d{\rm r}_{i} }{dt} ={\rm v}_{i} {\kern 1pt} ,\; \; \; \; \; m\frac{d{\rm v}_{i} }{dt} ={\rm F}_{i}^{trap} +{\rm F}_{i}^{laser} +{\rm F}_{i}^{Coul} +{\rm F}_{i}^{stoch} ,\; \; \; \; i=1,{\kern 1pt} {\kern 1pt} .{\kern 1pt} {\kern 1pt} .{\kern 1pt} {\kern 1pt} .{\kern 1pt} {\kern 1pt} ,N,\]

где ${\rm r}_{i} $ и ${\rm v}_{i} $ — радиус-вектор и скорость $\textit{i}$-й частицы, ${\rm F}_{i}^{trap}, \; \; {\rm F}_{i}^{laser} $ — консервативная и диссипативная (трение) составляющие выпрямленной градиентной силы, ${\rm F}_{i}^{Coul} $ — кулоновская сила, действующая на $\textit{i-}$й ион со стороны всех других ионов, ${\rm F}_{i}^{stoch} $ — случайная сила (типа $\delta $-коррелированного гауссовского случайного процесса), обусловленная квантовыми флуктуациями и приводящая к диффузии в пространстве скоростей.

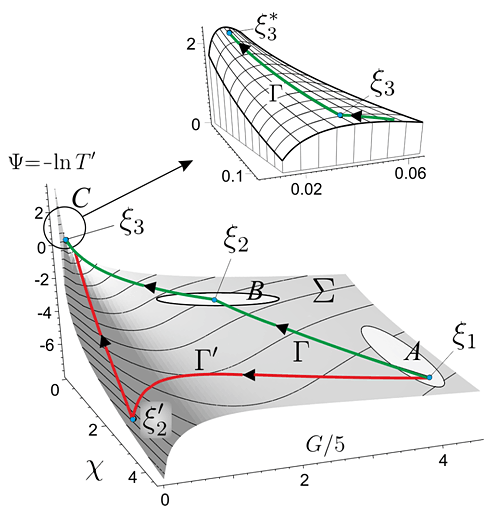
Рис. III.17
Рис. III.17. Зависимость относительной температуры атомов $\textit{T'}$ от управляющих параметров — безразмерных интенсивностей полей $\textit{c}$ и $\textit{G}$; $\textit{A}$, $\textit{B}$ — характерные области, соответствующие супердоплеровским температурам ($\textit{T'}$>>1), $\textit{C}$ — область субдоплеровских температур ($\textit{T'}$<1); $\textit{G}$ и $\textit{G'}$ — траектории устойчивого (без потери локализованных частиц) и неустойчивого перехода $\textit{A$\rightarrow$C}$. Область $\textit{A}$ характеризуется гигантскими значениями критической скорости частиц (velocity capture), при которой они могут захватываться в оптическую сверхрешетку

Численный пример. Проведен расчет движения ионов химического элемента иттербия в оптической решетке $3\times 3\times 3$ ячеек. В начальный момент в каждой ячейке среднего слоя (в плоскости $z=0$) были случайно разбросаны по шесть частиц с нулевыми начальными скоростями (рис. III.18 (а)), т.е. рассматривался ансамбль ионов из $N=54$ частиц. На рис. III.18 (б) показано положение частиц через $1.4{\kern 1pt} \cdot {\kern 1pt} 10^{-5} $c, а на рис. III.18 (в) — через $5.32{\kern 1pt} \cdot {\kern 1pt} 10^{-5} $с. При дальнейшем счете координаты частиц заметно не менялись, т.е. частицы достигали устойчивого состояния равновесия. Для решения системы дифференциальных уравнений применялся численный метод Штёрмера-Верле.


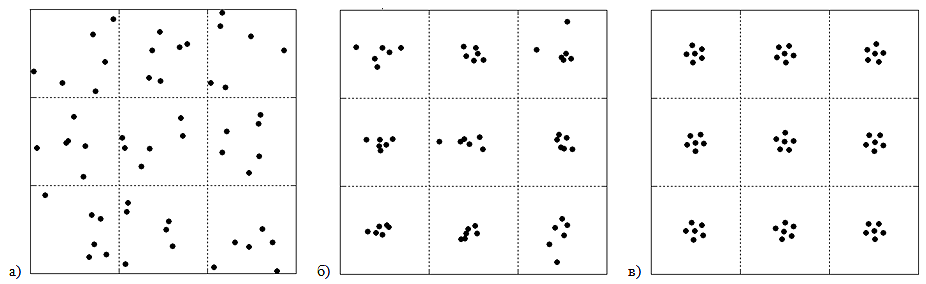
Рис III.18. Положение ионов в решетке в разные моменты времени

Построена вычислительная модель, описывающая формирование ионных кулоновских кластеров в полихроматической оптической сверхрешетке. Предварительные численные расчеты продемонстрировали принципиально новую возможность создания упорядоченного массива ионных кулоновских кластеров с помощью оптических сил в лазерном поле. В отличии от традиционных схем создания кластеров в радиочастотных ловушках и ловушках Пеннинга в предложенном методе отсутствуют паразитные движения типа микроосцилляций (с заметной энергией) или циклотронные и магнетронные вращательные движения. Отметим также, что построенная математическая модель позволяет рассчитывать реальные режимы формирования двумерных и трехмерных ионных кулоновских кластеров.

Основные публикации:

  1. Nieminen T. A.
    Optical Manupulation: Trapping ions // Nature Photonics, № 4, 2010, P. 737–738

  2. Schneider Ch., Enderlein M., Huber T., Schaetz T.
    Optical trapping of an ion // Nature Photonics, № 4, 2010, P. 772 775.

  3. Kazantsev A. P., Krasnov I. V.
    Rectification of the gradient force of resonant radiation pressure // JETP Lett., — 1987. — P. 332–336.

  4. Krasnov I. V.
    All-optical confinement of ultracold plasma with resonant ions // Phys. Lett.A, — 2009. — P. 2291–2297.

  5. Krasnov I. V.
    Three-dimensional localization of atoms in the polychromatic optical superlattice // Phys. Lett. A375. — 2011. — P. 2471–2478.

III. Численный анализ воздействия лазерного излучения на агрегат наночастиц (А. П. Гаврилюк).

На основе ранее построенной математической модели (см. A. P. Gavrilyuk, S. V. Karpov. Applied Physics B: v.97, issue 1, pp. 163–173, 2009) проведен (численно) систематический анализ эффектов воздействия лазерного излучения на агрегат наночастиц, представляющий собой пару (димер) связанных сферических металлических наночастиц одинакового радиуса, покрытых полимерным адсорбционным слоем. Было исследовано временное изменение параметров димера и, следовательно, изменения во времени его оптических характеристик под воздействием импульсного лазерного излучения с различной длиной волны, интенсивностью и длительностью импульса для разных начальных значений межчастичной щели. В частности, показано, что:

1) при интенсивностях, при которых начинают проявляться ПИФ (поляризационно-индуцированные силы), существенен нагрев электронов и кристаллической решетки частиц. Это означает, что необходимо в этих условиях учитывать термоэмиссию электронов из частиц димера;

2) фотомодификация димеров при умеренных плотностях энергии излучения, в основном, связана со смещением частиц внутри домена относительно друг друга. Это смещение обусловлено действием ПИФ и (или) плавлением полимерного слоя, происходящим при нагреве частиц;

3) чем меньше межчастичная щель димера, тем значительнее изменение его спектра при воздействии квазирезонансного лазерного излучения, то есть, меньше энергетический порог фотомодификации.

Основные публикации:

К блоку 1:

  1. Rubab N., Erkaev V., Biernat H. K., Langmayr D.
    Kinetic Alfven wave instability in a Lorentzian dusty plasma: Non-resonant particle approach // Physics of plasmas. — 2011. — V. 18 . — P. 73701. — doi: 10.1063/1.3599600.

  2. Erkaev N. V., Farrugia C. J., Harris B., Biernat H. K.
    On accelerated magnetosheath flows under northward IMF // Geophysical Research Letters. — 2011. — V. 38. — P. L01104. — doi: 10.1029/2010GL045998.

  3. Korovinskiy D.B, Semenov V. S., Erkaev N. V., Divin A. V., Biernat H. K., Mostl U. V.
    A 2.5 D electron Hall MHD analytical model of steady state Hall magnetic reconnection in a compressible plasma // Journal of Geophysical Research. — 2011. — V. 116 . — P. A05219. — doi: 10.1029/2010JA015942.

  4. Mostl U. V., Erkaev N. V., Zellinger M., Lammer H., Biernat H. K., Korovinskiy D., Groller H.
    The Kelvin-Helmholtz instability at Venus: What is the unstable boundary? // Icarus. — 2011. — V. 216. — P. 476–484. — doi: 10.1016/j.icarus.2011.09.012.

К блоку 2:

  1. Звонарь В. Д., Чеботарев В. Е., Фаткулин Р. Ф., Деревянко В. А., Васильев Е. Н., Деревянко В. В.
    Пакет прикладных программ для моделирования тепловых режимов приборных панелей космического аппарата негерметичного исполнения // XVI Междунар. науч. конф. «Системный анализ, управление и навигация». — Украина, Евпатория. — 2011. — С. 99–100.

  2. Научно-технический отчет «Комплексная адаптация пакета прикладных программ «Panel Emulator» для вычислительного моделирования тепловых режимов электронных приборов модуля специальных нагрузок», этап 9.4.3. — 2011. — 20 с.

К блоку 3:

  1. Шайдуров В. В., Щепановская Г. И., Якубович М. В.
    Применение метода траекторий и метода конечных элементов в моделировании движения вязкого теплопроводного газа // Вычислительные методы и программирование. — 2011. — Т. 12. — С. 275–281.

  2. Шайдуров В. В., Щепановская Г. И.
    О повышении точности приближённого решения уравнений Навье-Стокса для вязкого теплопроводного газа // Междунар. конф. «Современные проблемы прикладной математики и механики: теория, эксперимент и практика [Электронный ресурс]" . — Новосибирск: ИВТ СО РАН. — 2011. — № гос. регистрации — 0321101160, Режим доступа: http://conf.nsc.ru/niknik-90/reportview/39320, свободный. — Загл. с экрана (дата обращения: 15.07.2011).

  3. Chen H., Lin Q., Shaidurov V. V., Zhou J.
    Error estimates for triangular and tetrahedral finite elements in combination with trajectory approximation of first derivatives for advection-diffusion equations // Numerical Analysis and Applications. — 2011. — V. 4, № 4. — P. 345–362.

  4. Жоу Юнмин, Лин Кун, Чен Хонгтао, Шайдуров В. В.
    Оценки ошибки для треугольных и тетраэдральных конечных элементов в комбинации с траекторной аппроксимацией первых производных для уравнений адвекции-диффузии // Сибирский журнал вычислительной математики. — 2011. — Т. 14. — № 4. — С. 425–442.

К блокам 4:

  1. Krasnov I. V.
    Three-dimensional localization of аtoms in the polychromatic optical superlattice // Physics Letters A. — 2011. — V. 375. -Is. 24. — P. 2471- 2478.

  2. Краснов И. В., Шапарев Н. Я., Шкедов И. М.
    Задачи оптимального управления состояниям атомов в резонансном электромагнитном поле // Материалы IV Междунар. конф. «Математика, ее приложения и математическое образование (МПМО-11)». — Улан-Удэ. — Ч. I. — С. 52-57.

  3. Краснов И. В., Шкедов И. М.
    Моделирование режимов оптимального лазерного воздействия при двух- ступенчатой фотоионизации атомов // XV Междунар. науч. конф. «Решетнёвские чтения». — Красноярск. — 2011. — Ч. II. — С. 545–546.

  4. Каменщиков Л. П., Краснов И. В.
    Формирование ионных кулоновских кластеров в полихроматической оптической решетке // Материалы XIV Всерос. сем. «Моделирование неравновесных систем». — Красноярск: СФУ. — 2011. — С. 116–119.

  5. Gavrilyuk A. P., Karpov S. V.
    Dynamic changes of optical characteristics of resonant domains in metal nanoparticle aggregates under pulsed laser fields // Applied Physics B: Lasers and Optics. — 2011. — V. 102 (1). — P. 65-72. — doi: 10.1007/s00340–010-4180-x.

  6. Kosarev N. I., Shaparev N. Y.
    Imprisonment dynamics of resonance radiation in yases // J. Phys. B: At Mol. Opt. Phys.. — 2011. — V. 44. — Iss. 10. — P. 105402. — doi: 10.1088/0953–4075/44/19/195402.

  7. Kosarev N. I., Shaparev N. Y.
    Transfer of resonance radiation in an expanding sphere // J. Phys. B: At Mol. Opt. Phys. — 2011. — V. 44. — Iss. 19. — P. 195402. — doi: 10.1088/0953–4075/44/19/195402.

(Отделы Вычислительной математики, Вычислительной физики)

К началу

Webmaster