| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2011 год
Проекты СО РАН
- Междисциплинарные интеграционные проекты
- Проекты СО РАН, выполняемые совместно со сторонними научными организациями
- Заказной проект СО РАН
- Программа сибирского отделения РАН «Телекоммуникационные и мультимедийные ресурсы СО РАН»
- Программа сибирского отделения РАН «Высокопроизводительные вычисления СО РАН»
- Экспедиционные проекты СО РАН
- Лаврентьевский грант молодым ученым СО РАН
Лаврентьевский грант молодым ученым СО РАН
Проект № 1. «Математическое моделирование движения людей»
Руководитель проекта: к.ф.-м.н. Е. С. Кирик
Проведен анализ динамических и стохастических свойств полевой стохастической модели движения людей на характерных тестовых примерах. Исследование влияния вида пути показало, что наличие поворотов существенно снижает величину модельного потока в сравнении с потоком для прямого пути. Это согласуется с экспериментальными данными.
Выполнены вычислительные эксперименты по исследованию динамики дискретной модели в сужениях. Показано, что с изменением ширины сужения при всех прочих равных условиях величина удельного потока примерно постоянна, что согласуется с натурными наблюдениями. Установлена стохастическая устойчивость результатов моделирования: дисперсия времени эвакуации в среднем оказалась малой, а функция распределения времени эвакуации близка к нормальному закону.
На основе ранее полученных результатов разработана новая дискретно-непрерывная модель движения людей, непрерывная по пространству в выбранном направлении и дискретная с точки зрения количества возможных направлений перемещения. Уравнение движения получено в явном виде. Реализована схема параллельных расчетов эвакуации для больших зданий (схема распараллеливания по этажам), разработан корректный алгоритм обмена данными между процессорами.
Модель исследована численно на базовых примерах. В прямом коридоре (шириной м2 м) исследована динамика модели при периодичных граничных условиях. Показателем динамики служит величина удельного потока в контрольном сечении, $\textit{J${}_{мод}$=N}/\textit{T}/2$, где $\textit{N}$ = 1000 — контрольное количество человек, $\textit{T }$ — время, затрачиваемое на прохождение $\textit{N}$ человек через контрольное сечение. Показано, что на малых и средних плотностях модельный поток совпадает с данными натурных экспериментов (рис. V.40). Также отмечен тот факт, что с уменьшением скорости свободного движения совпадение модельного и экспериментального потоков наблюдается и при больших плотностях.
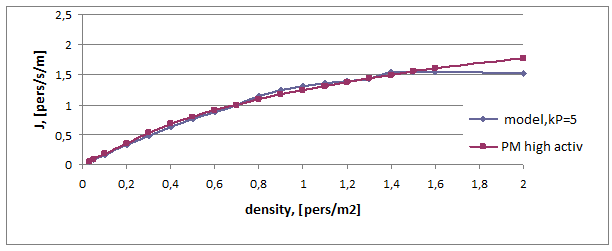
Рис. V.40. Фундаментальная диаграмма: модельные и экспериментальные данные
Область применения математических моделей движения людей — решение задач пожарной безопасности. В первую очередь они используются для моделирования эвакуации и определения времени эвакуации из зданий. Задавая различные условия (сценарии), можно составлять оптимальные схемы эвакуации, решать задачи по определению степени опасности текущих условий эксплуатации зданий, рассчитывать пожарные риски. Полученные результаты были использованы при создании учебного программного комплекса «Виртуальный тренажер по пожарной безопасности» для образовательных учреждений (рис. V.41). В дальнейшем планируется создание более общей модели, основанной на интеграции моделей движения людей и распространения пожара.
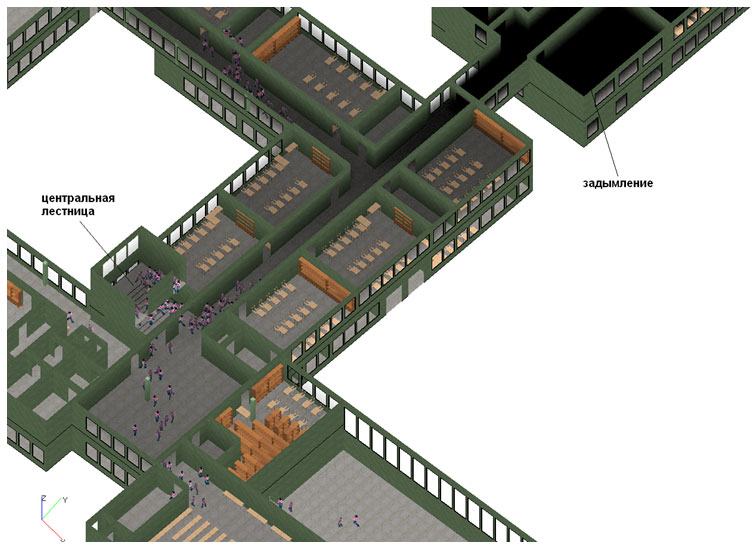
Рис.V.41. Трехмерная визуализация распространения дыма и эвакуации со второго этажа здания школы через центральную лестницу
Основные публикации:
- Кирик Е. С., Юргельян Т. Е., Малышев А. В., Дектерев А. А., ЛитвинцевК.Ю., Мельник А. А., Антонов А. В.
О формализации реакции человека на пожар и интеграция моделей эвакуации и развития ОФП // Проблемы безопасности и чрезвычайных ситуаций. — 2011. — Т. 3. — С. 59-68. - Юргельян Т. Б., Кирик Е. С., Круглов Д. В.
О чувствительности математической модели движения людей SIgMA.CA к геометрии пути // Журнал СФУ. Серия: математика и физика. — 2011. — Vol. 4. — № 4. — P. 556–568 . - Kirik E., Yurgel'yan T., Krouglov D.
On realizing the shortest time strategy in a CA FF pedestrian dynamics model // Cybernetics and Systems. — 2011. — V. 42 (1). — P. 1-15. — doi: 10.1080/01969722.2011.532636.
(Отдел моделирования неравновесных систем)
| К началу | |