| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2013 год
Федеральные программы
- Федеральная целевая программа «Поддержание, развитие и использование системы ГЛОНАСС на 20
12–202 0 годы» - Федеральная целевая программа «Развитие электронной компонентной базы и электроники на 20
08–201 5 годы» - Федеральная целевая программа «Развитие оборонно-промышленного комплекса Российской Федерации на 20
11–202 0 годы» - Федеральная целевая программа «Федеральная космическая программа России на 20
06–201 5 годы» - Федеральная целевая программа «Научные и научно-педагогические кадры инновационной России» на 20
09–201 3 годы - Комплексные проекты по созданию высокотехнологичного производства, выполняемые с участием российских высших учебных заведений
Федеральная целевая программа «Научные и научно-педагогические кадры инновационной России» на 2009–201 3 годы
Проект «Влияние диффузии и термодиффузии наночастиц на гидродинамику и теплообмен наножидкостей в мини- и микроканалах»
Руководитель: к.ф.м.н. И. И. Рыжков
Аннотация. Проект посвящен изучению влияния диффузии и термодиффузии (термофореза) наночастиц на течение и теплообмен наножидкостей в каналах. Для описания наножидкости используются уравнения Навье — Стокса, переноса тепла и массовой концентрации наночастиц. Впервые получено аналитическое решение задачи о распределении температуры и концентрации двухкомпонентной смеси в круглой трубе с течением Пуазейля и заданным потоком тепла на стенке. Исследовано влияние диффузии и термофореза наночастиц на вынужденную конвекцию наножидкости «вода — оксид алюминия» в трубе. Установлено, что термофорез приводит к снижению концентрации наночастиц вблизи стенки трубы. В результате вязкость и теплопроводность наножидкости в этой области также понижаются. Это приводит к снижению необходимого перепада давления в трубе и увеличению коэффициента теплоотдачи. Изучена зависимость локального и среднего коэффициента теплоотдачи от числа Пекле и интенсивности термофореза.
Наножидкость представляет собой двухфазную систему, состоящую из несущей жидкости (вода, этиленгликоль, масло) и наночастиц высокотеплопроводного материала (оксиды металлов, металлы, углеродные нанотрубки). Добавление наночастиц позволяет повысить теплопроводность базовой жидкости. Поэтому наножидкости могут эффективно использовать в качестве теплоносителя в системах охлаждения/обогрева. Основная цель проекта — исследовать влияние диффузии и термофореза наночастиц на течение и теплообмен наножидкостей в каналах. В рамках выполнения проекта были получены следующие результаты.
1. Проведен аналитический обзор научных работ в области наножидкостей в следующих направлениях: производство наножидкостей, механизмы переноса тепла, экспериментальные результаты и теоретические модели в области теплофизических свойств наножидкостей, вынужденная и естественная конвекция, математические модели для описания гидродинамики и теплообмена наножидкостей. На основе полученных сведений систематизированы экспериментальные данные по теплофизическим свойствам ряда наножидкостей.
2. Сформулирована математическая модель для описания наножидкостей, основанная на уравнениях Навье — Стокса, переноса тепла и массовой концентрации наночастиц с учетом эффектов диффузии и термофореза (возникновения потока наночастиц под действием градиента температуры). Двухкомпонентная модель описывает наножидкость как смесь базовой жидкости и наночастиц, концентрация которых является переменной величиной. Этим она отличается от однокомпонентной модели, которая предполагает, что наножидкость является однородной сплошной средой с физическими параметрами, соответствующими постоянной концентрации наночастиц. Уравнения двухкомпонентной модели имеют вид:
\[\partial _{t} {\rm (}\rho {\it u}{\rm )+}\nabla \cdot (\rho {\it uu})=\, -\nabla p+\nabla \cdot \Pi,~~~~~(II.1)\] \[\partial _{t} \rho {\rm +}\nabla \cdot (\rho {\it u})=\, 0,~~~~~(II.2)\] \[\partial _{t} {\rm (}\rho H{\rm )+}\nabla \cdot (\rho {\it u}H)=\, \nabla \cdot (\kappa \nabla T),~~~~~(II.3)\] \[\partial _{t} {\rm (}\rho C_{m} {\rm )+}\nabla \cdot (\rho {\it u}C_{m} )=\nabla \cdot (\rho DC_{m} +\rho D_{T} C_{m} \nabla T),~~~~~(II.4)\] \[\Pi =\mu \left(\nabla {\it u+}\nabla {\it u}^{T} -\frac{2}{3} \nabla \cdot {\it u}E\right),\, \, \, \, \, \, H=\int _{T_{0} }^{T}c_{p} dT.~~~~~(II.5)\]
Здесь $\textit{u}$ — вектор скорости, $p$ — давление, $\textit{T}$ — температура, $\textit{$C_{m}$}$ — массовая доля наночастиц, $\rho$ — плотность, $\mu$ — динамическая вязкость, $c_{p}$ — теплоемкость при постоянном давлении, $\textit{k}$ — коэффициент температуропроводности, $\textit{D}$ — коэффициент диффузии, $D_{T} $ — коэффициент термодиффузии, $\Pi $ — тензор вязких напряжений, $\textit{E}$ — единичный тензор, ${\it uu}$ и $\nabla {\it u}$ — диадные произведения, $\textit{H}$ — энтальпия, $\textit{T${}_{0}$}$ — характерное значение температуры. Предполагается, что физические свойства наножидкости являются функциями температуры и концентрации наночастиц. В случае однокомпонентной модели массовая доля наночастиц считается постоянной, а уравнение (II.4) исключается из рассмотрения.
3. Впервые получено аналитическое решение задачи о стационарном распределении температуры и концентрации бинарной смеси в круглой трубе с установившимся течением Пуазейля. На конечном отрезке трубы задан постоянный тепловой поток на стенке, в остальной части труба является теплоизолированной. Учитывается эффект термодиффузии. Показано, что с помощью специальных преобразований задача для определения концентрации сводится к задаче, которая полностью идентична задаче для нахождения температуры. Решение последней строится в виде ряда по собственным функциям самосопряженного оператора. Найдены решения для каждой из имеющихся подобластей (обогреваемый участок трубы, область перед ним и область за ним). Данная задача является существенным обобщением известной задачи Греца — Нуссельта для чистой жидкости. Полученные результаты применены для изучения влияния термодиффузии наночастиц на гидродинамику и теплообмен наножидкостей в мини-каналах.
4. Разработана методика расчета гидродинамики и тепломассообмена наножидкостей в каналах с учетом диффузии и термофореза наночастиц. Для численных расчетов используется программный комплекс ANSYS Fluent 14.5. Для расчета зависимости теплофизических свойств наножидкости от температуры и концентрации, а также для обработки расчетных данных (определения среднемассовой температуры и коэффициента теплоотдачи) разработан пакет подпрограмм на языке Си с использованием технологии функций пользователя.
5. Впервые исследовано влияние диффузии и термофореза наночастиц на вынужденную конвекцию наножидкости «вода — оксид алюминия» в трубе с заданным потоком теплоты на стенке. На основании анализа теоретических и экспериментальных результатов предложено выражение для коэффициента термодиффузии:
\[D_{T} =\alpha \frac{\beta _{T} }{\mu _{f} } \frac{\kappa _{f} }{2\kappa _{f} +\kappa _{p} } ,\]
где $\beta_{T}$ — коэффициент теплового расширения базовой жидкости, $\kappa_{f}$ и $\kappa_{p}$ — теплопроводность базовой жидкости и наночастиц соответственно, $\alpha$ — коэффициент пропорциональности, который выбирается таким образом, чтобы порядок численных значений $D_{T}$ соответствовал экспериментальным данным.
Выполнено численное моделирование вынужденной конвекции наножидкости в трубе с учетом переменных физических свойств. Жидкость поступает в трубу с заданной температурой и концентрацией наночастиц. Проведено сравнение численных результатов с точным решением. Обнаружено, что термофорез приводит к снижению концентрации наночастиц вблизи стенки канала. Это вызывает уменьшение вязкости наножидкости в пристеночном слое. В результате скорость движения вблизи стенки возрастает, что приводит к более интенсивному теплообмену в пристеночной области. Кроме того, снижение вязкого трения на стенке приводит к уменьшению требуемого перепада давления в трубе.
Зависимость локального коэффициента теплоотдачи от расстояния вдоль оси трубы показана на рис. II.5.
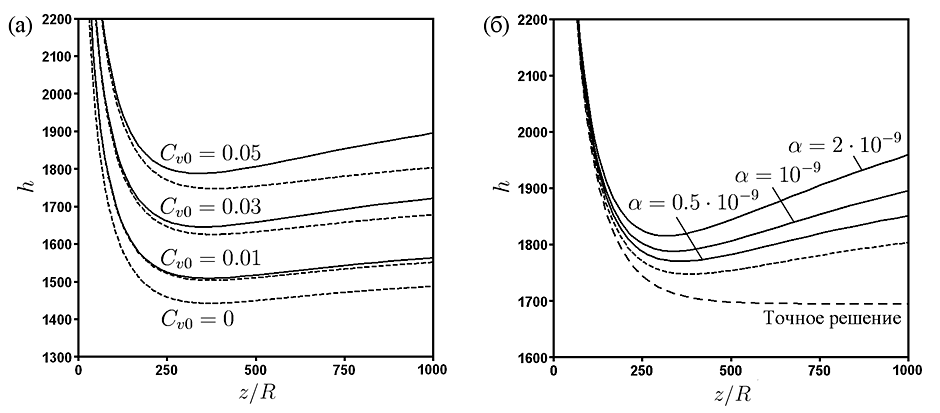
Рис. II.5. Зависимость коэффициента теплоотдачи от расстояния вдоль оси трубы для различных объемных концентраций наночастиц при $\alpha {\it =}10^{-9}$ (а) и для различных значений $\alpha$ при $C_{v}=0.05$ (б), ${\rm Pe}=2500$. Расчет на основе двухкомпонентной модели (сплошные линии), однокомпонентной модели (штриховые линии).
Этот коэффициент рассчитывался по формуле $h={q\mathord{\left/ {\vphantom {q \left[T(R,z)-T_{b} (z)\right]}} \right.} \left[T(R,z)-T_{b} (z)\right]}$, где $\textit{q}$ — поток теплоты на стенке, $T(R,z)$ — температура стенки, $T_{b} (z)$ — средняя температура по сечению. Для 5 % концентрации наночастиц увеличение локального коэффициента теплоотдачи может достигать 10 % по сравнению с результатами, полученными в рамках однокомпонентной модели. В этом случае снижение перепада давления составляет порядка 15 %.
На рис. II.6 приведена зависимость среднего коэффициента теплоотдачи от числа Пекле. Наибольшие отклонения результатов между расчетами по однокомпонентной и двухкомпонентной моделям наблюдаются при малых скоростях течения. Расчеты показали, что при 5 % концентрации наночастиц оксида алюминия средний коэффициент теплоотдачи возрастает примерно на 20 % по сравнению со случаем чистой воды.
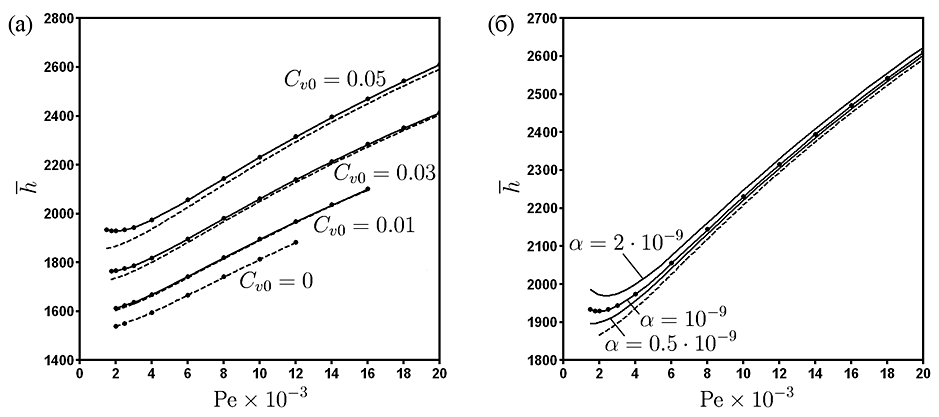
Рис. II.6. Зависимость среднего коэффициента теплоотдачи от теплового числа Пекле для различных объемных концентраций наночастиц (а) и для различных значений параметра $\alpha$ при $C_{v}=0.05$ (б). Расчет на основе двухкомпонентной модели (сплошные линии) и однокомпонентной модели (штриховые линии)
Основные публикации:
- Ryzhkov I. I.
The extended Graetz problem with specified heat flux for multicomponent fluids with the Soret and Dufour effects // Int. J. of Heat and Mass Transfer, 2013. — V. 66. — P. 461–471 . - Рыжков И. И., Минаков А. В.
Исследование процессов переноса тепла и наночастиц в наножидкости в условиях вынужденной конвекции // Материалы Открытой конф. молодых ученых. — Красноярск: ИВМ СО РАН, 2013. С. 123–131 .
(Отдел Дифференциальных уравнений механики)
| К началу | |