| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2013 год
Программы фундаментальных исследований сибирского отделения РАН
- III.22. Механика жидкости, газа и плазмы, многофазных и неидеальных сред, механика горения, детонации и взрыва
- IV.35. Когнитивные системы и технологии, нейроинформатика и биоинформатика, системный анализ, искусственный интеллект, системы распознавания образов, принятие решений при многих критериях
- IV.36. Системы автоматизации, CALS-технологии, математические модели и методы исследования сложных управляющих систем и процессов
- Проект IV.36.1.1. Разработка информационно-вычислительных моделей сложных динамических систем и процессов в ближнем космосе
- Проект IV.32.1.4. Разработка математических моделей сложных систем и процессов, их алгоритмическая и программная реализация на вычислительных системах высокой производительности
- IV.38. Проблемы создания глобальных и интегрированных информационно-телекоммуникационных систем и сетей. Развитие технологий и стандартов GRID
IV.36. Системы автоматизации, CALS-технологии, математические модели и методы исследования сложных управляющих систем и процессов
Программа IV.36.1. Новые решения проблем исследования и математического моделирования сложных динамических систем и процессов и их приложения в задачах проектирования, автоматизации и управления
Координатор программы: член-корреспондент РАН В. В. Шайдуров
Проект IV.36.1.1. Разработка информационно-вычислительных моделей сложных динамических систем и процессов в ближнем космосе№ гос. регистрации 01201356265
Научный руководитель проекта: член-корреспондент РАН В. В. Шайдуров
Блок 1.
Разработана динамическая вычислительная модель двухфазных контуров системы терморегулирования космического аппарата с пассивной циркуляцией теплоносителя (рис. III.12), позволяющая рассчитывать динамику температуры и давления в элементах контура при различных внешних условиях: подаваемой мощности к капиллярному насосу, мощности нагрева гидроаккумулятора и интенсивности охлаждения конденсатора. В качестве параметров модели задаются геометрические характеристики элементов контура, характеристики пористой структуры капиллярного насоса, условия охлаждения конденсатора и теплофизические характеристики теплоносителя. Использование динамической модели позволяет определять характеристики проектируемых двухфазных тепловых контуров с капиллярным насосом, а также разработать алгоритмы терморегулирования и стабилизации температуры области подвода теплоты.
На основе созданной вычислительной модели проведены расчеты зависимости параметров и инерционности контура от реальных внешних условий и режимов нагрева гидроаккумулятора (ГА). Определены значения температуры пара в области испарения в пористой структуре в зависимости от величины подводимой к контуру мощности $\textit{Q}$ при разных мощностях нагрева гидроаккумулятора $\textit{Q${}_{ГА}$}$ в условиях температуры $T\textit{${}_{priem}$} = -10{}^\circ C$ приемника теплоты (охлаждающей жидкости конденсатора).
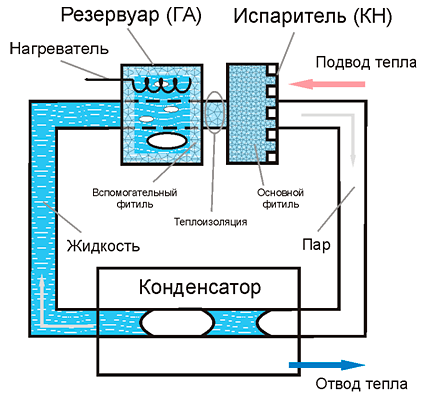
Рис. III.12. Схема двухфазного теплового контура с капиллярным насосом
На рис. III.13 показан пример стабилизации температуры $\textit{T${}_{v}$}$ при скачкообразных изменениях мощности $\textit{Q}$, компенсируемой изменением мощности $\textit{Q${}_{ГА}$}$. Проведенное вычислительное моделирование двухфазного теплового контура продемонстрировало принципиальную возможность терморегулирования области подвода теплоты с помощью нагревателя ГА.
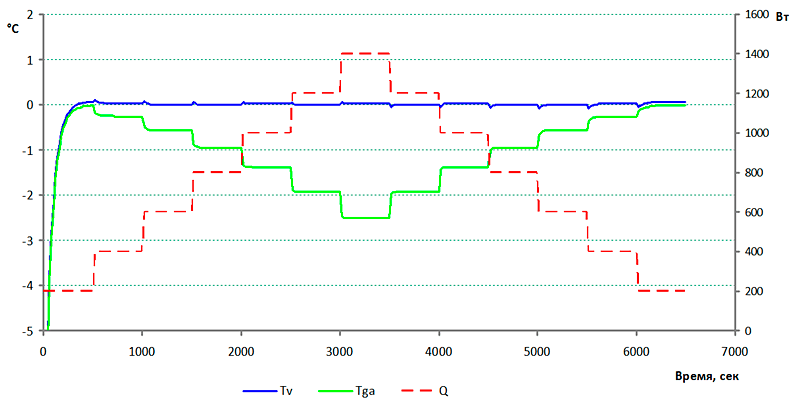
Рис. III.13. Поддержание постоянной температуры $\textit{T${}_{v}$}$ при изменении мощности $\textit{Q}$ компенсацией $\textit{Q${}_{ГА}$}$. Значение $\textit{T${}_{priem}$} = -10{}^\circ C$
Блок 2.
Продолжена разработка нового метода численного решения начально-краевой задачи для уравнений Навье-Стокса вязкого теплопроводного газа. Использование комбинации полу-лагранжевого метода при аппроксимации по времени и метода конечных элементов для дискретизации по пространству позволило уменьшить сложность построения дискретных аналогов на каждом временном слое и снять ограничение Куранта на соотношение шагов по времени и пространству. В частности, применение нового метода не требует согласования триангуляций на соседних временных слоях. Это значительно облегчает динамическое разрежение или сгущение триангуляций по пространству для оптимизации вычислительной работы или улучшения аппроксимации в пограничных слоях и ударных волнах. В итоге создан экономичный алгоритм для реализации на высокопроизводительных вычислительных системах.
Полученный пакет программ позволяет определять численное решение в широком диапазоне чисел Маха и Рейнольдса. Он использован для моделирования сверхзвукового обтекания клина в плоском канале вязким теплопроводным газом (рис. III.14 — III.15). Как следует из расчётов, за клином формируется зона нулевых и отрицательных значений скорости, и наблюдается резкое падение давления.
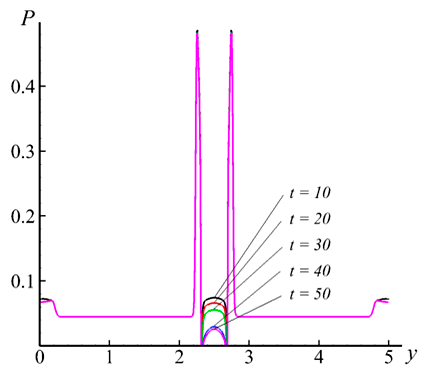
Рис. III.14
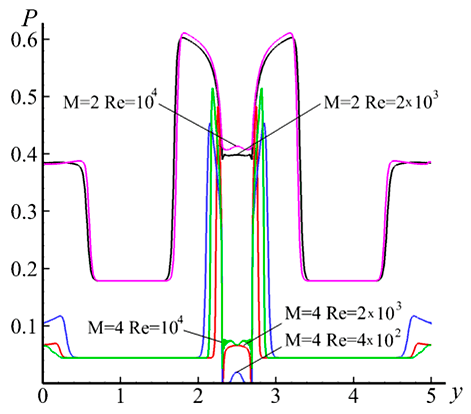
Рис. III.15
На рис. III.14 приведено распределение давления P в сечении канала, перпендикулярном набегающему потоку, вдоль основания клина для пяти моментов времени. Числа Маха и Рейнольдса равны M = 4 и Re = 2000. Угол полураствора клина равен $\textit{$\alpha$}= 45{}^\circ$. Из расчётов (рис. III.14) следует, что в угловых точках основания клина происходит отрыв потока и давление падает до нуля, потом вдоль основания клина давление имеет конечные значения и уменьшается с течением времени, что свидетельствует об увеличении протяжённости донного течения за клином. Давление в канале возрастает до максимальных значений при прохождении через головной скачок уплотнения.
На рис. III.15 приведено распределение давления P вдоль основания клина при обтекании потоком вязкого теплопроводного газа для различных чисел Маха и Рейнольдса в момент времени t = 20. С увеличением числа Маха давление вдоль основания клина резко уменьшается по сравнению с основным течением в канале, что соответствует экспериментальным представлениям.
Для оценки и сопоставления различных вариантов параллельных реализаций использовался алгоритм численного решения двумерного уравнения переноса полу-лагранжевым методом.
Для OpenMP-версии алгоритма проведено исследование влияния технологии HyperThreading, зависимости ускорения от размерности задачи и количества используемых потоков. Анализ результатов показал следующее.
- Накладные расходы, связанные с синхронизацией в OpenMP-версии, невелики.
- Для получения максимального ускорения OpenMP-версии программы выгодно использовать технологию HyperThreading (HT) с загрузкой максимально возможного количества логических ядер.
- Использование оптимизации компилятора существенно (больше, чем в 2 раза) уменьшает время работы последовательной программы.
Блок 3.
Создана математическая модель проникновения атмосферного электрического поля в ионосферу, в которой атмосфера и ионосфера рассмотрены как единый проводник с высотными распределениями компонент тензора проводимости, заданными в ионосфере в соответствии с современными эмпирическими моделями пространственно-временных распределений температуры и концентраций нейтральных молекул, ионов и электронов. Использованы также эмпирические модели изотропной проводимости в атмосфере. Пространственное распределение напряженности электрического поля построено как решение стационарного уравнения электропроводности с граничными условиями, соответствующими заданию у поверхности Земли вертикальной компоненты электрического поля и отсутствию электрического тока из ионосферы в магнитосферу (рис. III.16). Продемонстрировано, что электропроводность позволяет объяснить лишь слабое ионосферное электрическое поле с напряженностью порядка микровольта на метр. Добавление в модель оттока зарядов в магнитосферу еще уменьшает ионосферное поле.
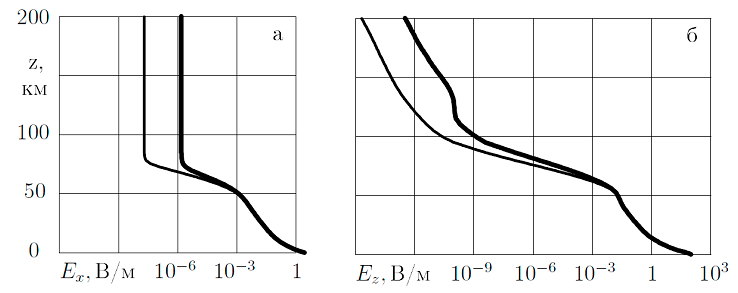
Рис. III.16. Модельные высотные распределения горизонтальной (а) и вертикальной (б) компонент напряженности электрического поля днем (тонкие линии) и ночью (жирные линии)
Разработанная ранее модель магнитного барьера применена к задаче обтекания солнечным ветром несимметричной магнитосферы Сатурна. На основе этой модели определены области неустойчивости течения на границе магнитосферы. Показано, что развитие неустойчивости приводит к существенному увеличению поступления энергии из солнечного ветра внутрь магнитосферы.
Выполнен анализ возмущений магнитосферы и ионосферы Земли, связанных с приходом корональных выбросов и магнитных облаков от Солнца. Для этих событий характерно значительное усиление межпланетного магнитного поля, что приводит к существенному увеличению толщины магнитного барьера вблизи границы магнитосферы. При этом увеличивается интенсивность магнитного пересоединения на границе магнитосферы, возрастает разность потенциалов электрического поля поперек полярной шапки, значительно возрастают магнитные возмущения в магнитосфере и ионосфере Земли.
Выполнен статистический анализ данных наблюдений об ускорении солнечного ветра в области обтекания магнитосферы Земли. Получено хорошее согласие статистических данных с разработанной математической моделью. Ускоренные потоки формируются вблизи магнитного экватора, как показано на рис. III.17.
Выполнены численные исследования магнитогазодинамической неустойчивости токового слоя магнитосферного хвоста при наличии отрицательного градиента нормальной компоненты магнитного поля. Получены зависимости инкремента от длины волны. Определены амплитуды возмущений на нелинейной стадии.
Получила дальнейшее развитие нестационарная гидродинамическая модель «убегания» атмосферного газа от планеты в окружающее пространство под действием приходящего жесткого ультрафиолетового излучения. На основе расчетов получены оценки интегрального потока частиц из атмосферы в окружающее пространство. В зоне редких столкновений гидродинамическая модель стыковалась с кинетической моделью, основанной на методе Монте Карло. Моделировалось взаимодействие нейтрального атмосферного газа с солнечным ветром с учетом процессов перезарядки. Показано, что в результате перезарядки возникают энергичные нейтральные частицы, движущиеся к планете и вызывающие дополнительный нагрев верхней атмосферы. Разработанные модели применялись для атмосфер различных планет.
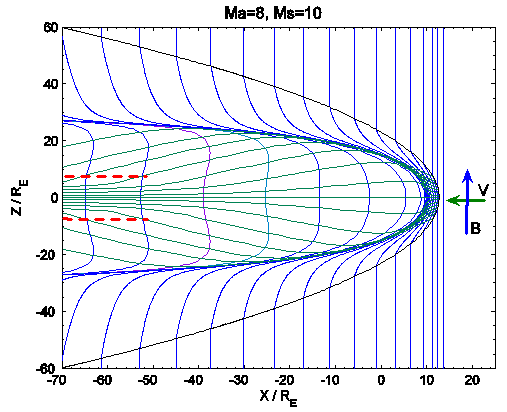
Рис. III.17. Картина обтекания магнитосферы в плоскости XZ, копланарной межпланетному магнитному полю, направленному вдоль оси Z. Зеленые кривые — линии тока на границе магнитосферы, синие кривые — магнитные силовые линии, огибающие магнитосферу. Ma — число Маха-Альфвена, Ms — газодинамическое число Маха. Черная кривая изображает фронт ударной волны. В окрестности магнитного экватора формируется ускоренная струя, границы которой обозначены красными штриховыми линиями
Блок 4.
Создана компьютерная модель динамики ионов в диссипативной оптической сверхрешётке (ДОС), основанная на численном решении стохастических дифференциальных уравнений ланжевеновского типа и методе Монте-Карло для вычисления математических ожиданий функционалов от решений. Модель учитывает кулоновские взаимодействия между ионами и действие на них резонансных оптических сил: диссипативных (трение) и консервативных составляющих выпрямленной градиентной силы, а также стохастических сил (типа дельта-коррелированного гауссовского случайного процесса), обусловленных квантовыми флуктуациями. Для вычисления фазовых траекторий ионов используется алгоритм Верле, модифицированный для учёта диссипативных и стохастических сил, и генератор случайных чисел с большим периодом ($10{}^{38}$), ориентированный на параллельные расчеты методом Монте-Карло. Программная реализация модели выполнена на языке DVM-Fortran-95 и предусматривает распараллеливание вычислений независимых реализаций случайного процесса.
Численные эксперименты проводились на суперкомпьютере МВС-100К в Межведомственном суперкомпьютерном центре РАН (г. Москва). При расчёте светоиндуцированной динамики двухионной системы на физических временах порядка нескольких секунд для числа реализаций случайного процесса $2{}^{18}$, количестве временных шагов $8\cdot 10{}^{7}$ и использовании 256 — 512 процессоров время счёта варьировалось от 12 до 24 часов. Эффективность распараллеливания вычислений достигала 0.9.
На основе разработанной компьютерной модели продемонстрирована принципиальная возможность формирования и удержания в ячейках ДОС двухионных (кулоновских) кластеров: системы из двух холодных ионов (с эффективной температурой порядка милликельвина) с фиксированным межчастичным расстоянием (с точностью до малых относительных флуктуаций) и положением центра масс. Параметр кулоновского взаимодействия (отношение энергии кулоновского отталкивания к кинетической энергии относительного движения ионов относительно друг друга) в рассмотренном случае ионов иттербия (Yb) достигал значений порядка 100 при весьма умеренных значениях интенсивности оптического излучения, не превышающей 1 Вт/см2. Ранее считалось, что подобные кулоновские кластеры можно получать только в электромагнитных ловушках (типа радиочастотной ловушки Паули или ловушки Пеннинга) и невозможно получить в чисто оптической ловушке из-за большой величины энергии кулоновского отталкивания в сравнении с реально достижимой глубиной обычных оптических монохроматических ловушек для атомных частиц. Продемонстрированный эффект основан на особенностях резонансных радиационных сил в полихроматических световых полях.
Рассмотрено прохождение резонансного излучения через расширяющуюся газовую среду, имеющую градиент скорости. Показано, что поглощение излучения в среде уменьшается, что связано с доплеровским смещением частоты поглощения, вызванным расширением среды. Определяющим фактором в данном процессе является соотношение между оптической толщиной стационарной среды $\tau {}_{0}$ и величиной $V_{{\rm R}} /V_{0}$ ($V_{{\rm R}}$ — скорость разлета газа, $V_{0}$ — тепловая скорость атомов). При $V_{{\rm R}} /V_{0} \gg \tau _{0}$ наступает просветление среды. Проанализирован также спектр резонансного поглощения ионов в расширяющейся ультрахолодной сферической плазме. С ростом величины $V_{{\rm R}}/V_{0}$ начальная оптическая толщина среды уменьшается и среда становится прозрачной. Для охлаждения ионов предлагается использовать внешнее резонансное излучение, уширенное в красную область спектра.
Показано, что для эффективного охлаждения ионов (с целью достижения сильнонеидеального состояния) необходимо сканирование отстройки лазерного излучения в зависимости от температуры ионов. Найдено выражение для зависимости от температуры отстройки лазерного излучения, обеспечивающей максимальный темп охлаждения. На основании этого выражения определены предельные значения параметра неидеальности ионов, которые могут быть достигнуты для заданных концентраций плазмы $n{}_{0}$ и температуры электронов $T{}_{e}$ (см. рис. III.18).
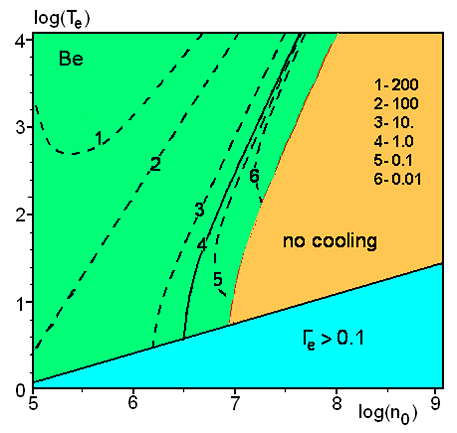
Рис. III.18. Область достижимых значений параметра неидеальности $\Gamma_{i}$ ионной подсистемы бериллиевой плазмы. Номерам кривых приведены в соответствие предельные значения $\Gamma_{i}$ при заданной концентрации плазмы $n_{0}$ и температуре электронов ${\rm T}_{e}$
Разработана математическая модель оптодинамики малых агрегатов (двух- и трехчастичных) плазмонно-резонансных наночастиц в поле импульсного лазерного излучения различной интенсивности, длины волны, поляризации и длительности импульса. В отличие от ранее разработанной модели в настоящей работе учтены такие важные факторы как полидисперсность наночастиц и изменение константы релаксации свободных электронов материала с изменением температуры и фазовым переходом (плавлением) нагреваемых излучением частиц. Разработанная модель позволяет исследовать процессы в агрегатах, состоящих из произвольного числа частиц. На основании численных расчетов (на примере серебряных наночастиц) выполнен сравнительный анализ влияния фактора локального окружения частиц домена и порождаемого этим окружением эффекта усиления локального поля на оптодинамические процессы в доменах и их фотомодификацию. Установлено, что учет вышеизложенных факторов (полидисперсность и плавление) приводит к существенным изменениям в описании оптодинамики и оптических характеристик систем связанных металлических наночастиц.
Блок 5.
В космическом машиностроении для изготовления высоконагруженных корпусных деталей двигателей широко применяют литейные алюминиевые сплавы. При этом чем выше степень измельчения структуры, тем выше механические свойства литых изделий и выше и надежнее эксплуатационные характеристики двигателя.
С целью измельчения структуры сплавов в процессе их приготовления либо в них вводят дополнительные центры кристаллизации (процесс называется модифицированием), либо блокируют рост зарождающихся кристаллов.
Применяющиеся в промышленности средства и способы модифицирования путем введения центров кристаллизации обладают рядом недостатков. В связи с этим разработан и успешно опробован в производственных условиях новый вид модификаторов — нанопорошки (НП) тугоплавких химических соединений, частицы которых имеют размеры не более 100 нм, что практически соответствует размерам центров кристаллизации. При этом НП вводят в жидкий металл в объеме отпрессованных прутков. Однако к настоящему времени содержание НП в прутках не удавалось довести выше 1.8 масс. %. С целью увеличения содержания в прутках НП, композицию, состоящую из алюминиевого порошка с размерами частиц 0.5-0.7 мм и НП нитрида титана TiN (который в предварительных экспериментах показал высокую зарождающую способность) с размерами частиц не более 40 нм, подвергали механоактивационной обработке в течение 5 мин в планетарной мельнице при 400 об/мин. Обработанную композицию прессовали в прутки. В результате были получены прутки, содержащие порядка 7.7 масс. % НП TiN. Эффективность модифицирующего воздействия полученных по новой технологии проверяли при литье деталей из широко применяющегося для литья корпусных деталей ЖРД алюминиево-кремниевого сплава АК12 (Al + 13% Si). При этом было установлено, что механические свойства существенно превышали ГОСТ 1583-93 (Таблица III.1).
| Прутки, отпрессованные по | Временное сопротивление разрушению, $\sigma{в}$ | Относительное удлинение, $\delta$, % | Твердость по Бринеллю, НВ | |||
|---|---|---|---|---|---|---|
| Величина, МПа | Прирост, % | Величина, % | Прирост | Величина, МПа | Прирост, % | |
| ГОСТ 583-93 | 157 | − | 2,0 | − | 500 | − |
| Патент 2475334 | 2 | 54,4 | 10,9-12,3 (ср. 11,6) | В 5,8 раз | 6 | 29,5 |
Таблица III.1. Механические свойства сплава АК12, модифицированного НП TiN
С целью блокирования роста кристаллов алюминиево-кремниевые сплавы обрабатывают фтористыми и хлористыми солями. Однако эффект их воздействия ограничивается 15-20 мин. Согласно разработанному способу в результате обработки расплава электрическим током (рис. III.19) эффект модифицирования солями может сохраняться до 2-х часов (Таблица III.2).
По ГОСТ 1583-93 свойства сплава АК12: $\sigma{в} \geq 150~МПа$; $\delta \geq 4.0 \%$; $НВ \geq 500$.
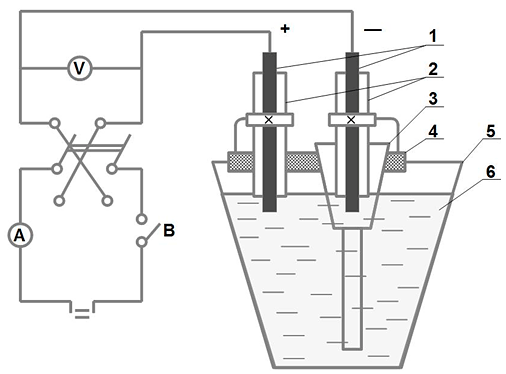
Рис. III.19. Схема наложения постоянного электрического тока при обработке жидкого сплава АК12: 1 — электроды; 2 — алундовые изоляторы; 3 — катодная ячейка; 4 — траверса; 5 — тигель; 6 — жидкий сплав АК12
| Вид обработки | Механические свойства | Свойства после модифицирования через, мин | |||||
|---|---|---|---|---|---|---|---|
| 0 | 20 | 40 | 60 | 90 | 120 | ||
| Без тока | $\sigma{в}$, МПа | 189 | 141 | 136 | 136 | 136 | 136 |
| $\delta$, % | 11,0 | 4,5 | 4,5 | 4,5 | 4,5 | 4,5 | |
| НВ | 718 | 535 | 517 | 517 | 517 | 517 | |
| Патент 2475550 [6] | $\sigma{в}$, МПа | 189 | 181 | 181 | 185 | 177 | 161 |
| $\delta$, % | 11,0 | 16,2 | 14,2 | 14,0 | 13,8 | 7,8 | |
| НВ | 718 | 688 | 688 | 703 | 673 | 612 | |
Таблица III.2. Механические свойства сплава АК12, обработанного постоянным электрическим током в жидком состоянии
Основные публикации:
- Деревянко В. А., Нестеров Д. А., Косенко В. Е., Звонарь В. Д., Чеботарев В. Е., Фаткулин Р. Ф., Сунцов С. Б.
Плоские тепловые трубы для отвода тепла от электронной аппаратуры в космических аппаратах // Вестник СибГАУ, 2013. — Вып. 6(52). — С. 111–116 . - Shaidurov V. V., Shchepanovskaya G. I., Yakubovich M. V.
Some new approaches to solving Navier-Stokes equations for viscous heat-conductive gas // Lecture Notes in Computer Science, 2013. — Vol. 8236. — P. 122–131 . - Denisenko V. V., Ampferer M., Pomozov E. V., Kitaev A. V., Hausleitner W., Stangl G., Biernat H. K.
On electric field penetration from ground into the ionosphere // J. of Atmospheric and Solar-Terrestrial Physics, 2013. — Vol. 102. — P. 341–353 . - Harris B., Farrugia C. J., Erkaev N. V., Torbert R. B.
Observational aspects of IMF draping-related magnetosheath accelerations for northward IMF // Annales Geophysicae, 2013. — Vol. 31(10). — P. 1779–178 9. - Shaparev N. Ya.
The spectrum of resonant laser radiation to decelerate ions in an expanding ultracold plasma // Laser Physics Letters, 2013. — Vol. 10. — P. 085501. - Крушенко Г. Г.
Патент РФ № 2 475 550. Способ модифицирования алюминиево-кремниевых сплавов и устройство для его осуществления / Бюл. 5. — 2013. Патентообладатель: ИВМ СО РАН.
(Отделы Вычислительной математики, Вычислительной физики)
| К началу | |
Проект IV.32.1.4. Разработка математических моделей сложных систем и процессов, их алгоритмическая и программная реализация на вычислительных системах высокой производительности
№ гос. регистрации 01201356261
Научный руководитель проекта: д.ф.-м.н., профессор В. М. Садовский
На основе разработанных ранее математических моделей и вычислительных алгоритмов создан программный комплекс, позволяющий численно решать на суперкомпьютерах с графической архитектурой плоские задачи о распространении упругих волн в блочном массиве, образованном упругими блоками c тонкими упругими или вязкоупругими прослойками (В. М. Садовский, О. В. Садовская, М. П. Варыгина).
Для описания деформации прослоек используются классические модели вязкоупругости Максвелла и Кельвина-Фойхта. Предполагается, что в начальный момент времени среда находится в естественном (ненапряженном) состоянии. На одной из границ действует распределенная или локализованная нагрузка в нормальном или касательном направлении. Граница, противоположная границе с заданными напряжениями, жестко закреплена. Боковые границы свободны от напряжений. Реализованы различные варианты задания внешней нагрузки: локализованная в системе точек или распределенная по участку границы, мгновенная или в виде последовательности импульсов. Параметры материала прослоек, такие как плотность, жесткость и коэффициент вязкости, а также тип прослоек могут быть различными, и задаются в исходных файлах программного комплекса.
При численном решении двумерных задач используется метод двуциклического расщепления по пространственным переменным. Для решения одномерных задач применяется монотонная ENO-схема, являющаяся обобщением схемы «распада разрыва» Годунова, с предельной реконструкцией решения на равномерной сетке. Графическое представление результатов осуществляется с помощью программы Paraview. Для анализа результатов численного решения строятся осциллограммы и сейсмограммы перемещений и скоростей на свободной поверхности и в центре тяжести блоков. При исследовании резонансных свойств блочной среды используется библиотека CUFFT для расчета быстрого преобразования Фурье.
Программный комплекс включает в себя последовательную и параллельную версии программ для графических суперкомпьютеров. Распараллеливание выполнено по технологии CUDA, позволяющей запускать задачу на множестве ядер графического устройства. Реализована возможность работы программного комплекса на нескольких GPU. Склейка решений, полученных на разных устройствах, осуществляется с помощью массивов, в которых хранятся значения скоростей и напряжений в прослойках.
Пример решения двумерной динамической задачи для блочного массива с тонкими прослойками представлен на рис. III.20. На левой границе действует П-образный импульс касательного напряжения (рис. III.20 а, б). В отличие от однородной среды в блочном массиве с прослойками возникает серия волн, отраженных от границ раздела. Данные расчеты выполнены на 448 CUDA ядрах для разного количества блоков, размерность задачи — 1024×2048 ячеек, материал блоков — горная порода, материал прослоек — грунт. Получены графики времен расчета задач на CPU, GPU и отношение времен CPU/GPU в логарифмической шкале в зависимости от размерности задачи (рис. III.20 в). По оси абсцисс на рисунке отложена размерность $N_{x}$ по одному из направлений, общая размерность задачи составляет $N_{x}^{2}$.
В рамках теории малых упругопластических деформаций однородной и изотропной пористой среды в замкнутой форме построены поля напряжений и перемещений в пористой среде в процессе разгрузки (В. М. Садовский, О. В. Садовская).
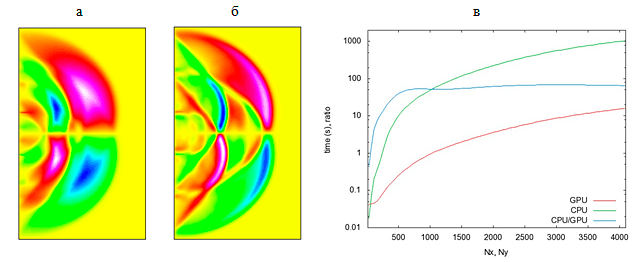
Рис. III.20. Распространение волн в блочном массиве с тонкими прослойками: линии уровня нормального напряжения для массива из 8 блоков (а) и 32 блоков (б); графики, характеризующие ускорение программ с распараллеливанием (в)
Показано, что при определенных условиях за упругой стадией разгрузки следует стадия повторного пластического течения с образованием зоны расширения пор, граница которой по мере понижения давления одновременно достигает границы зоны повторной пластичности и зоны схлопывания пор. Получены инженерные формулы для вычисления критических давлений предельного упругого состояния и предельного состояния среды с расширенными порами, а также формулы для определения радиусов раздела характерных зон пластичности и расширения пор при разгрузке. Разработана компьютерная программа в системе Matlab, автоматически выбирающая подходящий вариант расположения зон пластичности, схлопывания и расширения пор по входным параметрам задачи и позволяющая представить поля напряжений, перемещений, обратимых и необратимых деформаций в графическом виде (рис. III.21). Полученное решение используется при тестировании и верификации разрабатываемых программ для численного решения задач динамического деформирования пористых материалов на высокопроизводительных вычислительных системах.
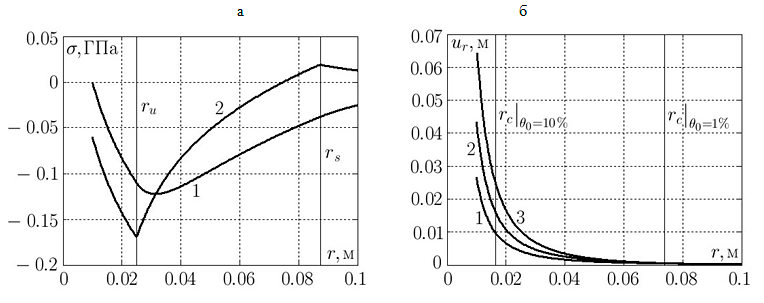
Рис. III.21. Расширение и схлопывание сферической полости: а — остаточные напряжения, б — остаточные перемещения
Разработана процедура построения смешанных дискретных моделей малой размерности для численного исследования статического напряженно-деформированного состояния пространственных конструкций из композитных материалов (А. Д. Матвеев).
Построены многосеточные конечные элементы для анализа микронеоднородных упругих сред. На этой основе проведены расчеты упругого деформирования многослойных оболочечных конструкций из композитов, применяемых в авиационной промышленности.
Для анализа предельного термоупругого поведения линейно-армированных композиционных материалов в рамках структурного подхода разработана модель ансамбля периодических ячеек высокопрочных волокон, внедренных в низкомодульную матрицу (С. Ф. Пятаев).
Термосиловое нагружение композиционного материала порождает однородное макронапряженное и неоднородное микронапряженное состояние. Макронапряженное состояние разделено на пять «базисных» более простых состояний. Для каждого из них методом конечных элементов получены соотношения для напряжений. Использование линейной комбинации этих решений позволяет по заданным макронапряжениям определить микронапряжения, удовлетворяющие классическому условию осреднения по объему. При построении критерия предельного упругого поведения композиционных материалов рассмотрено два варианта определения критических микронапряжений: во всём ансамбле (S) и в его центральной ячейке (s).
При определенных соотношениях на механические характеристики фаз полученные предельные поверхности оказались близкими к эллипсоидам или к ограниченным эллиптическим цилиндрам. На рис. III.22 представлены сечения $\gamma_{\Delta T}^{(s)}$ и $\gamma_{\Delta T}^{(S)}$ предельных поверхностей $P_{\Delta T}^{(s)}$ и $P_{\Delta T}^{(S)}$ для металлического и полимерного композиционных материалов в зависимости от темтературы $\Delta T=0.18^{0} {\rm C}$. Расчеты показали, что при нагружениях, близких к всестороннему обжатию в трансверсальной плоскости, полимерные композиционные материалы более чувствительны к виду осреднения, чем металлические. В полимерном материале это отличие достигает 25 %, тогда как в металлическом эта величина составляет примерно 4 %, что связано с меньшей разницей жесткостных характеристик компонент в металлических композиционных материалах по сравнению с полимерными.
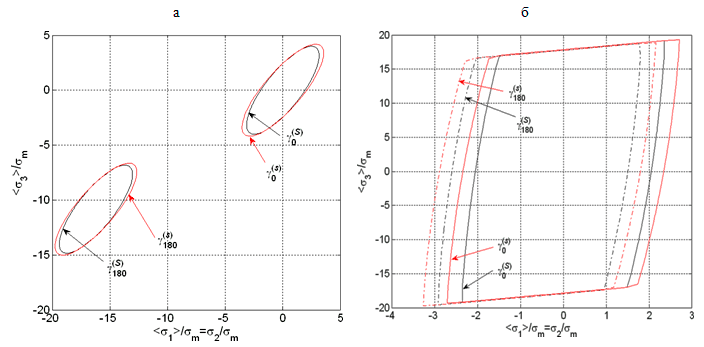
Рис. III.22. Сечения $\gamma_{\Delta T}^{(s)}$ и $\gamma_{\Delta T}^{(S)}$ поверхностей $P_{\Delta T}^{(s)}$ и $P_{\Delta T}^{(S)}$ плоскостью $\lt\sigma_{11}\gt = \lt\sigma_{22}\gt$ для металлического композита (а) и полимерного композита (б)
Разработана вычислительная методика для решения обратных задач мониторинга цунами на параллельных графических и гибридных вычислительных архитектурах (К. В. Симонов).
Методика включает в себя способ оценки основных параметров прогноза ожидаемого сильного цунамигенного землетрясения (времени, места и магнитуды) и контроля изменений этих параметров при поступлении новых данных о форшоках для выделенной очаговой области, а также вычислительные процедуры, позволяющие восстанавливать форму очага цунами по мареограммам на ближайших DART-станциях системы гидрофизического мониторинга распространения цунами в Тихом океане. Вычислительные процедуры реализованы на основе новых эффективных асимптотических формул для решения линеаризованной системы уравнений мелкой воды над неровным дном с локализованными начальными данными, полученных С. Ю. Доброхотовым и др. С помощью этой методики выполнены численные эксперименты по моделированию распространения волн цунами в акватории Тихого океана от сильных землетрясений в 20
Разработан и программно реализован оригинальный метод построения конечноэлементных сеток, привязанных к батиметрии, в сложных вычислительных областях для численного решения уравнений мелкой воды в морских акваториях мирового океана (Е. Д. Карепова, аспирант ИВМ СО РАН А. А. Ефремов, магистрант СФУ В. С. Волков).
Проблема получения даже равномерной достаточно мелкой сетки с батиметрией в заданной связной области с многосвязной границей является нетривиальной. В общем случае она усугубляется тем, что вблизи береговой линии в большинстве моделей сетку требуется сгущать. Кроме того, часто для метода конечных элементов необходимо строить триангуляции на выделенной области, отвечающей ряду нетривиальных свойств. В настоящее время существует множество программных продуктов (коммерческих и open source), решающих частично эту проблему, однако, каждый из них обладает недостатками. В рамках данного проекта разработана архитектура программного комплекса OceanTriangulator, которая основана на шаблоне проектирования Model-View-ViewModel, эффективно отделяющего бизнес-логику и логику представления от пользовательского интерфейса. Реализованы несколько алгоритмов как известных, так и новых. Среди них алгоритм чтения данных ограниченной области с масштабированием; алгоритм выделения областей (заливка); алгоритм выделения граничных точек, построение характеристической функции связной области с многосвязной границей; алгоритм выделения групп точек, составляющих замкнутую область; алгоритм построения контура связной области; алгоритм триангуляции Делоне; алгоритм триангуляции Делоне с ограничением на границах области. В реализации используется многопоточность, где это оправдано с точки зрения ускорения вычислений. На рис. III.23 представлены примеры построения сетки для расчетной области с помощью данного программного комплекса.
Построено неравенство для контроля устойчивости метода Ческино второго порядка точности. На основе стадий численной формулы разработан метод первого порядка точности с расширенным до 32 интервалом устойчивости. Сформулирован алгоритм переменного порядка и шага для решения умеренно жестких задач (Е. А. Новиков).
На основе стадий численной формулы Ческино и L-устойчивых (2,1)- и (2,2)-методов, а также схемы типа Розенброка второго порядка разработаны три алгоритма переменной структуры, в которых эффективная численная формула выбирается на каждом шаге по критерию устойчивости. Данные алгоритмы предназначены для решения как жестких, так и не жестких задач. Эффективность алгоритмов достигается при точности расчетов $10^{-2}$ и более.
Приведены результаты расчетов, подтверждающие работоспособность и эффективность построенных алгоритмов. На основе математической модели процесса разгона и движения электроподвижного состава с реостатно-контакторной системой управления тяговым электроприводом получен оптимальный закон управления двигателем постоянного тока, реализуемый дискретной системой управления (рис. III.24). Разработан алгоритм интегрирования уравнений движения, выбор шага в котором осуществляется с применением оценки аналога глобальной ошибки.
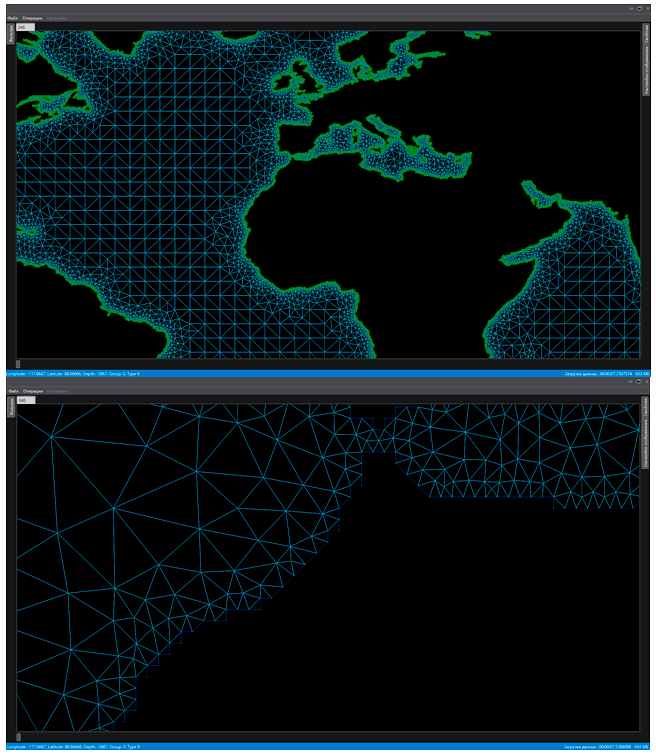
Рис. III.23. Пример триангуляции фрагментов акваторий Атлантического океана
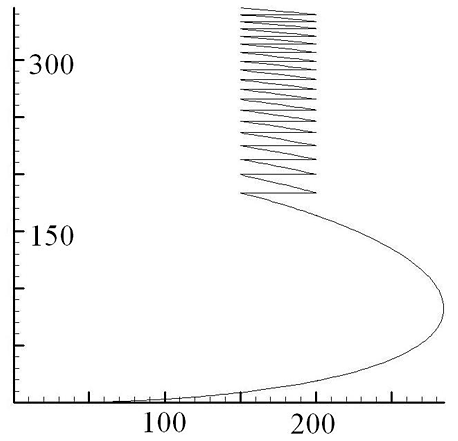
Рис. III.24. Зависимость скорости двигателя от тока якоря для троллейбуса ЗиУ-682-Г
Продолжена разработка эффективных алгоритмов и программ для вычисления гарантированных границ множеств решений обыкновенных дифференциальных уравнений с неточно заданными данными на высокопроизводительных ЭВМ (А. Н. Рогалев).
Проведен сравнительный анализ вычислительных схем, построенных на основе метода наименьших квадратов и минимаксного метода в задаче вычисления положения искусственного спутника Земли при ограничениях на ошибки измерений. Практическая значимость результатов анализа определяется тем, что не всегда ясно, насколько эффективен тот или иной подход к решению задачи: классический, при котором характеристики случайных ошибок исходных данных основываются на методе максимального правдоподобия, или неклассический (минимаксный), характеризуемый заданием лишь множеств принадлежности ошибок.
Результаты анализа позволили сделать несколько практических рекомендаций. Измерители наклонной дальности должны располагаться в углах треугольника, лежащего на поверхности Земли, близкого к равностороннему. Длины сторон треугольника должны быть выбраны так, чтобы линии визирования, исходящие их точек стояния измерителей и направленные в среднюю точку мерного интервала траектории, образовывали попарно прямые углы. Для случаев, когда данные получены с ошибками и информация об этом неполна, эффективно использовать алгоритм вариационно-взвешенных квадратических приближений. На примере модели наблюдения, соответствующей наихудшему распределению ошибок измерений, показано, что стандартное предположение о гауссовости снижает достоверность результатов о надежности и точности оценок параметров движения спутника.
Выполнено исследование параллельной реализации вычислительного алгоритма разработанной ранее стохастической модели движения людей при возникновении угроз пожарной безопасности в условиях дефицита времени и пространства (Е. С. Кирик, А. В. Малышев).
Вычислительная сложность алгоритма обусловлена большим числом (до нескольких тысяч на этаж) субъектов эвакуации, а также большим объемом данных, необходимых для расчета полей расстояний, общий объем которых может превышать лимит памяти в 4 Gb процесса с 32-разрядной адресацией. Используемая математическая модель допускает эффективный параллелизм как крупноблочный, так и мелкозернистый. Крупноблочное распараллеливание осуществляется разнесением между процессами расчетов движения людей на отдельных этажах с передачей данных о перемещениях с этажа на этаж. Этот подход решает проблему возможной нехватки памяти за счет распределения полей расстояний между несколькими процессами и позволяет более полно загрузить ядра процессора. Мелкозернистый параллелизм реализован при расчете движения людей на каждом этаже. Нити порождаются однократно в количестве, определяемом в зависимости от числа ядер, доступных приложению, и количества процессов, работающих над зданием.
Эффективность алгоритмов проверялась путем прямых замеров. Для экспериментов была выбрана задача эвакуации полностью заполненного большого зала БКЗ (Большого концертного зала) г. Красноярска. В зале 8 выходов, перед началом эвакуации в помещении находится 1025 человек. Первый эксперимент был поставлен на компьютере с 4-ядерным процессором Intel Core i5-760 под управлением ОС Windows 7 Pro x64. Второй эксперимент был поставлен на сервере с 4-мя 4-ядерными процессорами Quad-Core AMD Opteron-8378 (всего 16 процессорных ядер) под управлением ОС Windows Server 2008 R2. На рис. III.25 и III.26 приведены графики, показывающие ускорение и эффективность для таких конфигураций в зависимости от количества исполняющих нитей. Каждый расчет выполнялся три раза, замеренные времена решения задачи усреднялись.
Графики показывают динамику эффективности в зависимости от количества нитей. Ускорение достигает соответственно трех и десяти, что является существенным приростом. После того, как количество нитей становится больше количества ядер, происходит незначительный провал. Использование такой стратегии расчета нецелесообразно.
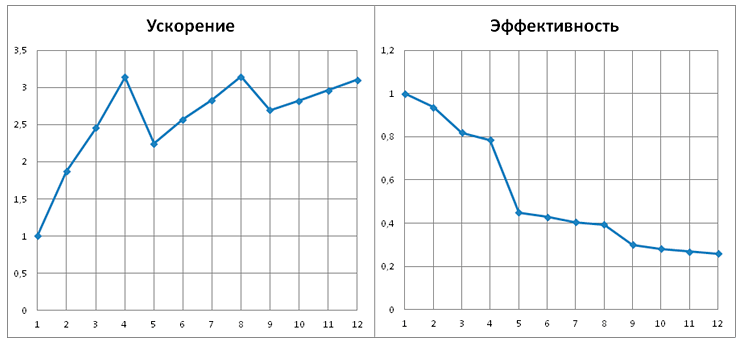
Рис. III.25. Ускорение и эффективность на 4 ядрах
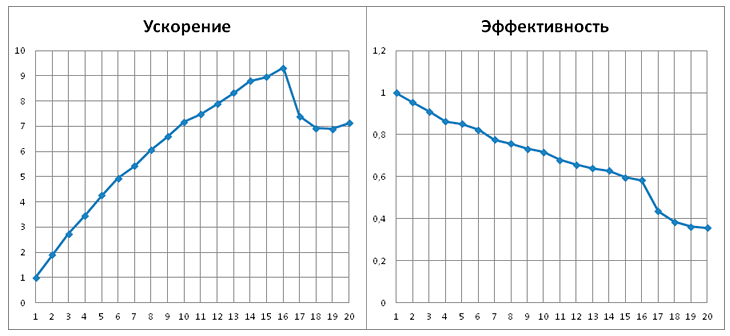
Рис. III.26. Ускорение и эффективность на 16 ядрах
Проведено детальное исследование вычислительных аспектов реализации метода сопряженных градиентов для решения систем линейных алгебраических уравнений (СЛАУ) с симметричной положительно определённой матрицей (И. В. Киреев).
В частности, исследовано решение СЛАУ, получаемое при использовании метода конечных элементов, при наличии ошибок округления. Рассмотрены как пошаговое поведение широко распространенных версий алгоритма, так и программно независимые критерии остановки итерационного процесса.
Основные публикации:
- Садовский В. М., Садовская О. В., Варыгина М. П.
Анализ резонансного возбуждения блочной среды на основе уравнений моментного континуума Коссера // РЭНСИТ: Радиоэлектроника. Наносистемы. Информационные технологии, 2013. — Т. 5. — № 1. — С. 111–118 . - Новиков Е. А.
Алгоритм интегрирования с применением методов типа Розенброка и Ческино // Вычислительные методы и программирование: новые вычислительные технологии, 2013. — Т. 14. — С. 254–261 . - Кочнев В. А.
Кинематико-гравитационная модель геодинамо // Геофизический журнал, 2013. — Т. 35(4). — P. 3-15.
(Отделы Вычислительной механики деформируемых сред, Вычислительной математики, Информационно-телекоммуникационных технологий)
| К началу | |