ИВМ СО РАН Поиск 
Отчеты ИВМ СО РАН

Отчет ИВМ СО РАН за 2000 год

Программы фундаментальных исследований СО РАН


Тема: «Алгебро-логические и теоретико-множественные исследования дискретных и случайных систем».

№ гос. регистрации 01.99.00 07784.

Научные руководители:
д.ф.-м.н., проф. В. К. Андреев; д.ф.-м.н., проф. О. Ю. Воробьев; д.ф.-м.н., проф. В. П. Шунков.


Построены фактор-системы уравнений микроконвекции в инвариантных переменных ранга 1 (17 систем) и ранга 2 (76 систем). Некоторые из систем проинтегрированы в квадратурах; им дана физическая интерпретация (А. А. Родионов, В. К. Андреев).
Показано, что основная группа Ли уравнений идеальной несжимаемой жидкости в сферической системе координат при наличии вращательной симметрии имеет нетривиальное расширение (В. К. Андреев).
В основном завершено построение теории T0-групп. Вышла из печати монография «T0-группы». Почти слойно-конечные группы без инволюций охарактеризованы в классе смешанных групп. Выяснено строение группы, разложимой в обобщенно-равномерное произведение примарных подгрупп. Построена смешанная группа Голода.
Для 18 из 26 спорадических групп решена проблема В. Д. Мазурова 7.30 из «Коуровской тетради» (В. П. Шунков, В. И. Сенашов, А. В. Тимофеенко).
Разработаны сет-вариационные методы поиска независимых разбиений конечного множества. Изучены теоретико-множественные структуры зависимости, порожденные вероятностными распределениями случайных конечных абстрактных множеств (СКАМ). Исследованы меры риска в качестве инструментов управления общим страховым процессом (О. Ю. Воробьев, А. А. Новоселов).

(Отдел вычислительной математики и нелинейных задач механики)

:

  1. Шунков В. П.
    Т0-группы. — Новосибирск: Наука. Сибирская издательская фирма РАН. — 2000. — 198 с.

  2. Сенашов В. И.
    Характеризация групп с обобщенно черниковской периодической частью // Мат. заметки. — 2000. — Т. 67. — Вып. 2. — С. 270–275.

  3. Тимофеенко А. В.
    Порядки произведений инволюций в порождающих некоторые простые группы тройках элементов порядка 2 // Труды международной конференции «Симметрия и дифференциальные уравнения». — Красноярск. — 2000. — С. 215–218.

  4. Шунков В. П., Сенашов В. И.
    Теория групп в Институте вычислительного моделирования СО РАН // Труды международной конференции «Симметрия и дифференциальные уравнения». — Красноярск: ИВМ СО РАН. — 2000. — С. 267–269.

  5. Воробьев О. Ю.
    Энтропийные методы случайно-множественного статистического анализа // Вычислительные технологии. — 1999. — Том 4. — С. 24-42.

  6. Воробьев О. Ю.
    Кусочно-независимый СКАМ ряд. — Красноярск: ИВМ СО РАН. — 2000. — 15 с. (Деп. ВИНИТИ 10.07.2000, № 1904-B00).

  7. Новоселов А. А.
    О пополнении системы предпочтений // Тез. Докл. I Всесибирского конгресса женщин-математиков. — Красноярск. — 2000. — С. 143.

  8. Новоселов А. А.
    Инвариантность характеристик процессов риска относительно преобразований параметров // Тезисы докладов III Всероссийского семинара «Моделирование неравновесных систем». — Красноярск: ИВМ СО РАН. — 2000. — С. 169–170.

  9. Новоселов А. А.
    Теория риска: принятие решений в условиях неопределенности // Тез. докл. III-го Всероссийского семинара «Моделирование неравновесных систем». — Красноярск: ИВМ СО РАН. — 2000. — С. 171–172.

  10. Новоселов А. А.
    О монотонности и выпуклости некоторых мер риска // Тез. докл. III Всероссийского семинара «Моделирование неравновесных систем». — Красноярск: ИВМ СО РАН. — 2000. — С. 173–175.

  11. Иванюкова И. В., Воробьев О. Ю.
    Визуализация статистических данных, заданных в абстрактном пространстве. — Красноярск: ИВМ СО РАН. — 2000. — 15 с. (Деп. ВИНИТИ 10.07.2000, № 1903-B00).

  12. Андреев В. К.
    Групповые свойства уравнений вращательно-симметричных движений идеальной жидкости // Труды II Международной конференции «Симметрия и дифференциальные уравнения». — Красноярск: ИВМ СО РАН. — 2000. — С. 14-17.

  13. Родионов А. А.
    Оптимальная система подалгебр второго порядка уравнений микроконвекции // Сб. Труды семинара «Математическое моделирование в механике». — Красноярск: ИВМ СО РАН. — 2000. — С. 120–130 (Деп. ВИНИТИ 06.06.00, № 1625–1300).

  14. Родионов А. А.
    Некоторые точные решения уравнений микроконвекции // Труды II Международной конференции «Симметрия и дифференциальные уравнения». — Красноярск: ИВМ СО РАН. — 2000. — С. 186–189.

К началу 2001 2000 1999

Тема: «Математическое моделирование и экспериментальное исследование структурной и функциональной организации водных экосистем на основе дисперсных границ раздела».

№ гос. регистрации 01.99.00 07793.

Научный руководитель:
д.ф.-м.н. В. Н. Лопатин.


Рассмотрены основные механизмы, формирующие структуру светового поля при взаимодействии зондирующего электромагнитного излучения с большими оптически мягкими (m<1,12) сферами. Оценены вклады различных геометрооптических потоков, формирующих интегральную индикатрису. Отмечена выраженная зависимость светорассеяния в заднюю полусферу от перераспределения энергии среди k-производных потоков. Доказано, что для оценки коэффициента асимметрии рассеяния непоглощающих частиц необходимо учитывать значительное количество таких потоков (~ 100). При этом выход на асимптоту происходит при очень больших значениях (фазовый сдвиг), в то время как для частиц с поглощением асимптотическое значение достигается гораздо быстрее. Аналитически получены геометрооптические асимптоты, на основе которых решается обратная задача светорассеяния (оценка значения показателя преломления исследуемых частиц). Показано, что полученные выводы и следствия во многом могут быть использованы для взвесей хаотично ориентированных сфероидов (Н. В. Шепелевич).
На основе теоретического и экспериментального исследований процессов фотосинтетического продуцирования в водных экосистемах качественно и количественно показано, что удельная поверхность клеток фитопланктона является важным фактором его продуктивности. Установлено, что содержание хлорофилла в единице биомассы связано с размерной структурой фитопланктонных сообществ и, в первую очередь, с соотношением площади поверхности клеток и их биомассы. Найден обобщенный структурный параметр, характеризующий размерное распределение сложных сообществ фитопланктона в наибольшей степени, чем отношение S/V. Показано, что ассимиляционная активность водорослей связана с относительным содержанием хлорофилла в биомассе и с размерным распределением клеток.
Разработана модель зависимости удельной продукции фитопланктонного сообщества от обобщенного структурного параметра, учитывающего соотношение между граничной поверхностью клеток водорослей и их объемом (биомассой). Модель позволяет оценивать первичную продукцию фитопланктона по дисперсной структуре сообщества независимо от видового состава и дает возможность выявлять закономерности функционирования водных экосистем и их устойчивости к факторам внешней среды на основе единого системного параметра (А. Д. Апонасенко, Л. А. Щур).
Разработана структура и сформирована база данных численности ихтиопланктона Красноярского водохранилища по репрезентативной выборке его представителей, в которую также включены данные по хемилюминесцентному мониторингу крови различных видовых популяций на экологически отличающихся участках водоема. Хемилюминесцентный мониторинг крови рыб позволяет проводить сравнение состояния системы иммуногенеза ихтиопланктона по ряду признаков: возрастному, половому, видовому, территориальному, зараженности паразитами; получить информацию о закономерностях изменения состояния системы иммуногенеза в зависимости от антропогенного фактора; выделить индикаторные, резистентные или наиболее чувствительные к данному типу загрязнения виды рыб; а также судить о природе факторов, определяющих экологическую ситуацию в целом (Г. В. Макарская).
Созданы основные компоненты ГИС-приложения, позволяющие работать с базой данных источников загрязнения (С. А. Ковязин., В. В. Касьянов), отображать их характеристики на фоне картографической информации, рассчитывать распределение загрязнений в приземном слое атмосферы, выбирать различные режимы состояния атмосферы, источников загрязнения (Б. А. Елгин, О. Э. Якубайлик, К. В. Теплицкий).

(Лаборатория биологической спектрофотометрии)

:

  1. Shepelevich N. V., Prostakova I. V., Lopatin V. N.
    Asymmetry Parameter for Large Optically Soft Spherical Biological Particles // J. of Biomedical Optics. — 2000.

  2. Щур Л. А., Апонасенко А. Д.
    О соотношении хлорофилла «а» и биомассы фитопланктона // Материалы Международной научной конференции «Фундаментальные проблемы воды и водных ресурсов на рубеже третьего тысячелетия». — Томск. — 2000. — С. 567–570.

  3. Макарская Г. В., Лопатин В. Н., Тарских С. В.
    Использование метода люминолзависимой хемилюминесценции клеток цельной крови в мониторинге состояния ихтиофауны // Материалы Международной научной конференции «Фундаментальные проблемы воды и водных ресурсов на рубеже третьего тысячелетия». — Томск. — 2000. — С. 545–547.

К началу 2001 2000 1999

Тема: «Развитие вычислительных методов решения задач математической физики»

№ гос. регистрации 01.99.00 07788.

Научные руководители:
чл.-корр. РАН В. В. Шайдуров, д.ф.-м.н., проф. В. М. Садовский.


Разработан новый экономичный метод решения нестационарной задачи Навье-Стокса для вязкой несжимаемой жидкости на основе метода расщепления по физическим процессам и геометрическим переменным. Дискретизация осуществляется с помощью одномерных конечных элементов произвольных порядков точности без нарушения устойчивости (В. В. Шайдуров, С. Ф. Пятаев, Е. Г. Быкова).
Проработан новый асинхронный подход для реализации некоторых алгоритмов линейной алгебры (умножение матриц, матрицы на вектор и т.д.) на вычислительном кластере, составленном из разнородных персональных компьютеров, находящихся в локальной сети. Получена числовая зависимость ускорения алгоритмов от скоростей передачи данных, быстродействия процессоров, обмена с дисковой памятью. Например, на кластере из десяти однородных персональных ЭВМ в сети Ethernet получено ускорение в 6.3 раза (В. В. Шайдуров, А. В. Малышев).
Для произвольного m получены оптимальные коэффициенты явных m-стадийных методов типа Рунге-Кутта первого и второго порядков точности для решения неавтономных систем обыкновенных дифференциальных уравнений средней жесткости, у которых согласованы области устойчивости основной и промежуточных численных схем (Е. А. Новиков).
Разработан эффективный вычислительный алгоритм для исследования задач динамики сыпучих сред на основе определяющих уравнений разномодульной теории упругости. В двумерной постановке выполнены расчеты распространения волн нагружения и разгрузки с образованием разрывов сплошности (рис. 1) (В. М. Садовский, И. О. Богульский).
Исследованы условия применимости адаптивного метода к решению задачи определения координат источника упругих колебаний в обращенном варианте вертикального сейсмического профилирования. Показано, что при соблюдении этих условий координаты источника могут быть найдены с точностью ± 10 м. Проведено сопоставление решения с результатами инклинометрии (В. А. Кочнев).
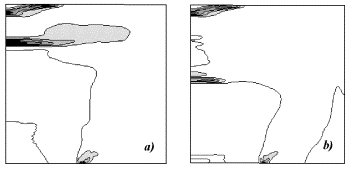
Самопроизвольное появление и схлопывание разрывов сплошности при распространении периодических волн
Рис. 1. Самопроизвольное появление и схлопывание разрывов сплошности при распространении периодических волн. С помощью разработанных ранее вычислительных алгоритмов для решения динамических контактных задач проведены расчеты высокоскоростного косого соударения деформируемых тел. Показано, что забегание пластической зоны, необходимое для образования волн на границе раздела, наблюдается только при скоростях точки контакта, меньших скорости диссипативных ударных волн (И. О. Богульский, В. М. Садовский, О. В. Садовская).

(Отдел вычислительной математики и нелинейных задач механики)

:

  1. Бехтерев И. С., Кочнев В. А., Гоз И. В., Поляков В. С.
    Метод решения навигационной задачи по сейсмическим данным ВСП ПБ // Геофизика. — 2000. — № 10.

К началу 2001 2000 1999

Тема: «Математическое моделирование гидродинамических процессов в жидких средах с границами раздела, гидротермических процессов».

№ гос. регистрации 01.99.00 07785.

Научный руководитель:
д.ф.-м.н., проф. В. К. Андреев.


Изучены плоские стационарные движения с учетом эффекта Соре, когда на свободной границе жидкости возможен аномальный термокапиллярный эффект (В. К. Андреев, М. В. Додонова).
Численно исследована устойчивость равновесия плоского слоя, когда происходит массообмен со свободной границей (В. К. Андреев, Е. А. Рябицкий).
Разработана версия метода частиц для несжимаемой жидкости, требующая существенно меньших ресурсов ЭВМ (быстродействие, память) по сравнению с исходным методом, в трехмерных задачах. Разработан более удобный и универсальный способ постановки граничных условий на жестких поверхностях с помощью «функций формы». Проведены расчеты тестовых двумерных задач струйного обтекания гладких контуров, а также некоторые расчеты трехмерного струйного обтекания шара (А. М. Франк).
На основе модели вязко-пластических сред Бингама разработан численный алгоритм для исследования динамики донных наносов. Сформулированы и решены две задачи: с заданной границей раздела подвижного и неподвижного слоев вязко-пластической среды и с неизвестной границей раздела. Выполнены модельные расчеты (В. М. Белолипецкий).

(Отдел нелинейных задач механики)

:

  1. Andreev V. K., Ryabitskii E. A.
    Perturbations of the Thermal Diffusion Motion of a Liquid with Free Boundary // Russ. Jour. Anal. Math. Modelling. — 2000. — Vol. 15. — № 2. — P. 111–125.

  2. Додонова М. В.
    Стационарные термодиффузионные течения плоского слоя // Труды II Международной конференции «Симметрия и дифференциальные уравнения». — Красноярск: ИВМ СО РАН. — 2000. — С. 91-94.

  3. Захватаев В. Е.
    Влияние изменений внутренней энергии межфазной поверхности на устойчивость двухслойного течения Пуазейля // Изв. РАН. МЖГ. — 2000. — № 6. — С. 16-26.

  4. Frank A. M.
    Discrete Modelling of a Liquid jet Suspending a Ball // Rus. J. of Numer. Analysis and Math. Modelling. — 2000. — Vol.15. — № 2. — P. 145–161.

К началу 2000 1999

Тема: «Моделирование процессов лазерного охлаждения и пространственной локализации ансамблей резонансных частиц».

№ гос. регистрации 01.99.00 07789.

Научный руководитель:
д.ф.-м.н., проф. Н. Я. Шапарев.


Построена модель кинетики лазерного охлаждения плазмы с учетом неупругих столкновений и трехчастичной рекомбинации. На ее основании показано, что в охлаждаемой резонансным излучением плазме возможно образование атомов в ридберговских и автоионизационных состояниях, а также надтепловых электронов. Причем роль этих процессов в охлаждении может быть значительной.
Построена модель механического действия слабых бихроматических полей на частицы с резонансным квантовым переходом j=0 — j=1. На основании этой модели показана возможность чисто оптического трехмерного конфаймента сгустков ультрахолодной плазмы (с резонансными ионами) в поле взаимно-ортогональных бихроматических стоячих волн.

(Отдел вычислительной физики)

:

  1. Gavrilyuk A. P., Krasnov I. V., Shaparev N. Ya.
    Laser Cooling of Rarefied plasma with Resonant Ions // Proceeding of the 5-th Russian-Chinese Symposium on Laser Physics and Laser Technology. — Tomsk. — 2000. — P. 6-12.

  2. Gavrilyuk A. P., Krasnov I. V., Polyutov S. P.
    Mechanical Action of Weak Bichromatic Fields on Particles with Resonant Quantum Transition j=0- j=1 // Proceeding of the 5-th Russian-Chinese Symposium on Laser Physics and Laser Technology. — Tomsk. — 2000. — P. 42-45.

  3. Gavrilyuk A. P., Krasnov I. V., Polyutov S. P., Shaparev N. Ya.
    About a Possibility of Ultracold Plasma Optical Confinement in weak Bichromatic Laser Fields // Proceeding of the 5-th Russian-Chinese Symposium on Laser Physics and Laser Technology. — Tomsk. — 2000. — P. 56-59.

К началу 2000 1999

Тема: «Mатематическое моделирование магнитосферных генераторов ионосферного электрического поля».

№ гос. регистрации 01.99.00 07786.

Научные руководители:
д.ф.-м.н. В. В. Денисенко, д.ф.-м.н. Н. В. Еркаев.


Построена математическая модель перестановочной неустойчивости магнитопаузы, учитывающая конечность толщины магнитопаузы и течение плазмы вдоль магнитопаузы (Н. В. Еркаев, И. Л. Аршукова).

(Отдел вычислительной физики)

:

  1. Arshukova I. L., Erkaev N. V., Biernat H. K.
    Instability of the Magnetopause with a Finite Curvature Radius and Velocity Shear // Geomagnetism International (submitted).

К началу 2001 2000 1999

Тема: «Моделирование неравновесных систем».

№ гос. регистрации 01.99.00 07787.

Научные руководители:
д.ф.-м.н., проф. А. Н. Горбань, д.ф.-м.н., проф. В. И. Быков.


На основе метода инвариантного многообразия предложен способ построения гибридных численных схем. Основу подхода составляют мониторинг и оценка отклонения от заданного макроскопического описания при микроскопическом интегрировании, сопровождающиеся переключением к интегрированию микроскопических уравнений при достаточно малой ошибке. Подход реализован для моделей растворов полимеров, когда микроскопическое интегрирование проводится в рамках броуновской динамики, а макроскопическое — в рамках интегрирования конститутивных уравнений (А. Н. Горбань, И. В. Карлин).
В течение 2000 г. продолжалась разработка алгоритма решения трехмерных уравнений Навье-Стокса в обобщенных криволинейных координатах методом конечных объемов на неразнесенной (неортогональной в общем случае) сетке, на которой все переменные локализуются в центрах контрольных объемов. Для моделирования турбулентности применяется двухзонная и стандартная k-epsilon модели турбулентности. Внедрены схемы типа TVD для аппроксимации конвективных членов. Реализованы граничные условия различных видов: вход потока, выход, плоскости симметрии (которые не обязаны быть параллельными каким-либо координатным плоскостям), неподвижные стенки, периодические условия. Для энтальпии задаются условия I-го, II-го или III-го рода. Реализовано задание напряжений на поверхности, что используется при моделированиии течения в водоемах под действием ветра. Проведено сравнение результатов моделирования с экспериментальными данными и с расчетами других авторов, показавшее хорошие результаты для ряда известных двух- и трехмерных тестовых задач, как изотермических (ламинарных и турбулентных), так и с учетом теплообмена и химических реакций. (В. И. Быков, Л. П. Каменщиков).

(Отдел вычислительной математики)

:

  1. Gorban, I. V. Karlin, V. B. Zmievskii, Dymova S. V.
    Reduced Description in Reaction Kinetics, Physica A. — 2000. — Vol. 275. — № 3,4. — P. 361–379.

  2. txt&zip  Zmievskii V., Karlin I. V., Deville M.
    The Universal Limit in Dynamics of Dilute Polymeric Solutions // Physica A. — 2000. — Vol. 275. — № 1,2. — P. 152–177.

  3. Каменщиков Л. П.
    Численное моделирование трехмерных стационарных дозвуковых ламинарных и турбулентных течений вязких газов и реагирующих газовых смесей в областях сложной конфигурации // Автореф. дис. ... канд. физ.-мат. наук. — Красноярск: ИВМ СО РАН. — 2000. — 21 c.

  4. Kamenshchikov L. P.
    Application of bounded higher-order schemes for numerical modelling of turbulent reactive flows in 3-D areas with curvilinear boundaries // Тез. докл. 4-го Сиб. конгресса по прикл. и индустр. мат-ке. — Нов-ск: ИМ СО РАН. — 2000. — Часть II. — С. 72.

К началу 2001 2000 1999

Тема: «Разработка математического и программного обеспечения многоуровневых интеллектуальных информационных систем принятия решений».

№ гос. регистрации 01.9.80. 007505.

Научные руководители:
д.т.н., проф. А. В. Лапко, к.т.н. Л. Ф. Ноженкова.


Исследованы непараметрические модели оценивания количественных характеристик законов условных распределений непрерывных случайных величин. На этой основе разработан ряд модификаций статистических алгоритмов анализа интервальных данных в задачах восстановления неизвестных зависимостей и имитационного моделирования пространственно распределённых систем (А. В. Лапко).
Разработаны алгоритмы и программы метода матричной прогонки для решения системы дифференциальных уравнений, описывающих нестационарные режимы процесса тепло-массообмена с рециркуляцией взаимодействующих потоков, проведены численные эксперименты (Н. Д. Демиденко).
Разработаны гибридные модели знаний, позволяющие выполнять геомоделирование с элементами активизации семантической информации ГИС. Модели относятся к продукционно-фреймовому типу с полисемантической интерпретацией. Особенностью модели является применение универсальных синтаксических конструкций для представления разных видов неопределенности.
Предложены методы построения статических и динамических параллельно-последовательно-альтернативных структур знаний, которые позволяют анализировать логические связи в системе продукций. Динамические структуры знаний применены для моделирования развития сложных сценариев и анализа последствий ЧС.
Предложена объектно-ориентированная реализация языка представления знаний. Разработаны алгоритмические и программные средства, предложена технология построения экспертных геоинформационных систем.
Выполнена апробация для задач предупреждения и ликвидации чрезвычайных ситуаций. Разработанные модели и программные средства применены также для создания интеллектуальной системы для проектирования микрополосковых фильтров (Л. Ф. Ноженкова).

(Отдел прикладной информатики)

:

  1. Volokitina A. V., Nozhenkova L. Ph., Sofronov M. A., Nazimova D. I.
    Prognosis of Emergency Situations under Wildland Fires based on Vegetation Fuel Maps. — Joint Fire Science Conf. And Workshop. Crossing the Millennium: Integrating Spatial Tech. And Ecol. Principles for a New Age of Fire Management. — 2000. — Vol. 1. — Р. 42-46.

  2. Беляев Б. А., Никитина М. И., Ноженкова Л. Ф., Тюрнев В. В.
    Интеллектуальная система для проектирования микрополосковых фильтров // Теория и системы управления. — 2000. — № 2. — С. 96–102.

  3. Волокитина А. В., Ноженкова Л. Ф., Софронов М. А., Назимова Д. И.
    Прогноз чрезвычайных ситуаций при пожарах растительности вблизи населённых пунктов // Материалы международной конференции «Сопряженные задачи механики и экологии». — Томск. — 2000. — C. 78-84.

  4. Демиденко Н. Д., Терещенко Ю. А.
    Численный метод решения краевых задач тепломассообмена // Информатика и системы управления. — Красноярск: КГТУ. — 1999. — Вып. 4. — С. 26-31.

  5. Косов Р. А., Лапко В. А.
    Непараметрические модели анализа интервальных данных // Информатика и системы управления. — Красноярск: КГТУ. — 1999. — Вып. 4. — С. 190–192.

  6. Лапко А. В., Лапко В. А., Крившич Д. В., Ченцов С. В.
    Непараметрические модели коллективного типа. — Новосибирск: Сибирская издательская фирма РАН «Наука». — 2000. — 190 с. (в печати).

  7. Ноженкова Л. Ф.
    Технология построения экспертных геоинформационных систем поддержки принятия решений по предупреждению и ликвидации чрезвычайных ситуаций // Автореф. дис. : докт. техн. наук. — Красноярск: ИВМ СО РАН. — 2000. — 42 с.

  8. Ноженкова Л. Ф., Шатровская Е. В.
    Применение структурной модели знаний для оценки риска аварий на промышленных объектах // Доклады III Всероссийской конференции с международным участием «Новые информационные технологии в исследовании дискретных структур». — Томск. — 2000. — С. 157–162.

К началу 2000 1999

Тема: «Разработка методов нейроинформатики».

№ гос. регистрации 01.99.00 07790.

Научный руководитель:
д.ф.-м.н., проф. А. Н. Горбань.


Разработаны методы Нейро-ГИС для визуализации и картографирования данных произвольной природы. В основе методов лежит подход, связанный с построением нейросетевых упругих карт.
Карта данных является моделью данных и одновременно подложкой, на которой помимо данных можно отображать различную сопутствующую информацию в виде цветных и полутоновых раскрасок. Реализован способ конвертирования изображения спроецированных данных вместе с раскрасками в переходный формат ГИС MapInfo. Это позволяет создавать атласы данных и раскрасок, а также открывает широкие возможности для использования методов ГИС.
На основе предлагаемой методики Нейро-ГИС разработан макет системы, предназначенной для анализа и визуализации экономических таблиц.
В качестве примера использования системы была взята таблица экономических показателей 200 крупнейших российских предприятий, полученная с официального интернет-сайта журнала «Эксперт».

(Отдел вычислительной математики)

:

  1. Зиновьев А. Ю., Питенко А. А.
    Визуализация данных методом упругих карт // Радiоелектронiка. Iнформатика. Управлiння. — Запорожье. — 2000. — № 1. — С. 76-85.

  2. Зиновьев А. Ю., Питенко А. А.
    Применение метода упругих карт для визуализации экономических показателей // Нейроинформатика и ее приложения. Материалы VIII Всерос. семинара. — Красноярск: КГТУ. — 2000. — С. 77-80.

  3. Gorban A. N., Rossiev A. A.
    Wunch II D. C. Neural Network Modelling of Data with Gaps // Радiоелектронiка. Iнформатика. Управлiння. — Запорожье. — 2000. — № 1. — C. 47-55.

К началу 2001 2000 1999

Тема: «Механика безопасности и остаточный ресурс технических систем и объектов».

№ гос. регистрации 01.99.00 07792.

Научный руководитель:
д.т.н., проф. В. В. Москвичев.


Разработаны перспективные направления использования модели «нагрузка-прочность» и пуассоновской модели отказов в задачах оценки конструкционного риска. В отличие от известных подходов в качестве базового элемента риск-анализа рассматривается потенциальная зона разрушения в конструкции. На этой основе выполнено разложение конструкционного риска на составляющие с выделением исходной компоненты — критериального риска. Эта компонента включает меру ущерба, связанную с разрушениями. Расчетное ядро риск-анализа включает оценку напряженно-деформированного состояния конструкции, выделение на этой основе потенциальных зон разрушений, построение моделей предельного состояния и оценку вероятностей (риска) разрушения при вариациях параметров моделей.
Для решения задач риск-анализа проведено теоретическое обоснование вида распределений критических размеров дефектов. Показано, что для случая хрупких разрушений функция распределения критических размеров трещин имеет вид закона Вейбулла, для квазихрупких разрушений вид гамма-распределения и для вязких разрушений — нормальный вид. На основе численного решения упругой и упругопластической задач механики разрушения проведены исследования вида распределений характеристик напряженно-деформированного состояния области дефектов типа трещин. Показано, что при вейбулловских вариациях размеров дефектов и нормальных вариациях напряжений функции распределения соответствуют нормальному закону или закону Вейбулла. Исследованы изменения параметров этих законов при вариациях числа экспериментов, параметров распределений дефектов и напряжений.
Разработаны расчетные алгоритмы риск-анализа конструкций по состоянию и по ресурсу. Риск-анализ по состоянию заключается в вычислении вероятности разрушения конструкции в заданный момент времени с учетом данных диагностики и сопоставлении этой вероятности с допустимым значением. Риск-анализ по ресурсу заключается в прогнозировании среднего безопасного ресурса или остаточного безопасного ресурса с учетом допустимого риска разрушения. Также получены формулы для оценки среднего безопасного ресурса и остаточного ресурса для случаев хрупких, квазихрупких и вязких разрушений.

(Отдел машиноведения)

:

  1. Доронин С. В.
    Ресурс крупногабаритных конструкций в условиях аварийных ситуаций // Тез. докл. V научн. конф. «Современные методы математического моделирования природных и техногенных катастроф». — Красноярск. — 1999. — С. 117–119.

К началу 2000 1999

Webmaster