| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2004 год
Программы РАН
- Президиум РАН
- Отделение математических наук
- Проект № 8 «Организация хранения и алгоритмические средства обработки больших массивов текущих навигационных параметров космических аппаратов системы ГЛОНАСС»
- Проект № 9 «Разработка и исследование вычислительных алгоритмов решения уравнений Навье-Стокса вязкой несжимаемой жидкости и их применение к задачам гидрофизики»
- Отделение физических наук
- Отделение энергетики, машиностроения, механики и процессов управления
Отделение математических наук
Программа № 1.3
«Вычислительные и информационные проблемы решения больших задач»
Научный руководитель:
д.т.н. Л. Ф. Ноженкова
Предложен подход к организации хранения эфемиридно-временной информации навигационных космических аппаратов (НКА), основанный на базовой концепции хранилищ данных, что делает возможным использование новейших наработок в этой области. Получены оригинальные методические и алгоритмические результаты в области организации хранения больших объемов данных. В силу специфики решаемой задачи потребовалось ввести ряд новых понятий, а также разработать специальные алгоритмы по предобработке исходных данных, хранимых в файлах формата RINEX. Это позволило работать с файлами RINEX теми же средствами и методами, что и с традиционными форматами баз данных.
Реализован рабочий макет интегрированной информационной системы, выполняющей функции сбора, хранения и предварительной обработки измерений текущих навигационных параметров НКА, полученных по сети беззапросных измерительных станций в виде RINEX-файлов. Система построена на базе технологии хранилищ данных. Разработан и реализован интерфейс доступа к данным, представленным в файлах формата RINEX. Программно интерфейс реализован в виде компонента, который позволяет формировать набор данных в виде таблицы с количеством полей по числу категорий данных, хранящихся в исходном файле. Число полей, из которых формируется таблица, можно настраивать в зависимости от потребностей задачи.
Предложенные методические и программные средства хранения и обработки больших объемов данных измерений позволяют более эффективно решать задачи оценки и повышения точности прогноза навигационных характеристик космических аппаратов.
Основные публикации:
- Жучков Д. В., Исаева О. С., Ишенин П. П., Никитина М. И.
Применение технологии хранилищ данных в задачах оценки точности определения навигационных характеристик космических аппаратов // Красноярск: ИВМ СО РАН. — 2004. — 28 с. (Деп. в ВИНИТИ 06.10.04, № 1570-В2004). - Жучков Д. В., Исаева О. С., Никитина М. И.
Организация сбора и хранения измерений текущих навигационных параметров космических аппаратов // Материалы VIII Всерос. науч. конф. «Решетневские чтения». — Красноярск: СибГАУ. — 2004. — С. 211–212 .
(Отдел прикладной информатики)
| К началу | |
Программа № 1.3
«Вычислительные и информационные проблемы решения больших задач»
Научный руководитель:
чл.-корр. РАН В. В. Шайдуров
Для выяснения степени влияния гравитационных и собственных колебаний Мирового океана на параметры вращения Земли был разработан математический аппарат, в основе которого лежит гидродинамическая модель мелкой воды в гидростатическом приближении по вертикали. В результате трехмерные уравнения Навье-Стокса сводятся к системе нестационарных двумерных уравнений на сфере, в которых учитываются сила тяжести и сила Кориолиса. Для исключения сингулярности в дифференциальных уравнениях, обусловленной особенностью географической системы координат, был осуществлён переход в новую сферическую систему координат, полюсные особенности которой располагаются на территории Гренландии и Антарктиды. Приближенное решение системы дифференциальных уравнений (часто называемой приливными уравнениями Лапласа) было получено с помощью метода конечных элементов. В качестве конечных элементов использовались элементы, линейные на треугольниках.
Поскольку используемая гидродинамическая модель океана физически состоятельна лишь на глубинах более 30 м, то расчётная область рассматриваемых задач имеет сложную многосвязную структуру. Основываясь на открытой батиметрической базе данных ETOPO5, была построена характеристическая функция этой области. Предварительно сглаженные глубины океана брались с пятиминутным разрешением по широте и долготе с последующей интерполяцией внутри сферического четырехугольника.
На языках ANSI C и FORTRAN 77 был разработан комплекс программ топологического анализа двумерных областей, заданных своими характеристическими функциями. Результатом так называемая «маска» двумерной области, отправляясь от которой выполнялась триангуляция Мирового океана, рис. 1 (Л. П. Каменщиков, И. В. Киреев, С. Ф. Пятаев).
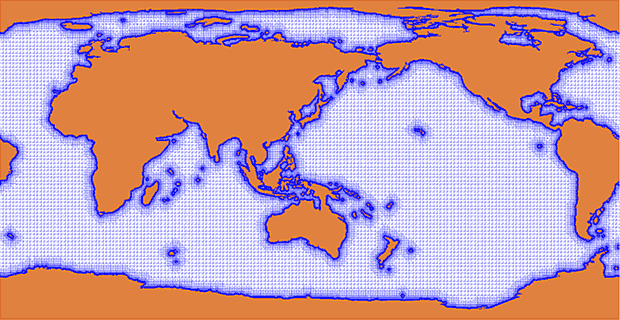
Рис. 1. Триангуляция Мирового океана.
Разработаны численный алгоритм и компьютерная программа для исследования ветровых течений в стратифицированных водоемах (2-D модели). Компьютерная модель основана на специально разработанной библиотеке С++ классов для решения дифференциальных уравнений с частными производными. Библиотека содержит классы для описания геометрии водоема; для построения расчетной сетки и доступа к информации о ней; для осуществления сборки разреженной матрицы и ее решения. Написана подпрограмма, реализующая построение нерегулярной сетки. Численные расчеты позволили установить зависимость горизонтальных и вертикальных распределений гидрофизических переменных от геометрии водоема, силы ветра и стратификации (В. М. Белолипецкий, С. Н. Генова).
Основные публикации:
- Белолипецкий П. В., Генова С. Н., Грицко В. В.
Компьютерная модель вертикальной структуры водоема // Вычислительные технологии. — 2004. — Т. 9. — Вестник КазНУ им. аль-Фараби. Сер. Математика, механика, информатика. — № 3 (42). — (Совм. выпуск. — Ч. 1). — С. 289–294 .
(Отделы вычислительной математики, вычислительных моделей в гидрофизике)
| К началу | |