| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2010 год
Программы фундаментальных исследований Сибирского отделения РАН
- III.19. Общая механика, динамика космических тел, транспортных средств и управляемых аппаратов, биомеханика, механика жидкости, газа и плазмы, неидеальных и многофазных сред, а также механика горения, детонации и взрыва
- IV.29. Системы автоматизации, CALS-технологии, математические модели и методы исследования сложных управляющих систем и процессов
- IV.31. Проблемы создания глобальных и интегрированных информационно-телекоммуникационных систем и сетей. Развитие технологий GRID
- VI.32. Архитектура, системные решения, программное обеспечение и информационная безопасность информационно-вычислительных комплексов и сетей новых поколений. Системное программирование
III.19. Общая механика, динамика космических тел, транспортных средств и управляемых аппаратов, биомеханика, механика жидкости, газа и плазмы, неидеальных и многофазных сред, а также механика горения, детонации и взрыва
Программа III.19.1 Математические проблемы нелинейных моделей движения сложных сред
Координатор программы: академик РАН Л. В. Овсянников
Проект «Моделирование движения жидких сред с поверхностями раздела»№ гос. регистрации 01201056403
Научный руководитель проекта: д.ф.-м.н., проф. В. К. Андреев
Блок 1: Исследование движения и устойчивости в новых моделях конвекции при наличии поверхностей раздела (В. К. Андреев, Ю. В. Гапоненко, И. И. Рыжков).
1. Конфигурация жидкого цилиндрического столбика часто используется и имеет приложение в производстве кристаллов, волокон и мини-струй. Методами численного моделирования проведено комплексное исследование задачи о взаимодействии свободной границы жидкого моста с потоком газа. В качестве жидкости бралось силиконовое масло, а газа — азот. Выявлены характерные структуры течения, их характеристики в зависимости от скорости и направления потока газа, а также температурных условий.
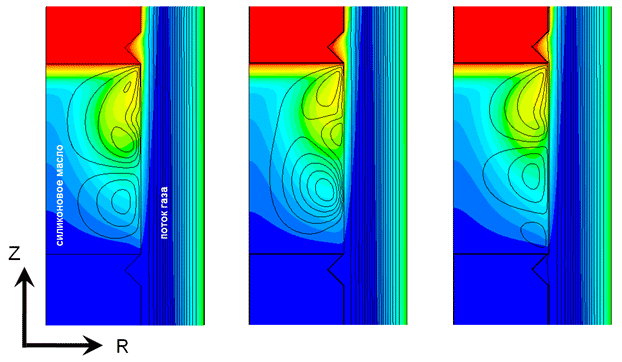
Рис. III.1
На рис. III.1 представлены поле температуры и изолинии функции тока для колебательного режима течения в жидком мосте. Локальное изменение градиента температуры вдоль свободной поверхности приводит к периодическому возникновению областей, где формирование течения вызвано спутным потоком газа.
Определены форма и величина деформации поверхностей жидкого моста, вызванные потоком газа различной интенсивности. На рис. III.2 представлены формы поверхности жидкого моста в зависимости от скорости набегающего потока газа. Видно, что величина деформации свободной поверхности составляет 30-40 мкм для скорости газа 2 м/с, что совпадает с результатами физических экспериментов.
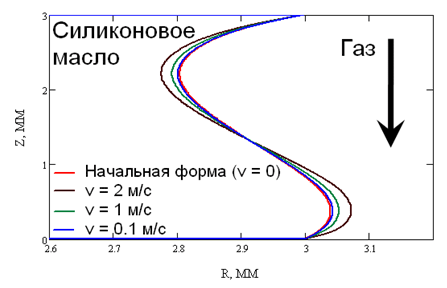
Рис. III.2
2. Исследована задача об устойчивости механического равновесия многокомпонентной смеси в плоском слое, подогреваемом сверху/снизу в поле силы тяжести. Учитываются перекрестная диффузия и эффект Соре. В основном состоянии движение отсутствует, при этом постоянный градиент температуры в слое приводит к возникновению постоянных градиентов концентрации компонентов благодаря эффекту Соре. Рассматриваемая задача является обобщением известной задачи Рэлея — Бенара об устойчивости механического равновесия в плоском слое однородной жидкости, подогреваемой снизу.
С помощью специальных преобразований задача об устойчивости сведена к задаче без перекрестной диффузии и эффекта Соре (исключаются соответствующие члены в уравнениях). Рассмотрено несколько вариантов граничных условий: 1) свободные, проницаемые для вещества границы; 2) твердые, проницаемые для вещества границы; 3) твердые, непроницаемые для вещества границы. Случай проницаемых границ соответствует постоянным значениям концентрации на границах, а случай непроницаемых границ — отсутствию потока вещества через границы. Для граничных условий типа 1 и 2 доказаны теоремы, обобщающие принцип монотонности возмущений (или принцип обращения устойчивости) на случай многокомпонентной смеси с эффектом Соре. Эти теоремы позволяют оценить область устойчивости системы в пространстве параметров. Для граничных условий типа 1 получена явная формула для критических чисел Рэлея.
3. Во многих прикладных задачах свойства среды хорошо описываются моделью идеальной несжимаемой жидкости. Такое положение имеет место при деформировании металлов под действием больших импульсных нагрузок, при взрывах, когда давления настолько велики, что можно пренебречь прочностными и пластическими свойствами среды и силами трения по сравнению с силами инерции. Возникающие при этом нестационарные движения относятся к области гидродинамики со свободными границами, и исследование их устойчивости является чрезвычайно трудной задачей.
Изучена устойчивость совместного нестационарного движения двух несмешивающихся идеальных жидкостей плотности ρ1 и ρ2 соответственно. Основное движение является потенциальным и представляет собой равномерное растяжение плоских слоёв. Скорости в слоях — линейные функции, а давления — нелинейные функции пространственных координат. Свободная граница первой жидкости l1(t) = l10 / (1 + k1t), а второй — l2(t) = l20 / (1 + k2t), где kj > 0 — постоянные; плоскость y = 0 — поверхность раздела жидкостей. При t → ∞ толщины слоев стремятся к нулю. Для задачи о малых возмущениях движения получены априорные оценки. Используя метод лагранжевых координат, удается получить систему амплитудных уравнений для возмущений свободных границ и поверхности раздела с учетом сил поверхностного натяжения. Найдено асимптотическое поведение этих уравнений при t → ∞ и показано, что внешние границы слоев неустойчивы, а поверхность раздела может быть устойчивой. Для конкретных начальных данных и физических параметров приведены зависимости поведения возмущений, полученные численными методами.
4. Рассмотрена задача о совместном однонаправленном движении двух несмешивающихся несжимаемых бинарных смесей с общей границей раздела в условиях невесомости. Предполагалось, что в каждой из смесей имеется растворенное вещество и на поверхности раздела поверхностное натяжение линейно зависит от температуры и концентрации. Движение смесей описывается системой уравнений термодиффузии с граничными условиями на поверхности раздела и твердых стенках. Показано, что если движение возникает под действием термокапиллярных сил, то в системе реализуется стационарное течение типа Куэтта, а температура и концентрация описываются полиномами третьего порядка по поперечной к слоям координате.
Для исследования устойчивости этого течения проведен асимптотический анализ для длинноволновых возмущений при условии недеформируемости поверхности раздела. Оказалось, что бесконечно длинные волны монотонно затухают. Полная спектральная задача решена методом ортогонализации С. К. Годунова, адаптированным для задачи с граничными условиями на твердых стенках и поверхности раздела. Найденные асимптотические значения использовались в качестве начального приближения. Проведенные расчеты показали, что в случае недеформируемости поверхности раздела течение становится более устойчивым с усилением термокапиллярного эффекта на поверхности раздела.
Блок 2: Построение точных решений уравнений движения сложных сред. Нахождение достаточных условий для двух дифференциальных операторов, аннулирующих заданные функции и переводящих решения одного уравнения второго порядка в решения другого уравнения второго порядка (О. В. Капцов, А. А. Родионов, Ю. В. Шанько).
1. Исследованы групповые свойства уравнений термодиффузии. Движение смеси описывается системой
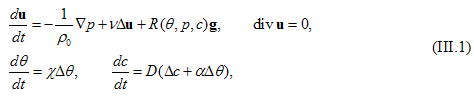
где d / dt = δ / δt + u·∇, u — вектор скорости, p — давление, θ — температура среды, c — концентрация легких компонентов, g = (0,0,−g) — вектор массовых сил, ν — кинематическая вязкость, χ,D,α — коэффициенты температуропроводности, диффузии и Соре, R(θ,p,c) — функция, определяющая силу плавучести. Система уравнений (III.1) дополняется дифференциальными следствиями по x,y,z,t первых четырех уравнений
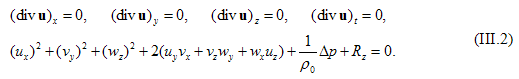
Уравнения (1), (2) находятся в инволюции. Решена задача групповой классификации по функции R(θ,p,c) уравнений (III.1) вместе с (III.2). Получено ядро основной алгебры Ли операторов при произвольном выборе функции и спецификации функции, при которых ядро алгебры Ли расширяется.
2. Рассмотрено кольцо F[δ1,δ2] линейных дифференциальных операторов с коэффициентами из кольца гладких функций F, заданных в области V пространства R2, порожденное двумя дифференцированиями δ1,δ2. Множество операторов, аннулирующих функции u1,...,up, образует левый идеал Ann(u1,...,up). Доказано, что если два оператора L, М (порядков n и m соответственно) аннулируют nm линейно независимых функций u1,...,unm, то они являются образующими левого идеала Ann(u1,...,unm). При этом дополнительно требуется, чтобы характеристические многочлены операторов L, M не имели общих множителей. Показано, что два оператора порядков n и m, характеристические многочлены которых не имеют общих множителей, не могут одновременно аннулировать более nm линейно независимых функций. Если имеется уравнение второго порядка Lu = 0 и даны его 2n решений u1,...,u2n, то можно построить оператор M порядка n, аннулирующий те же функции u1,...,u2n. Оператор M переводит решения уравнения Lu = 0 в решения другого уравнения второго порядка, при выполнении соответствующих условий теоремы. Для гиперболического уравнения второго порядка в каноническом виде подобное утверждение было доказано Дарбу.
Основным результатом является следующее утверждение.
Теорема. Пусть заданы операторы L,M ∈ F[δ1,δ2], порядков n и k соответственно. Предположим, что результант главных символов операторов L, M не равен нулю. Тогда пространство решений системы
Lu = Mu = 0, (III.4)
конечномерно и его размерность не больше nk. Если же размерность пространства <u1,...,unk> решений системы (III.4) равна nk, то
1) операторы L, M являются образующими аннулирующего идеала Ann(u1,...,unk) кольца F[δ1,δ2];
2) операторы L, M замкнуты относительно коммутирования;
3) существуют операторы L1, M1 такие, что выполнено равенство M1L = L1M, причем ord(L1) = ord(L), ord(M1) = ord(M).
Для трехмерных уравнений Эйлера течения идеальной жидкости построены несколько новых классов точных решений. Полученные точные решения имеют произвол в две функции двух переменных. Построены примеры, которые можно интерпретировать как движение частиц жидкости по спиралям, при котором вся жидкость ограничена твердой стенкой, а также как нестационарное движение жидкости, заключенной между двумя свободными границами и твердой стенкой (рис. III.3).

Рис. III.3. Примеры течения. Незамкнутые линии на рисунках являются траекториями движения частиц жидкости вдоль стенок. Остальные траектории имеют ту же форму и получаются из изображенных путем сжатия в направлении оси симметрии
Научная новизна результатов и их значимость. Все полученные результаты являются новыми. Они могут быть использованы для построения решений моделей механики сплошной среды.
Блок 3. Модификация одномерных математических моделей для исследования вертикальной структуры меромектического озера (В. М. Белолипецкий, П. В. Белолипецкий, С. Н. Генова).
Сбор и анализ результатов измерений распределения СО2 в приземном слое атмосферы. Построение одномерной и нульмерной моделей для определения динамики концентраций CO2 над бореальными лесами.
4.1. Вертикальные распределения температуры и солености воды в глубоководной зоне озера в различные сезоны можно определить по одномерной модели, предложенной в работе [Белолипецкий В. М., Генова С. Н. Численное моделирование годовой динамики вертикальной структуры соленого озера // Вычислительные технологии, 2008. — Т.9. — №4. — С. 34-43]. Предполагается, что уровень водной поверхности водоема не меняется. Одномерная модель для периода отсутствия ледяного покрова основывается на решении одномерных в вертикальном направлении уравнений диффузии относительно температуры и солености воды. Коэффициент вертикального турбулентного обмена определяется по формуле Прандтля — Обухова с учетом приближения Экмана. Тепловой поток на водной поверхности вычисляется по известным эмпирическим формулам.
В зимний период по вертикали выделяются: слой льда, слой конвективного перемешивания и придонный слой. Для определения динамики толщины ледяного покрова применяется упрощенная модель, основанная на квазистационарном температурном режиме в затвердевшей области. В соленых озерах при образовании льда в результате кристаллизации воды высвобождается соль. Формируется неустойчивая плотностная стратификация, приводящая к интенсивной вертикальной циркуляции и образованию слоя конвективного перемешивания. В этом слое происходит выравнивание температуры и солености. Уравнение состояния соленой воды принимается в приближении Буссинеска (плотность линейно зависит от температуры и солености воды). Предполагается, что конвективное перемешивание распространяется до такого горизонта, на котором плотность воды становится равной плотности подстилающего слоя воды. На основе этой гипотезы строится численная процедура для определения глубины распространения конвекции и значений температуры, солености, плотности воды в конвективном слое.
Весной температура льда повышается до температуры фазового перехода и происходит таяние ледяного покрова как снизу, так и сверху. После таяния льда образуется слой опресненной воды, который под воздействием ветра перемешивается с нижними слоями воды.
Однако при изменениях уровня водной поверхности озера необходимо учитывать мелководные участки. Выполнена модификация одномерной в вертикальном направлении модели температурного и солевого режимов озера, учитывающая зависимость объема от глубины водоема. В модифицированной одномерной модели для периода отсутствия ледяного покрова вертикальные распределения температуры и солености в озере определяются из уравнения диффузии, осредненного по горизонтальному сечению.
В зимний период толщина слоя конвективного перемешивания определяется с учетом объема замерзшей воды. Изменение солености воды в слое конвективного перемешивания на временном шаге Δt определяется по формуле, учитывающей объем замерзшей воды. Поскольку в зимний период плотностная стратификация под ледяным покровом, в основном, зависит от солености воды, то из предположения, что конвективное перемешивание распространяется до такого горизонта, на котором плотность воды становится равной плотности подстилающего слоя воды, получаются простые расчетные формулы для вычисления заглубления слоя конвективного перемешивания. Зависимость объема от глубины принимается в виде полинома третьей степени.
В летний период при увеличении глубины озера предполагается, что увеличение глубины происходит за счет притока пресной воды. В этом случае средняя соленость в озере уменьшается. Увеличение глубины учитывается добавлением сверху слоя пресной воды толщиной ΔH.
В летний период в случае уменьшения глубины предполагается, что уменьшение глубины связано с превышением испарения над притоком и после испарения вся соль остается в озере. В этом случае средняя соленость в озере возрастает, ( при условии постоянства запасов соли в водоеме). При уменьшении глубины озера на ΔH вычисляется количество соли, выделевшейся при испарении. Эта соль добавляется в поверхностный слой воды и выполняется расчет вертикального распределения солености по алгоритму для летнего периода.
Выполнена серия расчетов динамики вертикальных распределений температуры и солености воды в озере Шира для разных лет. Результаты расчетов хорошо согласуются с данными натурных измерений (рис. III.4). Расчеты показали, что при уменьшении глубины озера слой конвективного перемешивания в зимние периоды может достигать дна.
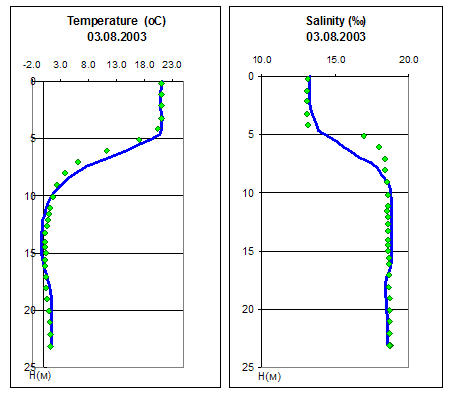
Рис. III.4. Вертикальные профили температуры (°С) и солености (‰) в глубоководной области озера Шира. Сплошная линия — расчеты, точки — натурные измерения
Описанную математическую модель можно применять для оценки динамики вертикальных распределений температуры и солености воды, учитывающей изменение глубины и мелководные участки озера.
4.2. Рассмотрена одномерная модель для описания вертикальных распределений CO2 в приземном слое атмосферы. Для вычисления коэффициента вертикального обмена в приземном слое атмосферы предлагаются соотношения, полученные с использованием формулы Прандтля-Кармана, оценки толщины пограничного слоя и логарифмического закона вертикального распределения скорости ветра.
Предложен метод для определения потока CO2 (QC), использующий точечную модель для концентраций углекислого газа в атмосфере и измеренные на высоких вышках профили концентраций в атмосфере. Показано, что для оценки потока QC достаточны данные измерений концентраций CO2 на уровне вышки. Выполнен анализ данных измерений концентраций CO2 на вышке, взятых с сервера ftp://ftp.cmdl.noaa.gov/ccg/towers/.
Результаты работы были представлены на Международной конференции по измерениям, моделированию и информационным системам для изучения окружающей среды: ENVIROMIS — 2010, г. Томск, 2010 и международной конференции «Лаврентьевские чтения по математике, механике и физике», г. Новосибирск, 2010.
Научная новизна результатов и их значимость. Выполнена модификация одномерной математической модели для исследования вертикальных распределений температуры и солености воды озера в различные сезоны года, учитывающая изменение уровня водной поверхности. Показано, что при уменьшении глубины озера слой конвективного перемешивания зимой может достигать дна и придонные слои окажутся насыщенными кислородом.
Возможность практического применения. Сезонные изменения вертикальных распределений температуры и солености воды необходимо учитывать при математическом моделировании динамики компонентов водной экосистемы.
Блок 4: Разработка теоретических и численных моделей для исследования волн и структур в жидких пленках. Адаптация метода и программы для численного моделирования бегущих уединенных волн (В. Б. Бекежанова, А. М. Франк).
1. Изучено термокапиллярное течение жидкой пленки под воздействием спутного потока газа. Внешними границами такой двухфазной системы являются неподвижные твердые стенки. В жидкости и газе реализуется течение Пуазейля. Для газовой фазы последнее предположение оправданно в силу того, что высота канала (1.4 мм) и скорости течения газа достаточно малы. На деформируемой поверхности раздела выполняются кинематическое, динамическое и энергетическое условия. Построено решение, описывающее стационарное течение и исследована устойчивость полученного решения по отношению к малым возмущениям. Для системы FC-72 — азот обнаружены различные типы неустойчивости. Возникающие неустойчивости могут приводить к образованию различных форм течения (рис. III.5 — III.6).

Рис. III.5. a) картина течения, наблюдаемая в эксперименте (Cheverda and Kabov 2008), b) нейтральные кривые монотонной неустойчивости Ma(k) при g = 0, 1, 2, 3 − Rel = 5,2,1 и характерная форма конвективных ячеек. Области неустойчивости расположены выше нейтральные кривых

Рис. III.6. a) структура течения в эксперименте (Cheverda and Kabov 2008), b) нейтральные кривые Ma(k) при g = 0, 1, 4 − Reg = 200, 2, 5 − Reg = 300, 3, 6 − Reg = 400. Штриховыми линиями показаны кривые колебательной неустойчивости, сплошными — монотонной
Появление продольных валов обусловлено термокапиллярным эффектом. Для больших значений чисел Rel и Reg наблюдается сосуществование продольных полос, порожденных силами Марангони, и поперечных гидротепловых волн, которые распространяются на поверхности под углом к основному течению в противоположном потоку направлению. Для данных режимов течений существенно влияние микрогравитации и расходных чисел Рейнольдса.
2. Разработана и реализована программа для расчета трехмерных уединенных волн в тонкой жидкой пленке, стекающей по вертикальной поверхности под действием силы тяжести. Применен метод частиц с базисными функциями в виде декартового произведения сплайнов и полиномов. Для адекватного моделирования течения в «бесконечной области» используется расчетная область, движущаяся вслед за волной. На передней (входной) границе задается невозмущенный поток, на задней — специфические для данного метода «мягкие» условия, которые можно интерпретировать как перенос величин к границе по характеристикам в совокупности с нулевым диффузионным потоком через границу. На боковых границах области используются условия периодичности. Осложняющим обстоятельством здесь является то, что расчетная область вслед за волной движется по течению пленки с заранее неизвестной скоростью, которая определяется в процессе решения. Поэтому уравнения решаются в исходной неподвижной системе координат, вследствие чего среднее течение пленки на «выходной» границе области направлено внутрь, что может приводить к некорректности «мягких» граничных условий. Расчеты показали, что задача корректна, если область движется немного быстрее пленки, что всегда выполнено в случае задачи об уединенных волнах.
Научная новизна результатов и их значимость. Подковообразные трехмерные капиллярно-гравитационные волны, близкие по поведению к уединенным, долгое время наблюдались в экспериментах лишь как часть (фрагмент) некоторой хаотической трехмерной структуры, которую иногда называют поверхностной турбулентностью. Недавно такие волны были целенаправленно получены и изучены при небольших числах Рейнольдса в экспериментах Алексеенко и др. (2005). Теоретический солитон в пленке был впервые получен Петвиашвили и Цвелодубом (1978) как решение некоторого приближенного уравнения движения пленки, а позднее также в работах Демехина, Каллиадасиса и др. в рамках приближенных уравнений погранслоя (модель Шкадова). Солитоны, как решения полных уравнений Навье-Стокса ранее получены не были.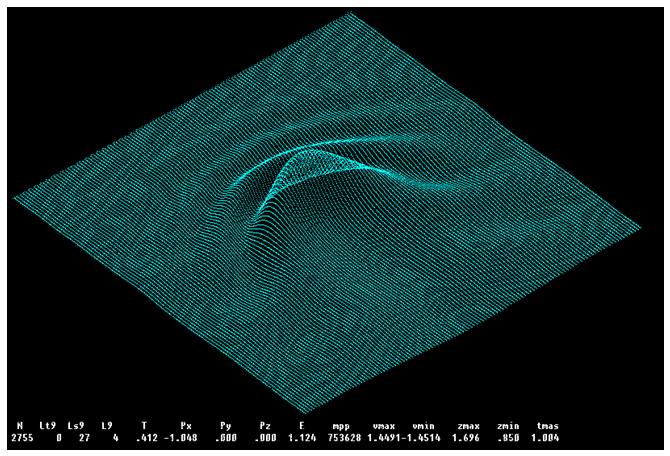
Рис. III.7. Солитон при числе Рейнольдса пленки Re=3.9
Важнейшие публикации:
К блоку 1:
- Gaponenko Yu., Glockner S., Shevtsova V.
Control of thermocapillary interface by gas flow in liquid bridges // MultiFlow — 2010, Brussels, Belgium. — 2010. — [электронный ресурс]. - Андреев В. К.
Неустойчивость совместного движения плоских слоев идеальной жидкости // Тез. докл. междунар. конф. «Лаврентьевские чтения по математике, механике и физике». — Новосибирск. — 2010. — С. 60. - Андреев В. К., Бекежанова В. Б.
Устойчивость неизотермических жидкостей. — Красноярск: СФУ. — 2010. — ISBN:978-5-7638–203 1-7. — 356 с. - Ryzhkov I. I., Gaponenko Y. A.
On the Boussinesq approximation in the problems of convection induced by high frequency vibration // J. of Siberian Federal University: Mathematics & Physics. — 2010. — № 3(4). — P. 433–449 . - Gaponenko Y., Miadlin A., Shevtsova V.
Liquid entrainment by gas flow along the interface // Book of Abstracts the 5th Conf. of the Intern. Marangoni Association «International Fluid Dynamics and Process». — Florence, Italy. — P. 44-49. - Ryzhkov I. I.
Thermocapillary instabilities in liquid columns under co- and counter-current gas flow // J. Physics of Fluids, 2010 (принята в печать).
К блоку 2:
- Родионов А. А., Краснова Д. А.
Групповые свойства одной модели термодиффузии с уравнениями в инволюции // Тез. докл. междунар. конф. «Лаврентьевские чтения по математике, механике и физике». — Новосибирск. — 2010. — С. 35-36. - Капцов О. В.
Идеалы дифференциальных операторов и преобразования линейных уравнений с частными производными // Программирование. — 2010. — Т. 36. — № 2. — С.97–102 . - Капцов О. В.
Методы интегрирования уравнений с частными производными. М.: Физматлит. — 2009. - Шанько Ю. В.
О некоторых точных решениях трехмерных уравнений идеальной жидкости // Вычислительные технологии. — 2010. — Т. 15. — № 5. — С. 123–130 .
К блоку 3:
- Belolipetskii V. M., Belolipetskii P. V.
Numerical algorithm for studying wind flows two-dimensional in the in vertical plane in stratified reservoirs // Russ. J. Numer. Anal. Math. Modelling. — V. 25. — № 1. — P. 1-14. - Belolipetskii P. V., Belolipetskii V. M., Genova S. N., Mooij W. M.
Numerical modeling of vertical stratification of Lake Shira in summer // Aquat Ecol. — V. 44. — P. 561–570 . - Rogozin D. Y., Genova S. N., Gulati R. D., Degermendszhi A. G.
Some generalizations based on stratification and vertical mixing in meromictic Lake Shira, Russia, in the period 2002–200 9 // Aquat Ecol. — V. 44. — P. 485–496 . - Genova S. N., Belolipetskii V. M., Rogozin D. Y., Degermendszhi A. G.
A one-dimensional model of vertical stratification of Lake Shira focussed on winter conditions and ice cover // Aquat Ecol. — V. 44. — P. 571–584 . - Mooij W. M., Belolipetskii P. V., Genova S. N. et al.
Challenges and opportunities for integrating lake ecosystem modelling approaches // Aquat Ecol. — V. 44. — P. 633–667 .
К блоку 5:
- Некрасова Т. И., Франк А. М.
Дисперсия линейных волн в методе частиц для несжимаемой жидкости // Вычислительные методы и программирование. — 2010. — Т. 11. — С. 228–233 .
(Отделы Дифференциальных уравнений механики, Вычислительных моделей в гидрофизике)
| К началу | |