| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2010 год
Программы фундаментальных исследований Сибирского отделения РАН
- III.19. Общая механика, динамика космических тел, транспортных средств и управляемых аппаратов, биомеханика, механика жидкости, газа и плазмы, неидеальных и многофазных сред, а также механика горения, детонации и взрыва
- IV.29. Системы автоматизации, CALS-технологии, математические модели и методы исследования сложных управляющих систем и процессов
- IV.31. Проблемы создания глобальных и интегрированных информационно-телекоммуникационных систем и сетей. Развитие технологий GRID
- VI.32. Архитектура, системные решения, программное обеспечение и информационная безопасность информационно-вычислительных комплексов и сетей новых поколений. Системное программирование
IV.29. Системы автоматизации, CALS-технологии, математические модели и методы исследования сложных управляющих систем и процессов
Программа IV.29.1 Теоретические основы и методы информационных и вычислительных технологий проектирования и принятия решений
Координаторы программы: академик РАН Ю. И. Шокин, член-корреспондент РАН В. В. Шайдуров
Проект IV.29.1.2 «Информационно-вычислительные технологии для анализа и проектирования сложных систем в ближнем космосе»№ гос. регистрации 01201056404
Научный руководитель проекта: член-корреспондент РАН В. В. Шайдуров
Блок 1. Создание трехмерной стационарной модели электропроводности атмосферы (В. В. Денисенко)
Создана трехмерная стационарная модель электропроводности атмосферы, которая основана на минимизации функционала энергии, квадратичная часть которого равна Джоулевой диссипации. Модель реализована в виде комплекса программ на языке Фортран. Проанализированы электрические поля и токи, проникающие из ионосферы через атмосферу до поверхности Земли. Показано, что вблизи поверхности Земли как следствие разности потенциалов в ионосферной полярной шапке могут наблюдаться изменения вертикального электрического поля до 50 В/м, если пункт наблюдения находится в высоких широтах.
Предложена математическая модель для описания квазистационарных атмосферных электрических полей с приближенным, но достаточно точным учетом проводимости ионосферы. Показано, что известные модели проникновения электрического поля от поверхности Земли в ионосферу приходится считать неудовлетворительными, хотя в атмосфере ниже 50 км они дают хорошие результаты. В этих моделях за счет произвольной постановки граничного условия на верхней границе атмосферы фактически исключен существующий хороший проводник или, наоборот, добавлен несуществующий. Максимально возможное поле в нашей модели получилось намного меньшим, чем в моделях, в которых ионосферная проводимость не учитывалась, но намного большим, чем в моделях, основанных на приближении с бесконечной Педерсеновской проводимостью в верхней ионосфере.
Особенный интерес к проникновению поля в ионосферу связан с высказанным примерно десять лет назад предложением использовать для выявления предвестников землетрясений измерения электрического поля со спутников, летающих на небольших высотах, вместо того, чтобы создавать плотную сеть наземных станций, измеряющих вариации электрического поля непосредственно в приземном слое атмосферы. Такое предложение базировалось на результатах модели, предсказывавшей достаточно сильное проникновение электрического поля из нижней атмосферы в ионосферу. Наше моделирование показало, что выделение проникающих полей, к сожалению, невозможно, поскольку их напряженность на несколько порядков меньше, чем напряженность обычно существующих в ионосфере полей иной природы.
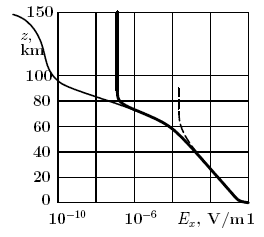
Рис. III.8. Высотные распределения горизонтальной компоненты электрического поля, проникающего от поверхности Земли в ионосферу, полученные в результате расчетов в рамках трех моделей. Наша модель — жирная кривая; модель, не учитывающая проводимость ионосферы, — штриховая кривая; модель, базирующаяся на бесконечной Педерсеновской проводимости F-слоя ионосферы, — тонкая кривая
Блок 2. Математическое моделирование электромагнитных явлений в атмосфере и ионосфере (Н. В. Еркаев)
Совместно с Институтом космических исследований Австрийской академии наук получены результаты численного магнитогидродинамического моделирования нелинейной стадии неустойчивости Кельвина-Гельмгольца в ионосфере планет. Начальные возмущения задавались на фоне одномерных равновесных профилей скорости, плотности, давления и магнитного поля. На основе численного решения начально-краевой задачи для идеальных уравнений магнитогидродинамики выделены три стадии развития волн Кельвина-Гельмгольца, в том числе нелинейные (рис. III.9, III.10).
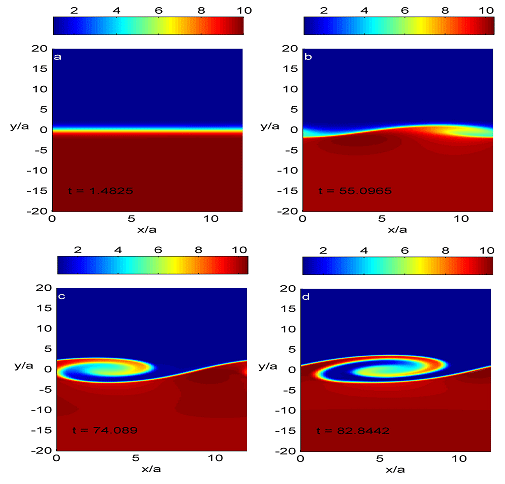
Рис. III.9. Распределение плотности на различных стадиях развития неустойчивости Кельвина-Гельмгольца: a — начальное состояние; b — линейная стадия; c и d — нелинейная стадия
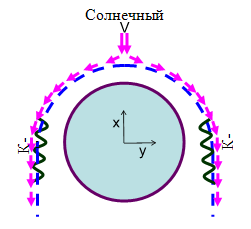
Рис. III.10. Область неустойчивости в случае обтекания солнечным ветром ионосферы планеты, не имеющей собственного магнитного поля. Обтекаемая граница показана штриховой линией
Блок 3. Разработка математической модели теплового режима приборного блока космического аппарата на основе сотопанели, содержащей тепловые трубы, гипертеплопроводящие пластины и электрические нагреватели» (В. А. Деревянко, Е. Н. Васильев, А. В. Макуха, С. В. Кукушкин).
Разработана математическая модель процессов теплообмена в объеме сотовой панели. Модель базируется на численном решении системы нестационарных уравнений теплопроводности. Проведены вычислительные эксперименты по исследованию пространственной неоднородности температурных полей и временной нестабильности температуры в различных условиях работы. На основе математической модели создан пакет прикладных программ, предназначенный для теплового проектирования приборных блоков космических аппаратов.
Вычислительные эксперименты показали, что рассматриваемая конструкция и алгоритм работы БСТ обеспечивают заданную стабильность поддержания температуры ±0.01 °С. Результаты математического моделирования были учтены при разработке требований к конструкции БСТ и выработке алгоритмов режимов работы.
Работа выполнена в интересах ОАО «Информационные спутниковые системы им. ак. М. Ф. Решетнева», г. Железногорск.
Блок 4. Применение нанотехнологий для повышения качества металлоизделий (Г. Г. Крушенко).
В области структурирования металлических расплавов с помощью нанотехнологий активно применяется процесс модифицирования — введение в металлические жидкие сплавы компонентов, которые в процессе растворения образуют с основой сплава тугоплавкие химические соединения наноразмерного диапазона, служащие центрами кристаллизации. В результате модифицирования литые изделия приобретают мелкокристаллическую структуру, что приводит к повышению уровня механических свойств и эксплуатационных характеристик деталей.
В индукционной печи типа МГП52А по стандартной технологии готовился алюминиево-кремниевый сплав АК12 (10.5% Si; 0.8% Fe; 0.3% Mn; остальное — Al). После доведения температуры расплава до 750 С производили его переливание в равных частях в графито-шамотовые тигли, установленные в двух электрических печах сопротивления, в одном из которых температуру расплава доводили до 8
Блок 5. Дисперсионное упрочнение алюминиевых сплавов при полунепрерывном литье слитков (Г. Г. Крушенко).
В работе достигнуто дисперсионное упрочнение алюминиевых сплавов наночастицами оксида алюминия Al2O3 при литье слитков полунепрерывным способом. Поставленная цель достигается введением наночастиц оксида алюминия Al2O3 в лунку кристаллизатора в объеме прутка, отпрессованного из гранул одноименного сплава. В обычных условиях алюминий покрыт тонкой окисной пленкой α-Al2O3 толщиной 10−5 мм с высокой температурой плавления и высокой твердостью. При прессовании контейнера с гранулами в фильере пресса возникают значительные усилия, что приводит к значительному раздроблению хрупкой окисной пленки на дисперсные частицы, которые и обеспечивают упрочнение сплава по механизму дисперсионного упрочнения. Кроме того, они могут служить дополнительными центрами кристаллизации.
Работа выполнена при литье полунепрерывным способом слитков Ø 120 мм из алюминиевого деформируемого сплава дуралюмин Д1. Гранулы размером 1.5-3.0 мм получали методом центробежной разливки. Прутки диаметром 9.5 мм изготовляли путем прессования тонкостенного цилиндрического контейнера, предварительно нагретого до 6
Разработана новая промышленная технология изготовления алюминиевых композитов (Рис. III.11) в виде профилей протяженной длины (метры) любого сечения (уголок, швеллер, трубки и др.) путем экструзии композиции, состоящей из частиц алюминия или деформируемых алюминиевых сплавов (например, гранулы) и высокопрочных нанопорошков химических соединений (нитриды, карбонитриды, оксиды, карбиды и др.). Композиты обладают более высокими механическими свойствами и усталостными характеристиками по сравнению с профилями, отпрессованными из компактной заготовки.
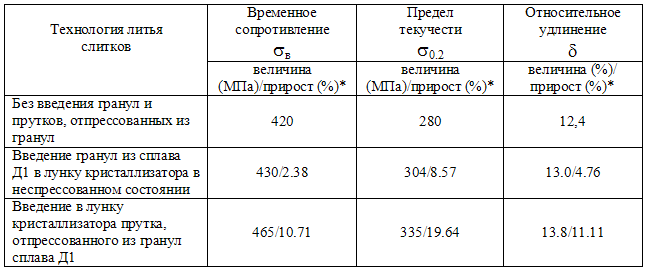
Таблица III.1. Механические свойства прутков Ø 16 мм, отпрессованных из слитков Ø 120 мм, отлитых из сплава Д1 в зависимости от технологии литья слитков
(* прирост свойств относительно «безгранульной» технологии литья слитков)

Рис. III.11. Профили, отпрессованные из гранул деформируемых алюминиевых сплавов и нанопорошков (длина горизонтальной полочки крайнего слева уголка равна 70 мм)
Блок 6. Компьютерная модель глубинной геодинамики (В. В. Шайдуров, Г. И. Щепановская, М. В. Якубович, А. В. Вяткин).
Исследование направлено на разработку математической модели, описывающей состояние плотности, динамической вязкости, внутренней энергии и высоких температур структуры Земли. Предлагается компьютерная модель, позволяющая рассмотреть геодинамические процессы расширения, сжатия, разогревания и охлаждения Земли на геологических периодах времени. Динамика геосфер исследуется в рамках модели сферически-симметричной вязкой теплопроводной сжимаемой среды, когда четыре упомянутых величины меняются по глубине и по времени. Настоящая модель по глубине содержит кору и мантию Земли, внешнее и внутреннее ядро.
На основе метода конечных элементов получена консервативная вариационно-разностная схема первого порядка аппроксимации по времени и глубине. Рассмотрены различные варианты прямых и итерационных методов решения квазилинейных сеточных уравнений. Описанные алгоритмы реализованы на языке C++. Вычислительный эксперимент продемонстрировал устойчивость и сходимость построенного алгоритма при измельчении параметров дискретизации по времени и глубине. Вместе с тем, построенная вычислительная модель проявила значительную чувствительность к уравнению состояния.
В рамках полученной компьютерной модели рассмотрены варианты динамики геосфер при некоторых уравнениях состояния. В качестве начальных условий использованы значения, взятые из научной литературы, где они определены как эмпирически, так и на основании экстраполяции физических законов. Распределение плотности вещества Земли, как следует из экспериментальных данных, соответствует скачкообразному изменению плотности при переходе через границы Мохоровичича и Вихерта-Гутенберга. На рис. III.12 представлено распределение скорости в различные моменты времени при одном из уравнений состояния; поведение кривых отражает движение вещества от ядра к мантии и от мантии к коре.
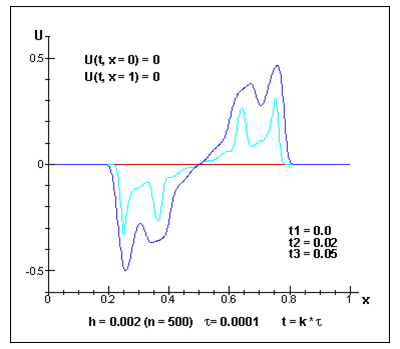
Рис. III.12. Распределение скорости перемещения вещества вдоль радиуса Земли в различные моменты времени
Традиционно считается, что с успехом можно использовать линеаризованные модели, учитывая довольно медленные осреднённые перемещения вещества внутри Земли. Однако в нашей модели уравнения состояния содержат как условия метаморфизма вещества, так и его фазовых переходов. Эти условия при мощном гравитационном воздействии, в принципе, могут привести к более быстрому изменению состава и объема геосфер, чем при механическом перемещении с учетом медленного остывания. Так что модель будет полезна для анализа возможных прошлых и будущих более быстрых изменений геосфер.
Блок 7. Динамика лазерного охлаждения ионов и их структуризация в разреженной плазме (А. П. Гаврилюк).
Исследование динамики лазерного охлаждения ионов и их структуризация в разреженной плазме проведено с использованием метода броуновской динамики.
В частности, из полученных результатов следует, что оптимальный по времени режим достижения конечного упорядоченного состояния ионной подсистемы может заключаться в использовании нескольких последовательных лазерных импульсов, в промежутках между которыми успевает происходить быстрая частичная «кристаллизация» плазмы (рис. III.13). При концентрации плазмы ≤ 108см−3 было обнаружено также возникновение неравновесного распределения кинетической энергии по поступательным степеням свободы ионов при их одномерном охлаждении.
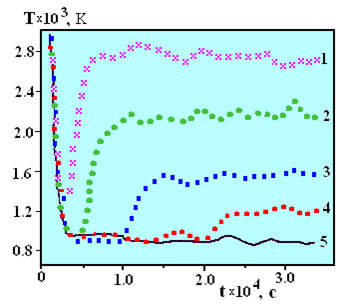
Рис. III.13. Значения температур ионов, устанавливающиеся в результате их корелляционного нагрева после действия импульса лазерного охлаждающего излучения длительностью: 1 — 3·10−5 с, 2 — 5·10−5 с, 3 — 1·10−4 с, 4 — 2·10−4 с, 5 — 5·10−4 с. Концентрация частиц n = 106 см−3, частота Раби |V0| = 0.2γ, отстройка от резонанса (в «красную» область) Δ = 0.39γ
Блок 8. Математическая модель механического действия полихроматического света на атомы (ионы) с триподной конфигурацией атомных переходов (И. В. Краснов).
В рамках формализма квазиклассической матрицы плотности в представлении Вигнера построена математическая модель механического действия полихроматического света на атомы (ионы) с триподной конфигурацией атомных переходов, т.е. переходов вида F=1-F=0, где F — полный угловой момент атомного состояния. Получено уравнение Фоккера-Планка для вигнеровской функции распределения таких атомов, позволяющее моделировать их движение в полихроматическом поле специальной пространственной конфигурации. На основе анализа решений этого уравнения впервые продемонстрирована возможность длительной трехмерной локализации (в сверхглубоких потенциальных ямах) и субдопплеровского охлаждения атомов с триподной конфигурацией переходов посредством воздействия выпрямленных градиентных сил. Рассмотренная диссипативная оптическая ловушка для атомов не требует использования неоднородного магнитного поля как в широко используемых магнито-оптических ловушках. Показано, что параметры такой чисто оптической ловушки можно изменять в широком диапазоне значений посредством вариации интенсивностей полей и перестройки геометрических параметров: углов пересечения интерферирующих световых пучков.
Это позволяет осуществлять непрерывный переход от супердопплеровских состояний атомов к субдопплеровским состояниям без нарушения условий устойчивости локализации (рис. III.14).
Важнейшие публикации:
К блоку 1:
- Денисенко В. В., Помозов Е. В.
Расчет глобальных электрических полей в земной атмосфере // Вычислительные технологии. — Т. 15. — № 5. — С. 34-50. - Ampferer M., Denisenko V. V., Hausleitner W., Krauss S., Stangl G., Boudjada M. Y., Biernat H. K.
Decrease of the electric field penetration into the ionosphere due to low conductivity at the near ground atmospheric layer // Annales Geophysicae. — V. 28. — № 3. — P. 779–787 .
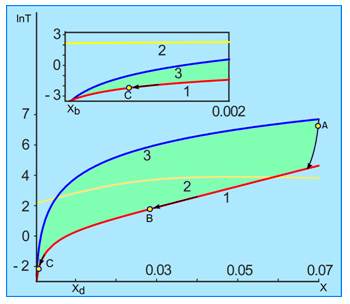
Рис. III.14. Непрерывный устойчивый переход от супердопплеровского нелокализованного состояния атомов (точка A на плоскости X − ln(T)) в субдопплеровское локализованное состояние (точка С) через промежуточные локализованные состояния B при адиабатически медленном изменении безразмерной интенсивности резонансного оптического поля X: T-относительная температура атомов (в единицах допплеровского предела охлаждения — 10−3 K для данного примера); кривая 1 соответствует долгоживущим локализованным состояниям с временем жизни не менее 300 c; кривая 3 — граница области устойчивой локализации атомов (выделенной зеленым цветом); кривая 2 — зависимость степени локализации атомов от X. Переход A − B − С соответствует изменению температуры атомов от 1K до нескольких десятков μK
К блоку 2:
- Erkaev N. V., Semenov V. S., Biernat H. K.
Hall magnetohydrodynamic effects for current sheet flapping oscillations related to the magnetic double gradient mechanism // Physics of Plasmas. — V. 17. — P. 60703. - Amerstorfer U., Erkaev N. V., Taubenschuss U., Biernat H. K.
Influence of a density increase on the evolution of the Kelvin-Helmholtz instability and vortices // Physics of Plasmas. — V. 7. — P. 072901-8. - Taubenschuss U., Erkaev N. V., Biernat H. K., Farrugia C. J., Mostl C., Amerstorfer U. V.
The role of magnetic handedness in magnetic cloud propagation // Annales Geophysicae. — V. 28. — P. 1075–110 0. - Rubab N., Erkaev N. V., Langmayr D., Biernat H. K.
Kinetic Alfven wave instability in a Lorentzian dusty magnetoplasma // Physics of Plasmas. — V. 17. — P. 103704.
К блоку 3:
- Васильев Е. Н., Деревянко В. В.
Математическая модель процессов теплообмена в сотовой панели с тепловыми трубами // Вестник СибГАУ. — 2010. — № 2. — С. 4-7. - Научно-технический отчет «Разработка математической модели теплового режима модуля специальных нагрузок», этап 9.1. — 2010. — 35 с.
- Научно-технический отчет «Разработка математической модели бортового стандарта температуры», этап 9.2. — 2010. — 30 с.
К блокам 4-5:
- Крушенко Г. Г.
Модифицирование алюминиево-кремниевых сплавов никелем и кобальтом // Ремонт. Восстановление. Модернизация. — 2010. — Т. 8. — № 2. — С. 41-43. - Кашубский А. Н., Крушенко Г. Г.
Применение неразрушающих методов для контроля качества и исправления дефектов металлопродукции ответственного назначени // Тяжелое машиностроение. — 2010. — № 3. — С. 13-16. - Краев В. В., Крушенко Г. Г.
Pасчет пpипусков на механическую обpаботку с учетом технологической наследственности // Технология металлов. — 2010. — № 4. — С. 38-41. - Крушенко Г. Г., Фильков М. Н.
Использование нанопорошков химических соединений для изготовления алюминиевых профилей с волокнистой структурой // Конструкции из композиционных материалов. — 2010. — № 3. — С. 8-12. - Степанов В. В. Крушенко Г. Г.
Мониторинг состояния трубопровода высокого давления теплоэлектростанции с целью повышения надежности его эксплуатации. I // Ремонт, восстановление, модернизация. — 2010. — № 10. — С. 28-33. - Степанов В. В. Крушенко Г. Г.
Мониторинг состояния трубопровода высокого давления теплоэлектростанции с целью повышения надежности его эксплуатации. II. // Ремонт, восстановление, модернизация. — 2010. — № 11. — С. 21-25. - Степанов В. В. Крушенко Г. Г.
Оптимизация сроков техни-ческого обслу-живания трубо-проводов высо-кого давления на тепловых электростан-циях // Ремонт, восстановление, модернизация. — 2010. — № 12. — С. 11-16. - Крушенко Г. Г.
Некоторые экспресс-способы определения качества литейных алюминиево-кремниевых и алюминиево-магниевых сплавов // Технология металлов. — 2010. — № 9. — С. 44-47. - Крушенко Г. Г., Фильков М. Н.
Предотвращение образования пригара на стальных и чугунных отливках при окраске форм и стержней красками, содержащими нанопорошки тугоплавких химических соединений // Экология промышленного производства. — 2010. — № 4. — С. 43-46.
К блоку 6:
- Vyatkin A. V., Shaidurov V. V., Shchepanovskaya G. I.
Numerical Spherically-Symmetric Simulation of Deep-Seated Geodynamics // J. of Applied and Industrial Mathematics. — 2010. V. 4. — № 2. — P. 290–297 .
К блоку 7:
- Карпов С. И., Исаев И. Л., Гаврилюк А. П., Грачев А. С., Герасимов В. С.
Кристаллические и фрактальные структуры в наноколлоидах и их приложение в нанофотонике в книге «Фотонные кристаллы и нанокомпозиты: структурообразование, оптические и диэлектрические свойства». — Новосибирск: СО РАН. — 2009. — Вып. 21. — ISBN:978-5-7692–109 6-9. — 257 с. - Krasnov I. V.
Optical cooling and trapping of tripod-type atoms with rectified radiation forces, arXiv: 1009.3118v1, (Cornell University Library). — 2010. — Р. 1-15.
К блоку 8:
- Gavrilyuk A. P., Karpov S. V.
Dynamic changes of optical characteristics of resonant domains in metal nanoparticle aggregates under pulsed laser fields // Applied Physics B: Lasers and Optics. — V. 101. — doi: 10.1007/s00340–010 -4180-x.
(Отделы Вычислительной математики, Вычислительной физики)
| К началу | |