| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2010 год
Программы фундаментальных исследований Сибирского отделения РАН
- III.19. Общая механика, динамика космических тел, транспортных средств и управляемых аппаратов, биомеханика, механика жидкости, газа и плазмы, неидеальных и многофазных сред, а также механика горения, детонации и взрыва
- IV.29. Системы автоматизации, CALS-технологии, математические модели и методы исследования сложных управляющих систем и процессов
- IV.31. Проблемы создания глобальных и интегрированных информационно-телекоммуникационных систем и сетей. Развитие технологий GRID
- VI.32. Архитектура, системные решения, программное обеспечение и информационная безопасность информационно-вычислительных комплексов и сетей новых поколений. Системное программирование
VI.32. Архитектура, системные решения, программное обеспечение и информационная безопасность информационно-вычислительных комплексов и сетей новых поколений. Системное программирование
Программа IV.32.1 Архитектура, информационная безопасность, системные решения и программное обеспечение информационно-вычислительных систем новых поколений
Координаторы программы: член-корреспондент РАН В. Г. Хорошевский, член-корреспондент РАН В. В. Шайдуров
Проект IV.32.1.4 «Анализ сложных математических моделей на суперкомпьютерах с параллельной архитектурой»№ гос. регистрации 01201056402
Научный руководитель проекта: д.ф.-м.н., проф. В. М. Садовский
Блок 1. Техническое сопровождение исследований (С. В. Исаев, А. В. Малышев).
В течение 2010 года выполнена серия работ по оптимизации системы загрузки вычислительного комплекса Института на основе модели гетерогенного вычислительного кластера. Были решены задачи повышения производительности кластера, снижения энергопотребления и минимизации общего времени вычисления набора задач.
В настоящее время кластер МВС-1000/96 состоит из 48 вычислительных узлов, предоставляющих 96 логических процессоров (узлы 1-24 содержат одноядерные, узлы 25-36 — двухядерные процессоры, узлы 37-48 содержат по два двухядерных процессора). Имеется сервер хранения данных Hewlett-Packard HP Proliant DL320s 6TB SATA Storage Server и управляющий узел Athlon 64 3500 2 Гб ОЗУ. Объем ОЗУ — 1 Гб на логический процессор. Установлена сеть передачи данных Gigabit Ethernet, коммуникационная библиотека MPICH2 v.1.0.7. Кластер доступен для пользователей по адресу cluster2.krasn.ru, по протоколам ssh2 и ftp. Доступ в пределах научно-образовательной сети г. Красноярска осуществляется по оптоволоконным линиям связи со скоростью 1000 Мбит/сек, доступ из внешнего мира — по каналу сети СО РАН со скоростью 40 Мбит/сек. Производительность кластера по LINPACK составляет 300 Гфлопс (ранее было 134). Пиковая производительность — 450.8 Гфлопс.
Имеющаяся система запуска задач в первую очередь распределяет ядра из узлов с меньшими порядковыми номерами. Поскольку энергопотребление четырехядерных узлов примерно в полтора раза меньше, чем одноядерных, то для оптимизации его узлы были перенумерованы в порядке уменьшения производительности и энергоэффективности. Это позволило существенно снизить суммарное время выполнения задач. Снижение энергопотребления достигается также за счет отключения незадействованных узлов. В дальнейшем с целью оптимизации предполагается реализовать индивидуальную процедуру запуска, в которой будет учитываться полезность решения данной задачи на основе имеющейся статистики запуска.
Блок 2. Моделирование деформации материалов со сложными реологическими свойствами (В. М. Садовский, М. В. Варыгина, О. В. Садовская).
По научной тематике проекта были продолжены исследования в области разработки параллельных алгоритмов и программ для численного моделирования деформации материалов со сложными реологическими свойствами. К материалам такого рода относятся пенистые металлы — современные высокопрочные материалы на основе алюминия, меди или никеля, пористость которых достигает 75 % и более высоких значений. Согласно информации, опубликованной в Интернете, в 2010 г. профессор А. Рабиней из университета штата Северной Каролины (США) открыла самую прочную пену в мире. Высокая прочность достигается за счет того, что на поверхности тонких прослоек в пене практически отсутствуют дислокации — дефекты, являющиеся зародышами разрушений. Исключительно важным свойством таких материалов является высокий уровень пластической диссипации энергии. Поэтому планируется использовать металлические пены при производстве демпфирующих элементов в машиностроении (бамперов машин) и оборонной промышленности.
На основе предложенного ранее общего подхода к конструированию определяющих соотношений с учетом различного сопротивления материала растяжению и сжатию построена математическая модель пенометалла, описывающая стадию упругого (или упругопластического) деформирования до момента схлопывания пор и стадию пластического течения после схлопывания пор под действием динамических нагрузок. Реологическая схема предлагаемой модели и типичная диаграмма одноосного растяжения-сжатия приведена на рис. III.16.
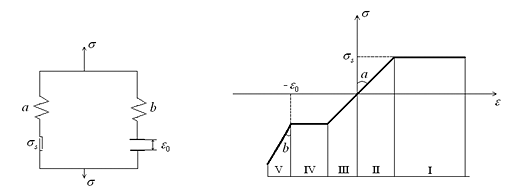
Рис. III.16. Реологическая схема пенистого металла (a — модуль упругости скелета до схлопывания пор, b — модуль упругости металла после схлопывания пор, σs — предел текучести, ε0 — пористость) и диаграмма одноосного деформирования (I — пластическое растяжение скелета, II — упругое растяжение, III — упругое сжатие, IV — пластическое сжатие до момента схлопывания пор, V — деформирование после схлопывания)
Известную проблему составляет вычисление феноменологических констант пенистого металла (модулей упругости, предела текучести) в зависимости от величины пористости. К решению этой проблемы применена технология, основанная на расчете серии статических задач для ячеек периодичности, содержащих определенное число пор.
Разработан алгоритм численной реализации модели динамического деформирования пенистого металла на многопроцессорных вычислительных системах кластерного типа. Параллельная версия программ, исполняющих этот алгоритм, включена в разрабатываемый в рамках проекта программный комплекс. Начаты работы по тестированию и верификации программ на модельных задачах. Планируется выполнить серию расчетов, целью которых является моделирование и оптимизация демпфирующих свойств пространственных элементов конструкций из пенистых металлов.
Блок 3. Моделирование распространения гравитационных волн в больших акваториях (Е. Д. Карепова, А. В. Малышев, Е. В. Дементьева).
По тематике, связанной с разработкой и исследованием математических моделей распространения гравитационных волн в морских акваториях, выполнен анализ параллельных реализаций метода конечных элементов для численного решения начально-краевой задачи для уравнений мелкой воды. В частности, сопоставлена эффективность двух широко распространенных реализаций стандарта MPI, исследовано поведение разработанного программного обеспечения при использовании различных способов выделения памяти, а также обнаружено несколько интересных эффектов, возникающих при измерении и оценке затрат на обмен данными между вычислительными процессами.
Численное моделирование поверхностных волн в больших акваториях проводилось с учетом сферичности Земли и ускорения Кориолиса на основе системы уравнений мелкой воды. Для этой задачи был построен метод конечных элементов, который приводит к системе линейных алгебраических уравнений. Полученная система решается итерационным методом Якоби, обладающим хорошим параллелизмом. Диагональное преобладание для его сходимости обеспечивается выбором шага по времени. Рассмотрены различные способы реализации параллельного вычислительного процесса — декомпозиция с выделением теневых граней, когда область решения задачи включает взаимно перекрывающиеся подобласти (ширина перекрытия определяется шаблоном дискретного аналога), и декомпозиция без выделения теневых граней, когда исходная область разрезается на подобласти, пересекающиеся только по границам разреза. Для каждой граничной точки во втором способе невязка насчитывается частично только по тем элементам, которые лежат в рассматриваемой подобласти. При обмене данными после каждой итерации Якоби требуется дополнительное суммирование для значений невязки в граничных точках.
В результате сравнительных расчетов было установлено, что наиболее эффективным оказывается алгоритм декомпозиции без теневых граней с реализацией двухточечных обменов в неблокирующем режиме. Были также рассмотрены теоретические оценки ускорения параллельного алгоритма, которые согласуются с ускорением, полученным в расчетах. Численные эксперименты показали хорошую масштабируемость параллельной реализации программ.
Проведена серия численных экспериментов, целью которых было сравнение производительности двух популярных реализаций MPI — MPICH2 v.1.2.1p1 и OpenMPI v.1.4.1. Расчеты показали чувствительность времени выполнения алгоритма к способу выделения памяти. Статическое распределение памяти дает преимущество в обеих реализациях MPI. Использование динамического распределения памяти в алгоритмах такого рода требует дополнительного уточнения стратегии выделения памяти при компиляции (рис III.17).
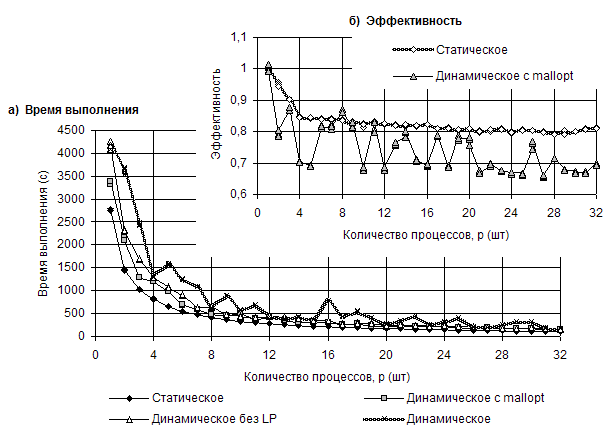
Рис. III.17. Графики зависимости времени выполнения (а) и эффективности (б) от количества процессов для различных стратегий работы с памятью
Лучший результат при использовании динамического выделения памяти показал пакет MPICH2 с уточнением стратегии выделения памяти mallopt(), отключающий механизм mmap.
Кроме того, была исследована зависимость времени, затрачиваемого на обмены данными в SMP-узловых кластерах в алгоритмах пульсации (рис. III.18). Время обменов мало различается во всех стратегиях, поэтому приводится только один график. Характерными его особенностями являются ожидаемый скачок в точке p=4, который объясняется вводом в действие сети передачи данных для обмена между процессами номер 3 и 4, оказавшимися на разных хостах. Далее наблюдается менее очевидная, но также объяснимая ступенька в точке p=8, когда хост, несущий процессы 4÷7, начинает по той же сети обмениваться уже с двумя внешними соседями — третьим и восьмым. Затем количество внешних соседей расти перестаёт, и мы видим слабый плавный рост времени обменов на графике. Последнее связано с необходимостью организации обменов суммарным значением невязки, а затраты на эту процедуру пусть и слабо, но зависят от количества узлов
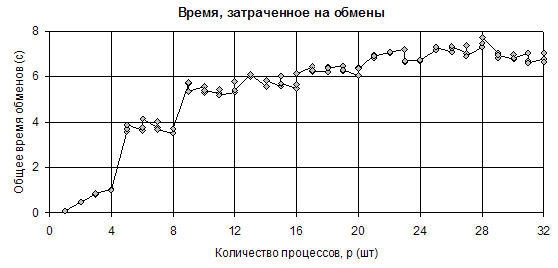
Рис. III.18. Зависимость времени, затраченного на обмены от количества процессов
Важнейшие публикации:
- Sadovskiy V. M.
On Mathematical Modeling of Granular Flow with Stagnant Zones // IV European Conf. on Computational Mechanics: Solids, Structures and Coupled Problems in Engineering (ECCM 2010). CD-ROM Proceedings. France, Paris: Springer. — 2010. — 2 p. - Дементьева Е. В., Карепова Е. Д.
Анализ параллельных реализаций МКЭ для моделей мелкой воды // V Сибирская конф. по параллельным и высокопроизводительным вычислениям. — Томск: Том. ун-т. — 2010. — С. 87-91. - Karepova E., Shaidurov V., Dementyeva E.
Parallel Implementation of Numerical Solution for Some Direct and Inverse Mathematical problems for Tidal Flows // 5th Int. Conf. «Inverse Problems: Modeling and Simulation» (IP:M&S). — Turkey, Izmir: Izmir University Publ. — 2010. — P. 78-79.
(Отделы Вычислительной математики, Вычислительной механики деформируемых сред, Служба средств телекоммуникаций и вычислительной техники)
| К началу | |