ИВМ СО РАН Поиск 
Отчеты ИВМ СО РАН

Отчет ИВМ СО РАН за 2010 год

Проекты СО РАН

Лаврентьевский грант молодым ученым СО РАН


Проект № 1. «Математическое моделирование движения людей»

Руководитель проекта: к.ф.-м.н. Е. С. Кирик

Проведены исследования динамических и стохастических свойств дискретной модели движения людей на характерных тестовых примерах.

На основе ранее полученных результатов разработана дискретно-непрерывная модель движения людей. Модель является непрерывной по пространству в выбранном направлении и дискретной с точки зрения количества возможных направлений перемещения человека. Предпосылкой к этому шагу стало следующее. Разработанная ранее модель движения людей была дискретной по времени и пространству. Но на практике порой в фокусе исследования оказывается изменение ширины проема, коридора в пределах 5-15 см. В силу размера ячейки (40 см на 40 см), дискретные модели являются «нечувствительными» к таким изменениям линейных размеров объекта, также затруднительным является задание людям разных размеров, скоростей, форм. Движение в непрерывном пространстве снимает эти ограничения, расширяет область применения модели, однако возрастает вычислительная сложность модели.

Каждый человек описывается диском определенного радиуса и присущей ему скоростью свободного движения. В каждый момент времени t положение каждого человека определяется по формуле


где →xi(t−Δt), [м] — координата в предыдущий момент времени; νi(t), [м/c] — скорость человека, определяемая по значению плотности и виду пути в направлении →ei(t); Δt, [c] — временной шаг.

Смещение в пространство, занятое недвижимым препятствием или другим человеком, невозможно. Направления →ei(t), i = 1,N и соответствующие величины сдвигов νi(t)Δt для всех людей определяются по определенному алгоритму с учетом других людей и препятствий (рис.V.14).

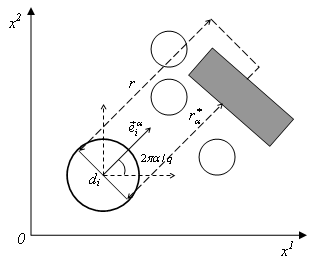
Рис. V.14
Рис. V.14. Схема построения области видимости в направлении

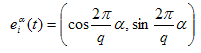
и взаимное расположение объектов

Численная реализация модели потребовала создания эффективных вычислительных алгоритмов расчета статического поля расстояний S до выходов, расчета локальной плотности, разрешения конфликтных ситуаций, движения по лестницам и др.

Результаты работы докладывались на конференциях:

  • Pedestrian and Evacuation Dynamics, США, Гайзерсбург, 7-11 марта 2010;
  • Cellular automata for research and industry, workshop «Crowds and cellular automata», Италия, Асколи-Пичено, 20-24 сентября 2010;
  • Моделирование неравновесных систем, Россия, г.Красноярск, 26-27 октября 2010.

Основные публикации:

  1. Kirik E., Yurgel'yan T., Krouglov D.
    On Influencing of a Space Geometry on Dynamics of Some CA Pedestrian Movement Model // Lecture Notes in Computer Science, Vol. 6350, Cellular Automata. — 2010. — P. 474–479.

  2. Кирик Е. С., Юргельян Т. Б., Круглов Д. В., Малышев А. В.
    О непрерывно-дискретной стохастической модели движения людей // Материалы XIII Всерос. сем. «Моделирование неравновесных систем». — Красноярск: ИВМ СО РАН. — 2010. — С. 81-85.

(Отдел моделирования неравновесных систем)

К началу

Webmaster