| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2012 год
Проекты СО РАН
- Программа сибирского отделения РАН «Телекоммуникационные и мультимедийные ресурсы СО РАН»
- Программа сибирского отделения РАН «Высокопроизводительные вычисления СО РАН»
- Междисциплинарные интеграционные проекты
- Проект № 21. «Исследование закономерностей и тенденций развития самоорганизующихся систем на примере веб-пространства и биологических сообществ»
- Проект № 44. «Геометрические и алгебраические методы нахождения точных решений уравнений математической физики и механики сплошных сред»
- Проект № 49. «Разработка и исследование методов компьютерного моделирования и обработки данных для информационно-управляющих систем поддержки принятия решений по повышению уровня пожарной безопасности зданий»
- Проект № 56. «Прогнозное моделирование и междисциплинарные комплексные исследования многолетней динамики состояния экосистем меромектических озер Сибири»
- Проект № 71. «Магнитные эффекты в биологически значимых системах»
- Проект № 116. «Микро- и наноразмерные многофазные неизотермические течения»
- Проект № 130. «Математические модели, численные методы и параллельные алгоритмы для решения больших задач СО РАН и их реализация на многопроцессоргых суперЭВМ»
- Проект № 131. «Математическое и геоинформационное моделирование в задачах мониторинга окружающей среды и поддержка принятия решений на основе данных стационарного, мобильного и дистанционного наблюдения»
- Проекты СО РАН, выполняемые совместно со сторонними научными организациями
- Экспедиционные проекты СО РАН
Междисциплинарные интеграционные проекты
Проект № 21. «Исследование закономерностей и тенденций развития самоорганизующихся систем на примере веб-пространства и биологических сообществ»
Руководитель проекта: член-корреспондент РАН А. М. Федотов
Ответственный исполнитель ИВМ СО РАН: д.т.н., профессор Л. Ф. Ноженкова
Исполнители: Е. В. Ковязина, Д. Д. Кононов, А. В. Коробко, Т. Г. Пенькова
Выполнено исследование применимости веб-метрик для оценки качества и востребованности информационных ресурсов Интернетf. В качестве экспериментальной базы использовались электронные каталоги и базы данных сети библиотек Красноярского научного центра СО РАН. Для большинства традиционных веб-метрик отсутствует их точное определение, а некоторые показатели, такие как посещение и обращение (хит), зависят от выбранных начальных параметров — времени и исключаемых типов файлов. Таким образом, количественные исследования информационных ресурсов и их сравнительный анализ требуют уточнения определений и однозначно заданных параметров для каждого конкретного исследования. Для исследования степени открытости ресурсов проведен анализ влияния на обращение к ресурсам ограничений на индексацию ресурсов роботами поисковых систем Интернет.
С целью выявления аналитических зависимостей в веб-пространстве научно-образовательного сообщества предложен подход к моделированию предметной области на основе технологии оперативной аналитической обработки данных (On-line Analytical Processing — OLAP) и метода анализа формальных понятий (Formal Concept Analysis — FCA). Интеграция технологий позволяет построить концептуальную OLAP-модель веб-пространства научно-образовательного сообщества, обеспечивающую возможность манипулировать объектами анализа и строить произвольные аналитические запросы.
Спроектирована концептуальная модель данных для хранения информации о сайтах, как элементах веб-пространства научного сообщества, которая позволяет сохранять полную информацию о сайтах, страницах и связях между ними. Кроме того, модель позволяет отслеживать динамику изменения элементов модели во времени с сохранением истории изменения. На основе концептуальной модели создана реляционная модель данных мониторинга контента. Разработаны параллельные алгоритмы обхода сайтов. Установлен сервер базы данных. Разработана мандатная ролевая модель безопасности, учитывающая специфику функционирования веб-приложений. Сформулировано утверждение о безопасности информационных потоков в системах, построенных на базе данной модели с учетом требований либерального мандатного управления доступом.
Выполнены работы по проектированию системы сбора информации о топологии и содержательных характеристиках веб-пространства. Выделены основные структурные единицы, их характеристики и возможные типы связей. Создана структура хранилища данных для анализа веб-пространства и алгоритмы работы системы сбора информации. Начаты работы по реализации программных средств. Составлен список научно-образовательных ресурсов Красноярского края для тестирования создаваемой системы.
Основные публикации:
- Korobko A. V., Penkova T. G.
Method of constructing the integral OLAP-model based on formal concept analysis // FFrontiers in Artifical Intelligence dence and Applications, 2012. — Is. 243. — P. 219–227 . - Кононов Д. Д.
Модель безопасности веб-приложений на основе мандатного ролевого разграничения доступа // Вестник Бурятского гос. ун.-та, 2012. — Вып. 9. — С. 29-33. - Ковязина Е. В.
Оценка работы библиотеки с помощью web-метрик // Материалы XII Междунар. конф. «Крым-2012», «Библиотеки и информационные ресурсы в современном мире науки, культуры, образования и бизнеса», 2012.
(Отделы прикладной информатики)
| К началу | |
Проект № 44. «Геометрические и алгебраические методы нахождения точных решений уравнений математической физики и механики сплошных сред»
№ гос. регистрации 01201255325
Руководитель проекта: академик РАН И. А. Тайманов, член-корреспондент РАН А. П. Чупахин, д.ф.-м.н. В. К. Андреев
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., профессор В. К. Андреев
Исполнители: В. Б. Бекежанова, И. В. Степанова
В отчетный период продолжены исследования, связанные с моделированием поверхностных волн в больших акваториях.
Блок: Структуры решений уравнений некоторых моделей гидродинамики.
1. Рассматривается двумерная модель термодиффузии
\[\rho _{0} \frac{du}{dt} ={\rm div}\prod {\rm +}\rho _{0} Fg,{\rm \; \; \; div\; }u=0,{\rm \; \; \; }\frac{dT}{dt} ={\rm div}(\chi \nabla T),{\rm \; \; \; }\, \] \[\frac{dC}{dt} ={\rm div(}D\nabla C+D^{T} \nabla T), \frac{dT}{dt} ={\rm div}(\chi \nabla T),\, \, \, \, \, \, \, \, \, \frac{dC}{dt} ={\rm div(}D\nabla C+D^{T} \nabla T),\]
где $\prod _{ij} =-p\delta _{ij} +2\rho _{0} \nu (\partial u_{i} /\partial x_{j} +\partial u_{j} /\partial x_{i} )\, $, $i,\, \, j=1,2$, $x=(x_{1}, \, \, x_{2} )$ — вектор координат, $u=(u_{1}, \, \, u_{2} )$ — вектор скорости жидкости, $p$ — давление, $g=(0,g)$ — вектор ускорения внешних сил, $\rho _{0} $ — плотность жидкости при средних значениях температуры и концентрации, $\textit{T}$ и $\textit{C}$ — отклонение температуры и концентрации от средних постоянных значений. Для неё решена задача групповой классификации относительно коэффициентов вязкости $\nu (T,C),\, \, $ температуропроводности$\chi (T,C)$, диффузии $D(T,C)$, термодиффузии$D^{T} (T,C)$ и функции $F(T,C)$, определяющей силу плавучести.
В предположении, что коэффициенты диффузии и температуропроводности не совпадают, подробно исследованы случаи, когда движение происходит под действием силы плавучести, а также в невесомости.
При решении задачи групповой классификации получены 6 классифицирующих уравнений, два из которых используются для определения функции, характеризующей силу плавучести; три, имеющих одинаковую дифференциальную структуру, — для вычисления коэффициентов вязкости, температуропроводности и диффузии; и одно, которое связано с последними двумя, — для нахождения коэффициента термодиффузии.
Основная группа преобразований наследуется из группы, допускаемой системой Навье-Стокса, за исключением преобразований поворота и растяжения.
Для упрощения зависимостей классифицируемых функций были вычислены преобразования эквивалентности, из которых следует, что коэффициенты переноса и сила плавучести определены с точностью до умножения на произвольную ненулевую постоянную. Для силы плавучести также справедливо преобразование эквивалентности сдвига на постоянную величину.
Анализ классифицирующих уравнений показал наличие 14 представлений для каждого из коэффициентов переноса от температуры и концентрации. В каждом из случаев допускаемая группа зависит от того, обращается сила плавучести в ноль или нет. Так, например, рассмотрим следующие зависимости коэффициентов переноса: $\nu =T^{m+n} f_{2} (w)$, $\chi =T^{m+n} f_{3} (w)$, $D=T^{m+n} f_{4} (w)$ и $D^{T} =T^{m+n-1} (k(f_{3} (w)-f_{4} (w))+f{}_{5} (w)).$ Здесь $f_{i} =f_{i} (w)$, $i=2,...,\, \, 5$, — произвольные гладкие функции аргумента $w=C-kT-q\ln T$, $m,\, \, n,\, \, k,\, \, q$ — произвольные постоянные. При такой зависимости коэффициентов сила плавучести может быть представлена формулой $F=T^{2m-n} f_{1} (w)$. Тогда уравнения помимо основной алгебры допускают оператор
\[(m-n)t\partial _{t} +nx_{1} \partial _{x_{1} } +nx_{2} \partial _{x_{2} } +mu_{1} \partial _{u_{1} } +mu_{2} \partial _{u_{2} } +2mp\partial _{p} +T\partial _{T} +kT\partial _{C} +q\partial _{C} .\]
В условиях невесомости ($F=0$) основную группу расширяют операторы
\[2t\partial _{t} +x_{1} \partial _{x_{1} } +x_{2} \partial _{x_{2} } -u_{1} \partial _{u_{1} } -u_{2} \partial _{u_{2} } -2p\partial _{p} ,\, \, \, x_{2} \partial _{x_{1} } -x_{1} \partial _{x_{2} } +u_{2} \partial _{u_{1} } -u_{1} \partial _{u_{2} } ,\] \[(m-n)t\partial _{t} +(m-n)x_{1} \partial _{x_{1} } +(m-n)x_{2} \partial _{x_{2} } +T\partial _{T} +kT\partial _{C} +q\partial _{C} .\]
При силе плавучести $F=-(s/g)\ln T+f_{1} (w)$, $s\ne 0$, коэффициенты переноса будут иметь следующий вид:
\[\nu =T^{3m} f_{2} (w), \chi =T^{3m} f_{3} (w), D=T^{3m} f_{4} (w), D^{T} =T^{3m-1} (k(f_{3} (w)-f_{4} (w))+f{}_{5} (w))\]
с тем же аргументом $w,$ что и в предыдущих формулах. Уравнения термодиффузии кроме основной алгебры допускают оператор
\[mt\partial _{t} +2mx_{1} \partial _{x_{1} } +2mx_{2} \partial _{x_{2} } +mu_{1} \partial _{u_{1} } +mu_{2} \partial _{u_{2} } +2mp\partial _{p} +s\rho _{0} x_{2} \partial _{p} +T\partial _{T} +kT\partial _{C} +q\partial _{C} .\]
Следует заметить, что получившиеся зависимости для искомых коэффициентов определены с точностью до произвольных функций. Тем самым, проведен первый этап группового анализа исходных уравнений термодиффузии.
2. Получены априорные оценки сопряжённой тепловой задачи
\[u_{1t} =\chi _{1} \left(u_{1rr} +\frac{2}{r} u_{1r} \right)+f_{1} (r,t),\, \, \, \, \, \, t \gt 0,\, \, \, \, \, \, r\in \Omega _{1},\] \[u_{2t} =\chi _{2} \left(u_{2rr} +\frac{2}{r} u_{2r} \right)+f_{2} (r,t),\, \, \, \, \, \, t \gt 0,\, \, \, \, \, \, r\in \Omega _{2},\] \[\left. u_{1} \right|_{t=0} =\left. u_{2} \right|_{t=0} =0, \left. u_{1} \right|_{r=R_{1} } =\left. u_{2} \right|_{r=R_{1} } =0,\] \[\left. k_{1} \frac{\partial u_{1} }{\partial r} \right|_{r=R_{1} } =\left. k_{2} \frac{\partial u_{2} }{\partial r} \right|_{r=R_{1} } ,\] \[\left. u_{2} \right|_{r=R_{2} } =0\]
в шаровых областях $\Omega _{1} =\left\{\left. r\right|0\le r \lt R_{1} \right\},$ $\Omega _{2} =\left\{\left. r\right|R_{1} \lt r \lt R_{2} \right\}.$ При этом существенно использовано неравенство
\[\int _{0}^{R_{1} }r^{2} w_{1}^{2} (r,t)dr+\int _{R_{1} }^{R_{2} }r^{2} w_{2}^{2} (r,t)dr\le \, M_{0} \left(k_{1} \int _{0}^{R_{1} }r^{2} \omega _{1r}^{2} (r,t)dr+k_{2} \int _{R_{1} }^{R_{2} }r^{2} w_{2r}^{2} (r,t)dr \right) .\]
Оно доказывается вариационным методом, причём постоянная $M_{0} $ не может быть уменьшена. Она удовлетворяет уравнению
\[F=\left(\frac{1-k}{\omega \sqrt{k} } -{\rm ctg}\left(\frac{R-1}{R} \omega \sqrt{k} \right)\right)\sin \omega +\sqrt{k} \cos \omega =0,\]
где $\omega =R_{1} (M_{0} {k_{1} \mathord{\left/ {\vphantom {k_{1} k_{2} }} \right.} k_{2} } )^{-{1\mathord{\left/ {\vphantom {1 2}} \right. } 2} }.$ Используя это неравенство, удаётся доказать ограниченность $\left|u_{j} \right|$ на своих областях определения на любом конечном промежутке времени $[0,T]$, если интегралы
\[\int _{0}^{T}\, \left(\int _{\Omega _{j} }^{}f_{j}^{2} (\xi ,\tau )d\xi \right) ^{{1\mathord{\left/ {\vphantom {1 2}} \right.} 2} } e^{\delta \tau } d\tau ={\rm const}\, {\rm \lt }\, \infty ,\, \, \, \, \, \, j=1,2,\]
сходятся с постоянной $\delta =M_{0}^{-1} \min ({\chi _{1} \mathord{\left/ {\vphantom {\chi _{1} k_{1} }} \right.} k_{1} }, {\chi _{2} \mathord{\left/ {\vphantom {\chi _{2} k_{2} }} \right.} k_{2} } ).$ При $T\to \infty \, \, $ $\left|u_{j} \right|\to 0$ и температуры стремятся к нулю.
Дано решение этой же задачи методом преобразования Лапласа. В образах по Лапласу решение находится в виде квадратур. Доказано, что если источники тепла имеют предел при $t\to \infty $, то и решение выходит на стационарный режим. Здесь же решена обратная задача по восстановлению источника тепла в ядре шара, если дополнительно на внешней поверхности шарового слоя задан поток тепла. При выводе априорных оценок основная трудность была в получении оценок поля температур в шаре. Принцип максимума здесь применять нельзя, так как коэффициенты имеют особенность в начале координат.
3. Известно (Г. Вебер, 1868), что уравнения движения идеальной несжимаемой жидкости, происходящего в потенциальном поле массовых сил, имеют общий интеграл в координатах Лагранжа. При этом начальное поле скоростей непосредственно входит в новую систему уравнений. В качестве искомых функций в этой системе выступают траектории и потенциал Вебера. Для плоских волн упомянутая выше система имеет вид
\[x_{t} =y_{\eta } \left(\varphi _{\xi } +u(\xi ,\eta )\right)-y_{\xi } \left(\varphi _{\eta } +v(\xi ,\eta )\right);~~~~~(V.1)\] \[y_{t} =-x_{\eta } \left(\varphi _{\xi } +u(\xi ,\eta )\right)+x_{\xi } \left(\varphi _{\eta } +v(\xi ,\eta )\right);~~~~~(V.2)\] \[x_{\xi } y_{\eta } -x_{\eta } y_{\xi } =1;~~~~~(V.3)\] \[u_{\xi } +v_{\eta } =0,\, \, \, \, \, \, v_{\xi } -u_{\eta } =\omega (\xi ,\eta )\ne 0;~~~~~(V.4)\]
где $x(\xi, \eta, t),\, \, y(\xi, \eta, t)$ — траектории, а $\varphi (\xi, \eta, t)$ — потенциал Вебера. По известным $x,\, y,\, \varphi $ давление восстанавливается по формуле
\[p(\xi ,\eta ,t)=\frac{1}{2} (x_{t}^{2} +y_{t}^{2} )-\varphi _{t} +h(\xi ,\eta ,t).\]
Для системы (V.1) — (V.3) решена задача групповой классификации по отношению к функциям $u(\xi, \eta ),$ $v(\xi, \eta ),$ связанным соотношениями (V.4). Преобразования эквивалентности — это группа преобразований, сохраняющих площадь.
Для координат оператора системы (V.1) — (V.3) находим
\[\xi ^{1} =\xi ^{1} (t),\quad \xi ^{2} =\xi ^{2} (\xi ,\eta ),\quad \xi ^{3} =\xi ^{3} (\xi ,\eta ),\] \[\eta ^{1} =C_{1} x+C_{2} y+n(t),\quad \eta ^{2} =C_{1} y-C_{2} x+m(t),\] \[\eta ^{3} =(2C_{1} -\xi _{t}^{1} )\varphi +n_{t} x+m_{t} y+h(\xi ,\eta )+d(t),\] \[\xi _{\xi }^{2} +\xi _{\eta }^{3} =2C_{1} ,\quad u(\xi _{\eta }^{3} -\xi _{t}^{1} )-\xi ^{2} u_{\xi } -\xi ^{3} u_{\eta } -\xi _{\xi }^{3} v-h_{\xi } =0,\] \[v(\xi _{\xi }^{2} -\xi _{t}^{1} )-\xi ^{2} v_{\xi } -\xi ^{3} v_{\eta } -\xi _{\eta }^{2} u-h_{\eta } =0.\]
Из двух последних получаем классифицирующее уравнение на начальный вихрь:
\[\xi ^{2} \omega _{\xi } +\xi ^{3} \omega _{\eta } +C_{3} \omega =0.\]
Базис основной алгебры Ли $L_{0} $ образован операторами
\[L_{0} \, :Y_{1} =\partial _{t} ,\quad Y_{2} =y\partial _{x} -x\partial _{y} ,\quad Y_{n} =n(t)\partial _{x} +n_{t} (t)x\partial _{\varphi } ,\] \[Y_{m} =m(t)\partial _{y} +m_{t} (t)y\partial _{\varphi } ,\quad Y_{d} =d(t)\partial _{\varphi } .\]
При $\omega ={\rm const}$ к $L_{0} $ добавляются операторы
\[Y_{\psi } =\psi _{\eta } \partial _{\xi } -\psi _{\xi } \partial _{\eta } +h\partial _{\varphi } ,\quad Y_{3} =\xi \partial _{\xi } +\eta \partial _{\eta } +x\partial _{x} +y\partial _{y} +(2\varphi +h)\partial _{\varphi } ,\]
а при $\omega \ne {\rm const}$ —
\[Y_{F} =\frac{\partial F(\omega )}{\partial \eta } \, \partial _{\xi } -\frac{\partial F(\omega )}{\partial \xi } \, \partial _{\eta } , Y_{4} =\delta t\partial _{t} +\xi \partial _{\xi } +\eta \partial _{\eta } +x\partial _{x} +y\partial _{y} +(2-\delta )\varphi \partial _{\varphi } .\]
Начальная завихренность равна $\omega (\xi, \eta )=\eta ^{-\delta } f(\xi /\eta ).$
Требование инвариантности начальных условий $x=\xi, y=\eta, t=0$ приводит к более детальной классификации — специализации завихренности $\omega$. Всего выделено 16 таких функций и найдены допускаемые операторы.
Основные публикации:
- Краснова Д. А.
Групповые свойства уравнений движения плоского слоя идеальной жидкости // Материалы науч. конф. «Герценовские чтения — 2012». — СПб, 2012. — С. 78-82. - Андреев В. К., Резникова И. А.
Оценки решений сопряжённой тепловой задачи в шаровой области // J. of Siberian Federal University. Mathematics and Physics, 2012 (в печати). - Stepanova I. V.
Group classification for equations of thermodiffusion in binary mixture // Communication in Nonlinear Science and Numerical, 2012 (в печати).
(Отдел дифференциальных уравнений механики)
| К началу | |
Проект № 49. «Разработка и исследование методов компьютерного моделирования и обработки данных для информационно-управляющих систем поддержки принятия решений по повышению уровня пожарной безопасности зданий»
№ гос. регистрации 01201268795
Руководитель проекта: член-корреспондент РАН В. В. Шайдуров
Ответственный исполнитель ИВМ СО РАН: д.т.н., проф. Л. Ф. Ноженкова
Исполнители: А. А. Евсюков, Е. С. Кирик, Р. В. Морозов
Разработана объектно-ориентированная модель представления знаний для поддержки превентивных мероприятий по снижению уровня пожароопасности зданий. Информация в базе знаний описывает условия возможных сценариев пожара и соответствующие им способы формирования решений. Реализован подход к поддержке принятия решений, включающий в себя анализ состояния объекта на основе моделирования развития пожара и эвакуации, расчета риска в условиях текущей эксплуатации объекта; формирование рекомендаций для поддержки принятия решений по снижению влияния рискообразующих факторов; моделирование различных сценариев развития пожара и эвакуации с применением наглядной 3D-визуализации — трехмерного поэтажного изображения объекта.
Выполнена пространственно-временная адаптация параметров полевой модели движения людей. Одним из ключевых параметров, отвечающих за скорость человека, двигающегося в потоке людей, является плотность потока. В разрабатываемой полевой стохастической модели движения людей индивидуально-поточного типа скорость человека определяется через такую явную связь. Локальная плотность потока является ключевым параметром при определении скорости человека на каждом расчетном шаге. В рамках проекта проведена работа по исследованию нескольких численных алгоритмов оценивания локальной плотности потока с учетом специфики задачи. Спецификой задачи в данном случае являются: определение области локализации (которая зависит в общем случае от текущей ситуации), минимизация количества вычислительных операций, универсальность метода при поддержании приемлемой точности оценки плотности, работа с «удобными» единицами измерения плотности. В результате проведенных исследований был скорректирован используемый расчетный алгоритм оценивания плотности.
Разработаны алгоритмы распараллеливания вычислений либо для одного многопроцессорного узла, либо для MPI-кластера путем разнесения поэтажных расчетов по отдельным процессам и организации обмена между процессами согласно стандарту MPI (Message Passing Interface).
Основные публикации:
- Kirik Е., Vitova T.
On validation of the SIgMA.CA pedestrian dynamics model with bottleneck flow // Lecture Notes in Computer Science, 2012. — V. 7495, ACRI Proceedings. — P. 719–727 . - Евсюков А. А.
Трехмерная визуализация процессов распространения дыма и эвакуации людей // Материалы Х Всерос. заоч. конф. по теоретическим основам проектирования и разработки распределенных информационных систем «ПРИС-2012». — Красноярск, 2012. — С.99–104 . - Морозов Р. В.
Использование современных информационных технологий для построения управляющей системы «ПБ ЭКСПЕРТ» // Материалы Х Всерос. заоч. конф. по теоретическим основам проектирования и разработки распределенных информационных систем «ПРИС-2012». — Красноярск, 2012. — С. 104–108 .
(Отделы Вычислительной математики, Прикладной информатики)
| К началу | |
Проект № 56. «Прогнозное моделирование и междисциплинарные комплексные исследования многолетней динамики состояния экосистем меромектических озер Сибири»
Руководитель проекта: академик РАН А. Г. Дегерменджи
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. В. М. Белолипецкий
Исполнители: В. М. Белолипецкий, Л. А. Компаниец, С. Н. Генова, Т. В. Якубайлик, П. В. Белолипецкий
Разработана компьютерная модель, основанная на одномерном приближении, для расчетов сезонных изменений вертикальных распределений температуры и солености воды в стратифицированном озере с учетом образования и таяния льда. Выполнено интегрирование компьютерной программы, реализующей одномерную вертикальную математическую модель для определения температурного и солевого режимов озера в приложение Excel. Проведена автоматизация работы средствами VBA для удобного исследования различных сценариев поведения объекта в зависимости от метеоданных и других параметров, а также для сохранения полученных результатов в виде таблиц и графиков для анализа результатов. Выполнены качественные оценки влияния внутренних волн на колебания температуры воды в металимнионе.
Проведены натурные измерения скоростей течений в озере Шира в летний период. В результате анализа проведенных натурных измерений скоростей течений в озере Шира были обнаружены колебания вертикальной компоненты скорости течения, что характерно для внутренних волн в стратифицированном водоеме.
В рамках соглашения о двустороннем сотрудничестве с Атлантическим отделением Института океанологии им. П. П. Ширшова РАН на 9 разрезах оз. Шира проведены непрерывные измерения вектора скорости по всей глубине, позволяющие определить картину трехмерного течения в целом. Наличие внутренних волн различных масштабов в озере Шира в летний период подтверждается также анализом данных температуры и давления, полученных с использованием распределенных датчиков температуры. Выполнены измерения уровня воды в озере Шира (рис. V.4).
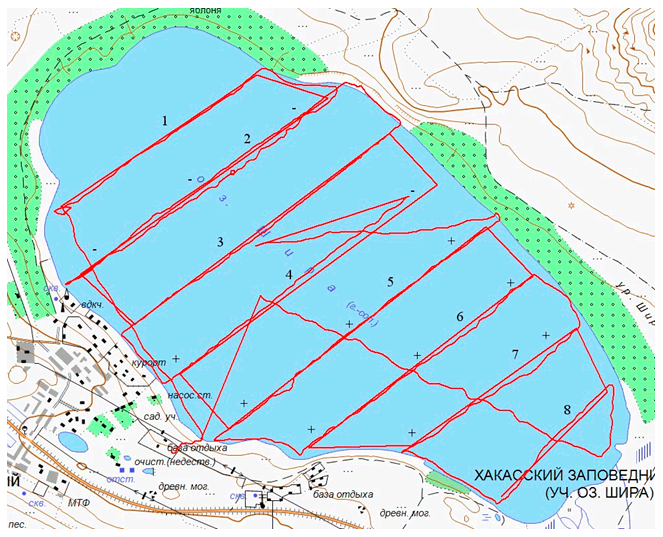
Рис. V.4. Направления галсов, по которым проводились измерения, и картина подъема и опускания внутренних вод (знак "+" соответствует положительной вертикальной скорости, знак «-» — отрицательной) по состоянию на 4 августа 2012 г.
Основные публикации:
- Компаниец Л. А., Якубайлик Т. В., Володько О. С.
Анализ характеристик озера Шира на основе натурных данных // Вестник Бурятского гос. ун-та. Математика. Информатика, 2012. — Вып. 9. — С. 167–176 . - Yakubaylik T. V., Guldenbalk Yu. B., Kompanieets L. A.
Theoretical justification of the possible internal waves in the Lake Shira // Selected and Reviewed Papers Int. Conf. on environmental observations, modeling and information systems. — Irkutsk, 2012. — P. 105–107 .
(Отделы Вычислительных моделей в гидрофизике)
| К началу | |
Проект № 71. «Магнитные эффекты в биологически значимых системах»
№ гос. регистрации 01201259038
Руководители проекта: академик РАН Ю. Н. Молин
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., профессор В. М. Садовский
Этап 2012 г. Создание параллельных методов расчета спиновой динамики в полуклассическом приближении по сверхтонкому взаимодействию радикалов с магнитными ядрами.
Для численного исследования задач спиновой химии предложен и программно реализован специальный алгоритм обращения преобразования Лапласа, основанный на многократном применении быстрого преобразования Фурье. В этом алгоритме при вычислении интеграла Меллина используются алгебраически точные квадратурные формулы Гаусса высокого порядка. С помощью разработанного алгоритма выполнены расчеты объемной рекомбинации радикалов на двумерной плоскости.
Совместно с МТЦ СО РАН разработаны пробные версии параллельных вычислительных алгоритмов и программ для систем с графическими ускорителями, реализующие принципиально новый способ обработки эхо-сигналов в магнитно-резонансном томографе, основанный на использовании производящих функций. В однопроцессорном варианте завершен алгоритм, в котором разложение производящей функции в степенной ряд осуществляется с помощью быстрого преобразования Фурье, а минимизация целевой функции производится симплекс-методом Нелдера-Мида. С целью верификации программ проведено сравнение результатов расчетов с экспериментальными измерениями. Выявлены недостатки алгоритма, требующие его существенной доработки. Рассмотрены два варианта задания целевой функции при реализации алгоритма обработки эхо-сигналов в магнитно-резонансном томографе. Первый вариант основан на методе наименьших квадратов по взвешенной норме, во втором минимизируется корреляция векторов расчетного и полученного в измерениях эхо-сигналов. Разработаны компьютерные программы минимизации целевых функций на основе метода градиентов с проекцией и метода Левенберга-Марквардта, проведены сравнительные расчеты.
Для описания процесса спин-селективной рекомбинации радикалов на сферической поверхности мицеллы разработан алгоритм и компьютерная программа для численного решения вырождающегося обыкновенного дифференциального уравнения Лежандра с граничным условием второго рода. Показано, что используемая разностная схема безусловно устойчива и имеет второй порядок точности. Проведена верификация программы на тестах — точных решениях задачи со специальным выбором коэффициентов уравнения.
Основные публикации:
- Лукзен Н. Н., Иванов К. Л., Садовский В. М., Каптейн Р., Сагдеев Р. З.
Магнитные и спиновые эффекты в объемной рекомбинации радикалов на двумерной плоскости // Докл. академии наук (в печати). - Lukzen N. N., Ivanov K. L., Sadovsky V. M., Kaptein R., Sagdeev R. Z.
Magnetic and Spin Effects on the Recombination of Radicals on Two-Dimensional Surfaces // Doklady Physical Chemistry (в печати).
(Отдел вычислительной механики деформируемых сред)
| К началу | |
Проект № 116. «Микро- и наноразмерные многофазные неизотермические течения»
Руководитель проекта: член-корреспондент РАН С. В. Алексеенко
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. В. К. Андреев
Исполнители: В. Б. Бекежанова, М. В. Ефимова
Блок: Пленочные течения при спутном потоке газа и их устойчивость.1. Изучена задача о совместном течении жидкой плёнки и спутного потока газа. На поверхности раздела в качестве энергетического условия принимается полное условие, учитывающее энергию, затрачиваемую термокапиллярными силами на деформацию поверхности. Исследуется устойчивость течения плёнки относительно плоских и пространственных возмущений. Выделены наиболее опасные моды и построена карта режимов течения. Проведено сравнение полученных результатов с решением аналогичной задачи в классической постановке, когда на поверхности раздела задаётся равенство потоков тепла без учёта дополнительного слагаемого. Имеет место смена механизмов неустойчивости и наиболее опасных мод: с монотонной (в классической задаче) на колебательную (в задаче с полным энергетическим условием). В последнем случае неустойчивость течения плёнки связана с развитием бегущих тепловых волн.
В качестве энергетического условия на поверхности раздела жидкость-газ используется полное условие
\[k_{g} \frac{\partial T_{g} }{\partial n} (x,h(x))-k_{l} \frac{\partial T_{l} }{\partial n} (x,h(x))=\kappa T\nabla _{11} \cdot v,\]
где выражение в правой части описывает энергию, затраченную на деформацию поверхности раздела термокапиллярными силами.
Учёт дополнительного слагаемого позволил получить результат, качественно соответствующий экспериментальным данным для системы FC-72 (жидкость) и азота (газ). При нормальной гравитации кризис течения вызван тепловой колебательной модой и сопровождается формированием поперечных бегущих гидротепловых волн (рис. V.5а), которые распространяются в противоположном основному течению направлении (рис. V.6а).
Проведено сравнение со случаем, когда в качестве энергетического условия принимается равенство потоков тепла. В отсутствие дополнительного слагаемого наиболее опасной является монотонная тепловая мода и неустойчивость проявляется в виде стоячих тепловых волн (рис. V.5б, V.6б).
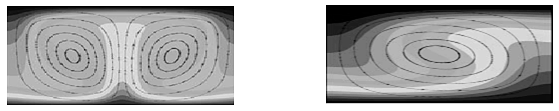
Рис. V.5 а, б
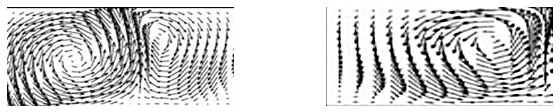
Рис. V.6 а, б. Картина течения в области формирования вихрей
В условиях пониженной гравитации также наблюдается формирование поперечных волн (рис. V.7а,б). Однако в случае использования полного граничного условия амплитуды и длины этих волн существенно выше (рис. V.8а), чем во второй задаче (рис. V.8б).

Рис. V.7 а, б

Рис. V.8 а, б
Исследовано влияние сил Марангони на характер возникающих неустойчивостей, которые могут приводить к различным формам течения. Карта режимов течений в условиях нормальной гравитации представлена на рис. V.9а, V.9б.
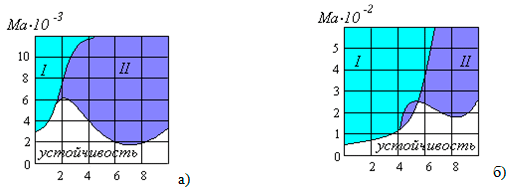
Рис. V.9. Нейтральные кривые а) с учётом энергии, затраченной на деформацию поверхности раздела; б) при условии равенства потоков тепла на поверхности раздела
Рост волнового числа приводит к расщеплению монотонной нейтральной кривой на две: монотонную и колебательную. В зоне I имеет место термокапиллярная неустойчивость, которая проявляется в форме продольных валов, оси которых параллельны направлению основного течения. При этом наиболее опасной является монотонная мода. В области II кризис течения индуцируется бегущими тепловыми волнами, которые распространяются в противоположном основному течению направлении и соответствуют колебательному режиму неустойчивости. При этом нейтральные кривые имеют два минимума: в длинноволновой и коротковолновой области.
2. Исследовано совместное однонаправленное движение вязкой теплопроводной жидкости и бинарной смеси в цилиндрической трубке. Жидкость образует слой на твёрдой стенке трубки и контактирует со смесью через поверхность раздела. Движение этих сред вызывается заданным постоянным градиентом температуры вдоль твёрдой поверхности и, вообще говоря, нестационарным градиентом давления. Осевые скорости, возмущения температур и концентрации являются решением линейной сопряжённой задачи со сложными условиями на поверхности раздела где — радиус стенки цилиндра. На границе раздела поверхностное натяжение линейно зависит от температуры и концентрации. Найдено стационарное течение и показано, что даже если оно формируется только под действием термокапиллярных сил, то в нём могут возникать зоны возвратного течения. Этот эффект связан с ненулевой кривизной поверхности раздела. Нестационарное решение определяется методом преобразования Лапласа. Доказано, что если градиент давления в смеси при стремится к постоянному, то и движение выходит на стационарный режим.
3. Изучена задача о совместном движении вязкой жидкости и плёнки бинарной смеси, находящейся на твёрдой подложке. Найдено специальное решение сопряжённой задачи уравнений вязкой теплопроводной жидкости и уравнений термодиффузии, при котором поверхность раздела всегда остаётся плоской и неподвижной. Оно описывает совместное однонаправленное движение в слое с твёрдыми стенками, причём на последних задан постоянный градиент температуры, который и вызывает это движение. Показано, что с ростом времени решение по экспоненциальному закону выходит на стационарный режим. На основе численного анализа обнаружено, что с ростом времени функции скорости и температуры выходят на стационарный режим. Для распределения концентрации это справедливо лишь когда ее продольный градиент равен нулю.
Основные публикации:
- Бекежанова В. Б., Кабов О. А.
Влияние термокапиллярного эффекта на формирование вторичных режимов плёночного течения // ЖЭТФ, 2012 (в печати). - Ефимова М. В.
Совместное движение бинарной смеси и вязкой жидкости под действием термоконцентрационных сил // J. of Siberian Federal University. Mathematics and Physics, 2012 (в печати). - Andreev V. K.
The motion of a binary mixture and viscous liquid in a circular pipe // Abstracts of the 2nd Int. Conf. on Scientific Computing in Aerodynamics. Beihang University, Beijing, China, 2012. — P. 29.
(Отдел дифференциальных уравнений механики)
| К началу | |
Проект № 130. «Математические модели, численные методы и параллельные алгоритмы для решения больших задач СО РАН и их реализация на многопроцессоргых суперЭВМ»
Руководитель проекта: академик РАН Б. Г. Михайленко
Ответственный исполнитель от ИВМ СО РАН: к.ф.-м.н., доцент Е. Д. Карепова
Исполнители: В. В. Шайдуров, Е. В. Дементьева
Исследуются различные аспекты математического и численного моделирования приливных течений и поверхностных волн в больших открытых акваториях.
В рассмотренной модели для однозначного определения решения задачи необходимо наряду со скоростями и отметками уровня свободной поверхности $\xi $ определить влияние океана на открытую часть границы $\Gamma _{2} $ расчетной области, представленную в модели неизвестной функцией $\textit{d}$ в граничных условиях. Обратная задача ставится на каждом шаге по времени после дискретизации по времени начально-краевой задачи, моделирующей распространение поверхностных волн в больших акваториях с учетом сферичности Земли и ускорения Кориолиса на основе осредненных по вертикали уравнений движения и неразрывности.
Исследована разрешимость обратной задачи о граничной функции, использующей некоторую дополнительную информацию (данные наблюдений) о возвышении свободной поверхности $\xi _{obs} $ на части открытой границы. Поскольку получившаяся задача некорректна, то для ее решения с приемлемой точностью применены методы, разрабатываемые для некорректных обратных задач математической физики проф. В.И. Агошковым с использованием методов оптимального управления.
В работе на основе данных наблюдений определяется функционал качества, адекватно отвечающий рассматриваемой задаче, при этом исходная обратная задача сводится к задаче минимизации введенного функционала на каждом шаге по времени. Причем для регуляризации в функционал качества по методу А. Н. Тихонова вводится стабилизирующий член, зависящий от пространства, в котором ищется неизвестная граничная функция.
Предложен, исследован и реализован итерационный алгоритм восстановления по данным наблюдений неизвестной граничной функции $\textit{d}$, описывающей влияние океана через открытую границу $\Gamma _{2} $ расчетной области, состоящий из последовательного решения прямой и сопряженной задач, а также уравнения для уточнения граничной функции.
В численных экспериментах в качестве расчетной области $\Omega$ рассмотрена акватория Охотского моря и прилегающий к Курильским островам участок Тихого океана. Поскольку в общем случае для нестационарной задачи начальные данные неизвестны, а рассматриваемая процедура не предполагает их восстановления, то для определения начальных данных в $\Omega $ решалась задача на установление, решение которой и использовалось в качестве начальных данных. За наблюдаемые данные на границе $\Gamma _{0} $ принимались значения свободной поверхности $\xi $ из установившегося решения (иногда с наложенным белым шумом, иногда с пропусками), а значения граничной функции $d$ «забывались».
Рассмотрено восстановление граничной функции в пространствах $L_{2} (\Gamma _{2} )$, $W_{2}^{1} (\Gamma _{2} )$, $W_{2}^{1/2} (\Gamma _{2} )$. Показано, что в последних двух случаях для восстановления с приемлемой точностью можно использовать меньше данных наблюдений или зашумленные данные. Далее графики функций приведены вдоль восточной границы $\Omega $, соответствующей $\lambda =161,5^{\circ } $ в.д.
Зашумленные данные наблюдений. В экспериментах в качестве наблюдаемых данных рассматривалась функция $\xi _{obs} $ с наложенным «белым шумом». Полученная возмущенная функция и использовалась при восстановлении. Рис. V.10 демонстрирует процесс восстановления граничной функции $d$ и возвышения свободной поверхности $\xi $ на границе по Тихому океану области $\Omega $.
Если граничная функция $d$ восстанавливается в $L_{2} (\Gamma _{2})$ или пространстве следов $W_{2}^{1/2} (\Gamma _{2} )$, то $\xi $ на границе восстанавливается к зашумленным значениям, т.е. к заданным данным «наблюдений» (рис. V.10 b, f). Процесс восстановления является чувствительным к внесенным в данные наблюдений погрешностям. Например, отклонение $d$ от точного решения в экспериментах достигает 22% (рис. V.10 e). При восстановлении $d$ в пространстве $W_{2}^{1} $ функции $d$ и $\xi $ сохраняют свою гладкость и стремятся к точному решению (рис. V.10 c, d).
Данные наблюдений с пропусками. В численных экспериментах решалась задача на восстановление функции $d$ в случае, когда всюду на границе по Тихому океану были заданы гладкие данные наблюдений с одним пропуском на границе $\lambda =161,5^{\circ } $.
Результаты численного эксперимента представлены на рис. V.11. Из рис. V.11 a, b видно, что в $L_{2} (\Gamma _{2} )$ граничная функция $d$ и $\xi $ восстанавливаются только в точках, где наблюдения были заданы, в то время как при восстановлении $d\in W_{2}^{1} (\Gamma _{2} )$ функции $d$ и $\xi $ восстанавливаются во всех точках жидкой границы, включая не наблюдаемые (рис. V.11 c-d). Из рис. V.11 d видно, что рассмотренный в работе алгоритм в пространстве следа восстанавливает уровень свободной поверхности $\xi $ с небольшой погрешностью (около $3% $) в точке, в которой данные наблюдений не были заданы. Функция $d$ восстанавливается менее точно, отклонение от точного решения в эксперименте достигает $16% $ на месте пропуска (рис. V.11 f). Итерационный процесс сходится быстрее, чем при восстановлении в пространстве $W_{2}^{1} (\Gamma _{2} )$, в тестовых экспериментах за 13 итераций против 71.
Результаты экспериментов, приведенные на рис. V.10 — V.11 показывают, что на характер восстановленных значений $d$ и $\xi $ главным образом влияет выбор пространства поиска граничной функции $\textit{d}$. При восстановлении $d$ в пространстве следа $W_{2}^{1/2} $ восстановленная функция, с одной стороны, сохранила чувствительность к внесенным погрешностям, присущую восстановлению в $L_{2} (\Gamma _{2} )$, с другой стороны, способность восстанавливать пропуски, как в $W_{2}^{1} (\Gamma _{2} )$. Взаимное влияние и пересечение этих свойств хорошо иллюстрируется результатами эксперимента при восстановлении с пропусками, когда граничная функция пытается восстановиться до «полностью» гладкой, как в $W_{2}^{1} (\Gamma _{2} )$, но при этом учесть и отразить форму начальных данных, как в $L_{2} (\Gamma _{2} )$.
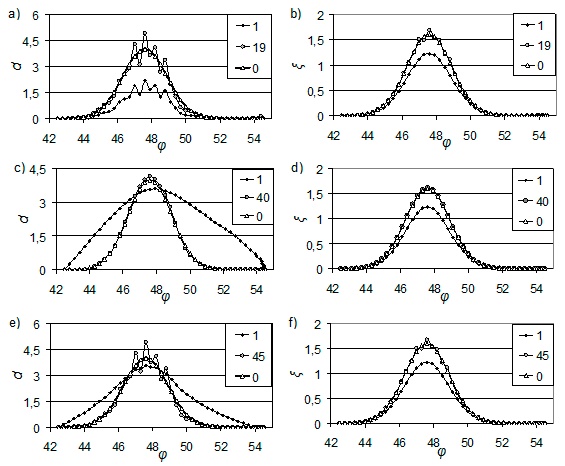
Рис V.10. Восстановление функций d (слева) и $\xi$ (справа) на одной из жидких границ $\Omega $ по зашумленным данным наблюдений. В пространстве $L_{2} (\Gamma _{2} )$ — a) и b); в пространстве $W_{2}^{1} (\Gamma _{2} )$ — c) и d); в пространстве $W_{2}^{1/2} (\Gamma _{2} )$ — e) и f). Приведены графики для первой и последней итераций, кривая, помеченная «0» соответствует точным значениям d и $\xi$
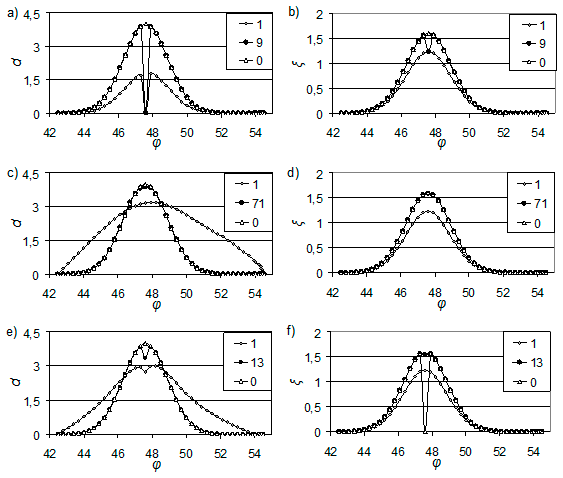
Рис. V.11. Восстановление функций d (слева) и $\xi$ (справа) на одной из жидких границ $\Omega $ по данным наблюдений, заданным с пропусками. В пространстве $L_{2} (\Gamma _{2} )$ — a) и b); в пространстве $W_{2}^{1} (\Gamma _{2} )$ — c) и d); в пространстве $W_{2}^{1/2} (\Gamma _{2} )$ — e) и f). Приведены графики для первой и последней итераций, кривая, помеченная «0» соответствует точным значениям d и $\xi$
Основные публикации:
- Karepova E., Dementyeva E.
The numerical solution of the inverse problem for shallow water models // Lecture Notes in Computer Science, 2012. (в печати). - Дементьева Е. В., Карепова Е. Д., Шайдуров В. В.
Восстановление граничной функции по данным наблюдений для задачи распространения поверхностных волн в акватории с открытой границей // СибЖИМ, 2013. (в печати). - Дементьева Е. В., Карепова Е. Д., Шайдуров В. В.
Ассимиляция наблюдаемых данных в задаче распространения поверхностных волн в акватории с открытой границей // Russian J. of Numer. Analysis and Mathem. Model., 2013. (в печати).
(Отдел вычислительной математики)
| К началу | |
Проект № 131. «Математическое и геоинформационное моделирование в задачах мониторинга окружающей среды и поддержка принятия решений на основе данных стационарного, мобильного и дистанционного наблюдения»
Руководитель проекта: академик РАН Ю. И. Шокин
Ответственный исполнитель от ИВМ СО РАН: к.ф.-м.н. О. Э. Якубайлик
Исполнители: А. А. Кадочников, А. Г. Матвеев, А. С. Пятаев
Исследования и результаты отчетного этапа связаны с анализом существующих систем экологического мониторинга, проблемами и особенностями реализации в них технологических цепочек для получения, передачи, хранения и использования данных. Рассматривались соответствующие информационные модели и структуры данных, формулировались критерии оценки их эффективности, требования к информационно-аналитическому обеспечению. Результатом выполнения работ стало формирование типовой подсистемы ГИС мониторинга — базы данных с результатами наблюдений за состоянием окружающей природной среды. Также проводились исследования, посвященные проектированию и разработке, модернизации программно-технологического обеспечения для построения прикладных геоинформационных веб-систем (геопорталов). Основное внимание уделялось развитию технологий для работы с пространственными метаданными. Создана система управления контентом интерактивного картографического веб-портала «Геофреймворк», которая предоставляет базовый набор средств для разработки геоинформационных веб-приложений, а также веб-приложение для визуализации каталога пространственных данных.
Разработка информационных и геоинформационных моделей для систем мониторинга с учетом анализа требований типовых моделей наблюдений и потоков данных. Разработка алгоритмов системного анализа применительно к задачам моделирования состояний геосистем, определение функциональных критериев оптимизации информационных потоков.
Для хранения результатов наблюдений на тестовых площадках разработана концептуальная модель базы данных. Наблюдения за состоянием окружающей среды разбиты на этапы мониторинга. Предполагается, что в ходе каждого этапа выполняется несколько экспедиций на различные площадки наблюдения (например, Ванкорское нефтегазовое месторождение, Юрубченское нефтегазовое месторождение и др.). На каждой площадке наблюдения размещены отдельные пункты наблюдения (В1, В2 и др.), на которых проводится отбор проб.
Все показатели мониторинга разбиты по тематическим разделам — качество атмосферного воздуха, качество поверхностных вод, качество почв, и др. У показателей заданы единицы измерения и предельно допустимая концентрация (ПДК). Результаты замеров собираются в многомерной таблице фактов (значение показателя). Измерениями таблицы являются экспедиция, пункт наблюдения, показатель. В мерах фиксируется значение показателя, погрешность измерения, комментарий, дата измерения, ссылка на прибор и метод измерения.
Программная реализация базы данных результатов наблюдений выполнена как составная часть (подсистема) общей ГИС-мониторинга состояния окружающей среды. Для нее предусмотрено два вида доступа — пользовательский и административный (рис. V.12). В настоящее время созданы прототипы веб-интерфейсов.
Административный веб-интерфейс доступен пользователям после предварительной авторизации. В нем реализованы функции управления структурой наблюдаемых объектов (площадки наблюдения, экспедиции, этапы наблюдения), системы показателей (разделы, показатели), добавление и редактирование результатов измерений. Поддерживается импорт и экспорт данных в формате CSV. При импорте данных выполняется автоматическое связывание со справочниками системы по кодам элементов.
Клиентский веб-интерфейс предоставляет средства для выборки и визуализации данных. На текущий момент реализовано два отчета — отчет по данным мониторинга и отчет по участкам измерения. Первый отчет предназначен для подготовки выборки сырых данных из многомерной таблицы фактов. С помощью фильтра возможно выбирать различные срезы данных. В возвращаемой таблице результатов выполняется тематическая раскраска отдельных значений в зависимости от превышения ПДК.
Отчет по участкам предназначен для анализа загрязнения окружающей среды между отдельными участками и в динамике по отдельному показателю. Результирующая выборка отображается в виде графика и таблицы.
В процессе выбора параметров фильтра выполняется динамическая подстройка других параметров в зависимости от наличия или отсутствия данных с такими характеристиками. Т.е. если пользователь задает этап мониторинга, например «1 этап 2012 года», то список доступных площадок и показателей будет автоматически скорректирован. В новых списках будут только те значения параметров, по которым есть данные. Рядом с элементами списков отображается количество доступных значений показателей, которые удовлетворяют условиям фильтрации. Далее, если пользователь выберет конкретную площадку, например «Ачинский НПЗ», то в списке показателей останутся только те показатели, по которым есть данные для «Ачинского НПЗ» в рамках «1 этапа 2012 года». Фильтрация списков выполняется асинхронно, без перезагрузки основной страницы, что удобно для пользователя.
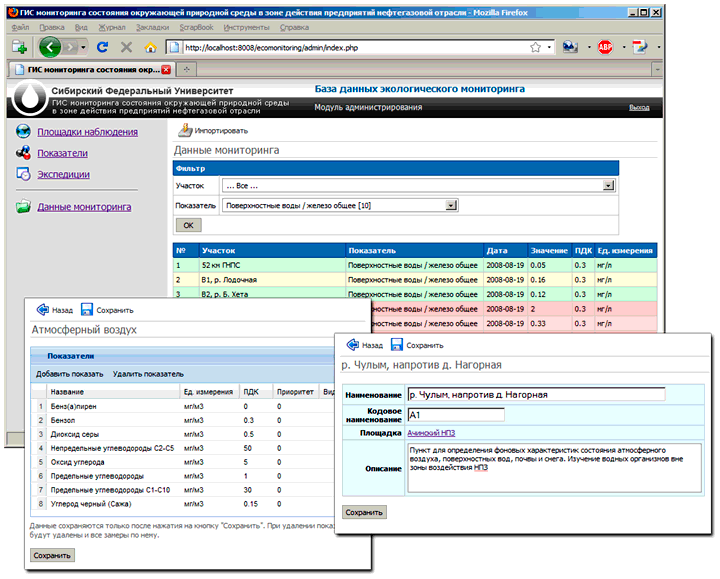
Рис. V.12. Прототип пользовательского интерфейса базы данных типовой подсистемы ГИС мониторинга
Реализация прототипа выполнена на основе СУБД PostgreSQL 8.x с модулем PostGIS, языка сценариев PHP 5.x, а также ряда свободно распространяемых программных библиотек и модулей — jQuery, Ext2js, HTML_MetaForm, TinyMCE, Smarty, PEAR, Zend Framework, и др.
Развиваемый подход основан на комплексе информационно-вычислительного обеспечения, который включает сервисы и средства хранения, обработки и анализа пространственных данных (в том числе — спутниковых изображений), библиотеки прикладных программных и пользовательских интерфейсов, средства авторизации доступа в составе геопортала и каталог пространственных метаданных, систему картографической веб-визуализации, служебных и прикладных веб-сервисов.
Создана система управления контентом интерактивного картографического веб-портала «Геофреймворк», которая предоставляет базовый набор средств для разработки геоинформационных веб-приложений. Основной упор при формировании данной системы был сделан на расширяемость функционала, гибкость в формировании пользовательских интерфейсов, поддержку современных веб-технологий, независимость от систем хранения данных. Для этого были использованы объектно-ориентированные технологии, шаблон проектирования MVC, и проч.
На основе системы «Геофреймворк» и оригинальной библиотеки интеграции веб-приложений с системой управления пространственными данными было создано веб-приложение для визуализации каталога пространственных данных. Функциональные особенности и пользовательский интерфейс данного приложения были разработаны в результате анализа существующих решений в области каталогизации информационных ресурсов различных типов, в том числе и пространственных. Созданное веб-приложение в полной мере поддерживает используемую в основе каталога пространственных данных фасетную классификацию, предоставляя пользователям достаточно широкие возможности поиска и фильтрации ресурсов, создание персональных наборов геоданных, средства веб-визуализации (рис. V.13).
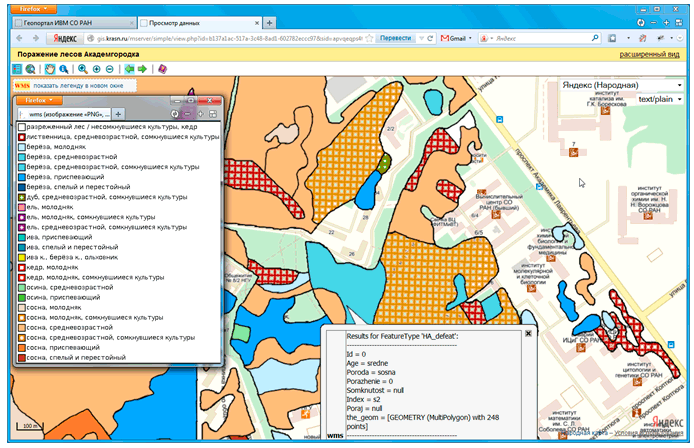
Рис. V.13. Интеграция пространственных данных на геопортале ИВМ СО РАН через протокол WMS: слой «Поражение лесов Академгородка» с сервера ИВТ СО РАН отображается на фоне подложки — «Народной Яндекс.Карты»; при этом обеспечивается корректная трансляция запросов к атрибутивным данным по объектам слоя
Основные публикации:
- Якубайлик О. Э., Гостева А. А., Ерунова М. Г., Кадочников А. А., Матвеев А. Г., Пятаев А. С., Токарев А. В.
Разработка средств информационной поддержки наблюдений за состоянием окружающей природной среды // Вестник КемГУ, 2012. — № 3/1 (51). — С. 136–142 . - Кадочников А. А., Токарев А. В.
Разработка информационной системы «Сеть образовательных учреждений Красноярского края». // Информационные ресурсы России, 2012. — № 4. — С. 29-33.
(Отдел вычислительной физики)
| К началу | |