| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2013 год
Проекты СО РАН
- Программа сибирского отделения РАН «Телекоммуникационные и мультимедийные ресурсы СО РАН»
- Программа сибирского отделения РАН «Высокопроизводительные вычисления СО РАН»
- Междисциплинарные интеграционные проекты
- Проект № 21. «Исследование закономерностей и тенденций развития самоорганизующихся систем на примере веб-пространства и биологических сообществ»
- Проект № 44. «Геометрические и алгебраические методы нахождения точных решений уравнений математической физики и механики сплошных сред»
- Проект № 49. «Разработка и исследование методов компьютерного моделирования и обработки данных для информационно-управляющих систем поддержки принятия решений по повышению уровня пожарной безопасности зданий»
- Проект № 56. «Прогнозное моделирование и междисциплинарные комплексные исследования многолетней динамики состояния экосистем меромектических озер Сибири»
- Проект № 71. «Магнитные эффекты в биологически значимых системах»
- Проект № 116. «Микро- и наноразмерные многофазные неизотермические течения»
- Проект № 130. «Математические модели, численные методы и параллельные алгоритмы для решения больших задач СО РАН и их реализация на многопроцессоргых суперЭВМ»
- Проект № 131. «Математическое и геоинформационное моделирование в задачах мониторинга окружающей среды и поддержка принятия решений на основе данных стационарного, мобильного и дистанционного наблюдения»
- Проекты СО РАН, выполняемые совместно со сторонними научными организациями
- Экспедиционные проекты СО РАН
Междисциплинарные интеграционные проекты
Проект № 21. «Исследование закономерностей и тенденций развития самоорганизующихся систем на примере веб-пространства и биологических сообществ»
Руководитель проекта: член-корреспондент РАН А. М. Федотов
Ответственный исполнитель ИВМ СО РАН: д.т.н., профессор Л. Ф. Ноженкова
Исполнители: А. В. Коробко, Т. Г. Пенькова, С. В. Исаев, Д. Д. Кононов, М. Г. Садовский, М. Ю. Сенашова
1. Концептуальная OLAP-модель веб-пространства научного сообщества Красноярского края.
На основе интеграции технологии оперативной аналитической обработки данных и анализа формальных концептов разработан метод построения концептуальной аналитической модели предметной области в виде решетки многомерных кубов. Предложенный метод заключается в применении анализа формальных концептов к объектам OLAP: показателям и измерениям и содержит следующие этапы: формирование множества объектов анализа предметной области; построение формального контекста; определение формальных кубов-концептов; построение концептуальной решетки OLAP-кубов.
На первом этапе определяются объекты анализа, используемые для построения OLAP-кубов концептуальной модели путем исследования аналитических задач предметной области. В соответствии с моделью многомерного представления данных, объекты анализа делятся на множество показателей F = {f1, f2, ..., fm} и множество измерений D = {d1, d2, ..., dn}. Термины, определяющие аспекты анализа предметной области, образуют множество измерений, а термины, представляющие количественные характеристики анализируемого процесса, образуют множество показателей.
На втором этапе на множестве всех объектов анализа формируется формальный контекст. Он определяется как тройка K = (F, D, R), где F — множество показателей, D — множество измерений, R — отношение сопоставимости между элементами множеств F и D, характеризующее возможность совместной аналитической обработки показателей и измерений.
На третьем этапе на основе формального контекста K определяется множество кубов-концептов (OLAP-кубов) по признаку сопоставимости объектов анализа. Пара (A, B), где $A \subseteq F$, $B \subseteq D$ называется кубом-концептом контекста K. Множество A состоит из показателей одинаковой размерности, которые могут быть проанализированы по всем измерениям из B. (A, B) — многомерный куб, полный относительно добавления показателей той же размерности и состава измерений. Это означает, что невозможно включить в такой OLAP-куб дополнительный показатель, без уменьшения числа измерений, то есть в рамках построенного формального контекста не существует других показателей, сопоставимых с тем же набором измерений. Множество показателей A представляет объем куба-концепта, а множество измерений B — содержание куба-концепта.
На четвертом этапе формируется решетка многомерных кубов. Множество всех кубов-концептов частично упорядочено отношением Галуа: (A1, B1) ≤ (A2, B2), если $A1 \subseteq A2$ и $B2 \subseteq B1$. В этом случае (A1, B1) — подкуб (A2, B2), а (A2, B2) — надкуб (A1, B1). Упорядоченное отношением подкуб-надкуб множество всех кубов-концептов образует концептуальную решетку OLAP-кубов, которая представляет собой интегральную OLAP-модель предметной области. Интегральная модель охватывает максимальное количество аналитических задач и дает возможность оперировать всеми объектами анализа предметной области одновременно.
На основе данных мониторинга научно-образовательных ресурсов выполнено построение контекста (рис. V.4) и концептуальной решетки (рис. V.5) веб-пространства научного сообщества Красноярского края.
Определены следующие множества объектов анализа: элементы множества F = {количество организаций, количество сайтов, количество страниц, количество версий страницы, посещаемость страницы, количество ресурсов, количество ссылок, количество добавленных страниц, количество добавленных ресурсов, количество добавленных ссылок} и элементы множества D = {организация, тип организации, научное направление, домен, страна, сайт, страница, статус страницы, статус версии, тип ресурса, тип ссылки, дата, период}. Концептуальная аналитическая модель веб-пространства научного сообщества согласно построенному контексту содержит 13 концептов. Исследование смежных областей позволит постепенно наращивать количество объектов анализа, менять объем и содержание концептов. Свойства концептуальной решетки позволяют выявлять нестандартные аналитические зависимости на множестве всех объектов анализа предметной области.
2. Автоматизация сбора контента научно-образовательных сайтов Красноярского края.
Осуществлялся мониторинг веб-пространства научно-образовательных ресурсов Красноярского края. Выявлена тенденция к уменьшению числа веб-сайтов. Созданы единовременные копии сайтов, с помощью которых определены некоторые количественные характеристики, такие как объем, количество страниц, количество документов, количество изображений. Данные приведены в таблице V.2.
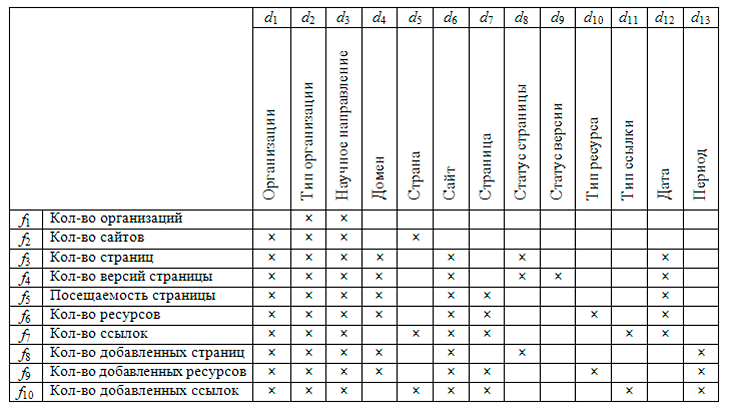
Рис. V.4. Формальный контекст веб-пространства научного сообщества
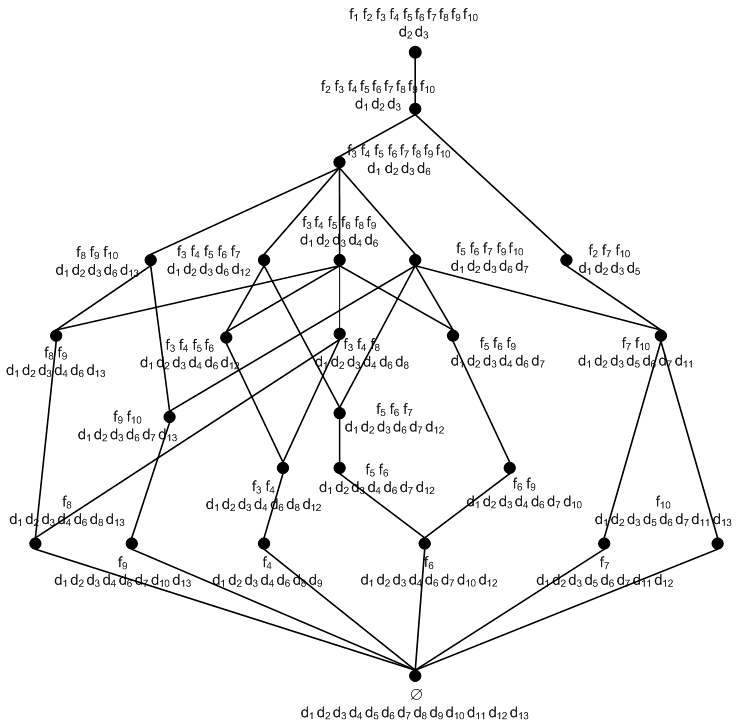
Рис. V.5. Концептуальная решетка веб-пространства научного сообщества
| Наименование организации | Веб-сайт | Объем на 10.2013 в МБ | Страниц | Документов (pdf, doc, zip) | Изображений (jpg, png, gif) |
|---|---|---|---|---|---|
| Восточно-Сибирский институт туризма | vsit.ru | 133 | 206 | 39 | 1122 |
| Государственная универсальная научная библиотека Красноярского края | www.kraslib.ru | 6200 | 82122 | 417 | 6919 |
| Институт биофизики | www.ibp.ru | 65 | 345 | 169 | 510 |
| Институт вычислительного моделирования СО РАН | icm.krasn.ru | 4600 | 47576 | 6576 | 623 |
| Институт леса | forest.akadem.ru | 672 | 600 | 780 | 948 |
| Институт медицинских проблем Севера СО РАМН | www.impn.ru | 208 | 225 | 179 | 125 |
| Институт педагогики и психологии развития СО РАО | www.ippd.ru | 209 | 3014 | 0 | 2213 |
| Институт физики | kirensky.ru | 3348 | 48635 | 416 | 2133 |
| Институт химии | www.icct.ru | 88 | 19 | 0 | 26 |
| Красноярская государственная академия музыки и театра | www.kgamit.ru | 311 | 397 | 88 | 253 |
| Красноярский государственный аграрный университет | www.kgau.ru | 1102 | 1661 | 2136 | 2229 |
| Красноярский государственный медицинский университет имени профессора В. Ф. Войно-Ясенецкого | www.krasgmu.ru | 1325 | 8104 | 371 | 8626 |
| Красноярский государственный педагогический университет имени В. П. Астафьева | www.kspu.ru | 5220 | 12580 | 4168 | 12336 |
| Красноярский государственный художественный институт | www.kghi.ru (в 2013 году недоступен) | 0 | 0 | 0 | 0 |
| Красноярский институт экономики НОУ ВПО «Санкт-Петербургский университет управления и экономики» | www.krkime.com | 15 | 987 | 0 | 75 |
| Красноярский научно-исследовательский институт геологии и минерального сырья | www.kniigims.ru (в 2013 году недоступен) | 0 | 0 | 0 | 0 |
| Красноярский научный центр СО РАН | ksc.krasn.ru | 578 | 66 | 62 | 1404 |
| КрасноярскПромСтройНИИпроект | www.psnp.ru | 247 | 249 | 161 | 375 |
| НИИ сельского хозяйства РАСХН | sorashn.ru | 749 | 6159 | 423 | 7135 |
| Сибирский государственный аэрокосмический университет имени академика М. Ф. Решетнёва | www.sibsau.ru | 3672 | 80366 | 0 | 375 |
| Сибирский государственный технологический университет | www.sibstu.kts.ru | 1473 | 2189 | 1045 | 1330 |
| Сибирский институт бизнеса, управления и психологии | www.sibup.ru | 102 | 998 | 59 | 18 |
| Сибирский научно-исследовательский и проектный институт цветной металлургии | www.sibmetproekt.ru | 24 | 106 | 31 | 119 |
| Сибирский федеральный университет | www.sfu-kras.ru | 3041 | 23841 | 441 | 11176 |
| Сибирский юридический институт | www.sibli.ru | 891 | 15988 | 0 | 1520 |
| СКТБ НАУКА | www.sktb-nauka.ru | 7 | 272 | 0 | 2 |
| ЦКБ «Геофизика» | www.geockb.ru | 28 | 161 | 1 | 361 |
Таблица V.2. Основные количественные характеристики научно-образовательных ресурсов Красноярского края
Реализованы параллельные алгоритмы обхода сайтов на основе модели гипервизора (hypervisor). Гипервизор управляет обработчиками (workers), осуществляя их запуск, остановку и контроль выполнения заданий. Созданы дополнительные структуры данных и реализованы алгоритмы управления и обработки очередей страниц. Реализованы методы снижения нагрузки на веб-сервера при обходе сайтов сообщества.
Временные срезы осуществляются посредством создания снимков сайтов. Снимок включает набор сайтов со страницами и ссылками, зафиксированный на определенный момент времени. Снимок включает полную карту связности страниц сайтов в рамках заданного сообщества. Имеется возможность запуска построения снимков исследуемого сообщества.
Реализованы алгоритмы обработки страниц сайтов с вычленением метаинформации и ключевых слов. Полученная информация может быть использована для семантического анализа страниц. Сохранение версий страниц сопровождается их привязкой к снимкам. При сохранении содержимого страниц используется принцип дедупликации (deduplication) — технология повторного использования объектов, имеющих одинаковое содержимое.
За счёт используемых алгоритмов и структур данных обеспечивается возможность отслеживания динамики изменения страниц сайта и связей между страницами и сайтами. Полученные данные сохраняются в базе данных в виде связного ориентированного графа.
Алгоритмы реализованы в виде отдельных модулей, что позволяет осуществить их повторное использование, а также повышает гибкость системы при добавлении новых функций. Реализация выполнена на языке PHP с использованием библиотек CURL, PDO, PCRE, phpQuery. В качестве СУБД для хранения данных используется Postgresql.
Дополнительно выполнено создание и организационное оформление открытого информационного ресурса — электронного архива публикаций сотрудников Института. Собраны в иерархическую структуру и привязаны к описательным метаданным электронные документы — публикации сотрудников за 20
3. Модели пространственно распределённых систем различной природы (биологических, социальных, генетических) на основе принципов эволюционной оптимальности.
Для изучения динамики популяций пространственно распределенных сообществ с оптимизационной миграцией создан набор моделей для популяций, состоящих из двух видов, связанных отношениями типа «хищник-жертва», и для популяции, состоящей из одного вида. Для вышеуказанных популяций рассмотрены различные уровни информированности: глобальная и локальная информированность. Модели динамики для популяций с локальной информированностью имеют пороговый характер: при достижении некоторого критического значения численности популяции миграционное поведение особей меняется. Для построенных моделей изучены типичные предельные динамические режимы, рассмотрены некоторые фазовые портреты, описывающие типичное поведение моделей в разных областях значений параметров.
Созданы модели связи «структура-таксономия» для геномов бактерий, выявлены характерные особенности структуры многомерных данных, характеризующих эти геномы (как частоты олигонуклеотидов, так и значения информационной ёмкости частотных словарей толщины от 2 до 20), показано, что методы нелинейной статистики (метод упругих карт), а также методы линейной кластеризации (метод динамических ядер) устойчиво выделяют характерные группы геномов, близкие друг к другу в указанных пространствах. Показано, что состав данных кластеров с точки зрения таксономией носителей соответствующих геномов очень сильно неслучаен и соответствует общим правилам (морфологической) классификации биологических объектов. Аналогичные модели простроены для ряда геномов дрожжей, а также для большого набора геномов вирусов и геномов митохондрий.
Изучена стратификация избирателей России по признакам электорального поведения. Кластеры, разделяющие избирателей на классы в соответствии с таким поведение, были определены с помощью метода динамических ядер и упругих карт. Были рассмотрены факторы, влияющие на электоральное поведение избирателей. Проведено сравнительное изучение семантики политических рекламных материалов для задачи повышения эффективности их восприятия на примере особенностей восприятия агитационных рекламных материалов предвыборных кампаний различного уровня.
Основные публикации:
- Penkova T., Korobko A.
Constructing the Integral OLAP-Model for Scientific Activities Based on FCA // Knowledge Engineering, Machine Learning and Lattice Computing with Applications. Lecture Notes in Computer Science, 2013. — Vol. 7828. — P. 163–170 . - Коробко А. В., Пенькова Т. Г.
Представление и применение знаний о кубах-концептах для поддержки адаптивного манипулирования объектами анализа OLAP // Вестник СибГАУ, 2013. — № 3(49). — С. 51-57. - Mirkhes E. M., Sadovsky M. G.
New Structure in Genomes Manifests in Triplet Distribution Alongside a Sequence // Proc. IWBBIO 2013, Granada, Spain, 2013. — P. 89-97. - Sadovskii M. G., Senashova M. Yu.
Local information access may cause a chaos in migration // J. of Siberian Federal University. Mathematics and Physics, 2013. — Vol. 6. — № 1. — P. 105–113 .
(Отделы Прикладной информатики, Информационно-телекоммуникационных технологий, Вычислительной математики)
| К началу | |
Проект № 44. «Геометрические и алгебраические методы нахождения точных решений уравнений математической физики и механики сплошных сред»
№ гос. регистрации 01201255325
Руководитель проекта: академик РАН И. А. Тайманов, член-корреспондент РАН А. П. Чупахин, д.ф.-м.н. В. К. Андреев
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., профессор В. К. Андреев
Исполнители: И. В. Степанова, А. А. Родионов, Д. А. Краснова
1. Проведена групповая классификация уравнений трехмерных движений идеальной жидкости в координатах Лагранжа, когда за основные неизвестные взяты траектории и потенциал Вебера. Эта система имеет вид
\[M^{*} x_{t} =\nabla \varphi +u_{0} (\xi ),\, \, \, \, \, \, \, \det M=1,~~~~~~~~(V.1)\]
где $M={\partial (x)\mathord{\left/ {\vphantom {\partial (x) \partial (\xi )}} \right.} \partial (\xi )} $ — матрица Якоби, $\textit{M}$* — транспонированная к ней матрица, $u_{0} (\xi )$ — начальное поле скоростей и $div{\rm \; }u_{0} =0.$
Преобразования эквивалентности для системы (V.1): а) все преобразования переменных $\xi $, сохраняющие объем; б) замена потенциала Вебера $\varphi $ на функцию $\varphi +a_{1} \xi +a_{2} \eta +a_{3} \zeta, $ $a_{j} ={\rm const.}$ Оказалось, что базис основной алгебры Ли системы (V.1) индуцируется частью алгебры Ли системы уравнений Эйлера в координатах вектор скорости-давление (исключаются операторы растяжения). Анализ показал, что классифицирующие уравнения содержат только компоненты начальной завихренности $\omega ={\rm rot}_{\xi } u_{0} (\xi ).$ Найдены все расширения основной алгебры, когда $\omega \equiv {\rm const;}$
\[\begin{array}{l} {\; \xi \cdot \nabla \omega ^{k} +\eta \cdot \nabla \omega ^{k} -\nabla \eta ^{k} \cdot \omega =0,\, \, \, \, \, \, k\; =\; {\rm 1},{\rm 2},{\rm 3};\, \, \, \, \, \, \eta \cdot \nabla \omega ^{k} +\omega ^{k} -\nabla \eta ^{k} \cdot \omega =0;} \, \, \, \, \, \, {\eta \cdot \nabla \omega ^{k} -\nabla \eta ^{k} \cdot \omega =0,} \end{array}~~~~~~~~(V.2)\]
где $\omega ^{k}$ — компоненты $\omega $, а $\eta ^{k} (\xi )$ — координаты инфинитезимального оператора при $\partial \xi, $ $\partial \eta, $ $\partial \zeta, $ соответственно. Дополнительно решена задача о допускаемой группе Ли системы (V.1), когда начальные условия $x=\xi, {\rm \; }y=\eta, {\rm \; }z=\zeta, {\rm \; }\varphi =0,{\rm \; }t=0{\rm \; }$ инвариантны. Выделены все случаи специализаций начальной завихренности, при которых возможно расширение основной алгебры Ли (В. К. Андреев, Д. А. Краснова).
2. Исследованы групповые свойства гидростатической модели движения идеальной жидкости в поле силы тяжести, когда $p_{z} =-g,$ где $\textit{z}$ — вертикальная координата. Найдена основная алгебра Ли этой системы. Построены стационарные решения, описывающие, в частности, волновые течения. Доказано, что в данной модели при рассмотрении волновых движений производная от давления по внешней нормали к волне всегда строго отрицательна и задача Коши-Пуассона корректно поставлена в классах функций конечной гладкости. Установлено, что в координатах Лагранжа трехмерная задача сводится к отысканию только двух неизвестных функций — траектории в горизонтальной плоскости; проекция же траектории на вертикальную ось находится в явном виде. Построены новые точные нестационарные решения в случае линейной зависимости вертикальной скорости от координаты — это инвариантные решения на двумерной подалгебре (В. К. Андреев, А. А. Родионов).
3. Рассматриваются уравнения тепломассопереноса при отсутствии движения с учетом эффекта термодиффузии
\[T_{t} =\chi (T_{xx} +T_{yy} +T_{zz} )+\frac{\partial \chi }{\partial T} \left(T_{x}^{2} +T_{y}^{2} +T_{z}^{2} \right)+\frac{\partial \chi }{\partial C} \left(T_{x} C_{x} +T_{y} C_{y} +T_{z} C_{z} \right) \] \[C_{t} =D(C_{xx} +C_{yy} +C_{zz} )+\frac{\partial D}{\partial T} \left(T_{x} C_{x} +T_{y} C_{y} +T_{z} C_{z} \right)+\frac{\partial D}{\partial C} \left(C_{x}^{2} +C_{y}^{2} +C_{z}^{2} \right)+~~~~~~~~(V.3)\] \[+D^{\theta } (T_{xx} +T_{yy} +T_{zz} )+\frac{\partial D^{\theta } }{\partial T} \left(T_{x}^{2} +T_{y}^{2} +T_{z}^{2} \right)+\frac{\partial D^{\theta } }{\partial C} \left(T_{x} C_{x} +T_{y} C_{y} +T_{z} C_{z} \right).\]
Коэффициенты температуропроводности $\; \chi, $ диффузии $\textit{D}$ и термодиффузии $\textit{D${}^{\theta }$}$ считаются функциями отклонений температуры $\textit{T}$ и концентрации $\textit{C}$ от их средних постоянных значений $\textit{T}{}_{0}$ и $\textit{C}{}_{0}$. Относительно данных коэффициентов переноса решена задача групповой классификации: найдены аналитические представления данных параметров и дифференциальные операторы, допускаемые системой (V.3) при каждом конкретном виде классифицируемых функций. Вычислена основная алгебра операторов, допускаемых системой при произвольных значениях искомых коэффициентов:
\[L_{0} =\left\langle \partial _{t} ,\, \, \partial _{x} ,\, \, \partial _{y} ,\, \, \partial _{z} ,\, \, 2t\partial _{t} +x\partial _{x} +y\partial _{y} +z\partial _{z} ,\, \, \, y\partial _{x} -x\partial _{y} ,\, \, z\partial _{x} -x\partial _{z} ,\, \, z\partial _{y} -y\partial _{z} \right\rangle . \]
Данная алгебра не содержит произвольных функций и, следовательно, является конечномерной, что является достаточно редкой особенностью для моделей, описывающих физические процессы.
Непосредственными вычислениями было показано, что когда коэффициент температуропроводности $\chi $ существенно зависит от концентрации $C$, то решение задачи групповой классификации уравнений (V.3) совпадает с решением аналогичной задачи для полных уравнений конвективного тепломассопереноса, если в последних положить компоненты скорости равными нулю. Решение задачи в двумерном случае представлено в таблице V.3.
В первом и втором столбцах даны аналитические зависимости искомых функций $\chi $, $\textit{D}$, $\textit{D${}_{\theta }$}$ от параметров $\textit{T}$ и $\textit{C}$. Операторы, допускаемые системой (V.3) в каждом из случаев, представлены в третьем столбце. Аргумент $w$ произвольных гладких ненулевых функций $f_{j}, \, \, \, j=2,3,4$, выписан в последнем столбце таблицы. Постоянные $\textit{l}$, $\textit{h}$, $\textit{k}$, $\textit{m}$, $\textit{n}$ и $\textit{q}$ — произвольные, причем такие, что $l\ne 0,\, \, h\ne 1$.
Обозначения операторов, представленных в таблице V.3:
\[Z_{3} =(m-n)t\partial _{t} +(m-n)x\partial _{x} +(m-n)y\partial _{y} ,\]
\[T^{1} =T\partial _{T} ,\, \, T^{3} =\partial _{T} ,\, \, C^{1} =C\partial _{C} ,\, \, C^{2} =T\partial _{C} ,\, \, C^{3} =\partial _{C} .\, \]
Оператор $\textit{Z}{}_{3}$ соответствует группе растяжений, операторы $\textit{T}{}^{1}$, $\textit{C}{}^{1}$, $\textit{T}{}^{3}$, $\textit{C}{}^{3}$ отражают инвариантность температуры и концентрации по отношению к преобразованиям сдвига и растяжения. Оператор $\textit{C}$${}^{2}$ порождает преобразование переменных, позволяющее привести уравнения на температуру и концентрацию в системе (V.3) к одинаковой дифференциальной структуре.
Из табл. V.3 видно, что коэффициенты переноса могут быть представлены степенными и экспоненциальными зависимостями от параметров состояния. Следует отметить, что классификация проведена с точностью до произвольных функций $f_{j} =f_{j} (w),\, \, \, j=2,3,4$, что позволяет более точно подобрать зависимость, аппроксимирующую экспериментальные данные.
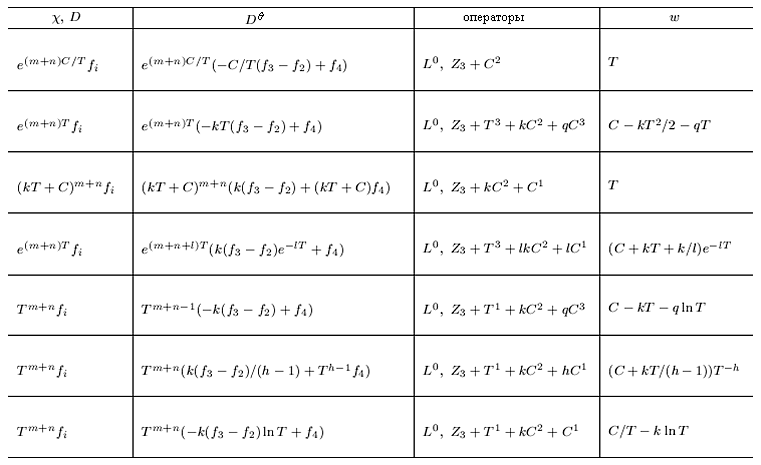
Таблица V.3
На основе полученных результатов построены точные решения системы (V.3). Пусть в процессе тепломассопереноса в плоском слое функции температуры и концентрации зависят только от поперечной координаты $\textit{y}$, коэффициенты переноса зависят только от температуры. На твердых стенках ставятся условия отсутствия потока вещества, и задается средняя концентрация в слое. При постоянных значениях коэффициента температуропроводности задача сводится к решению уравнений
\[\chi T_{yy} =0,\, \, \, \, \, DC_{yy} +\frac{\partial D}{\partial T} T_{y} C_{y} +D^{\theta } T_{yy} +\frac{\partial D^{\theta } }{\partial T} T_{y}^{2} =0~~~~~~~~(V.4)\]
с граничными условиями
\[y=0:\, \, \, T=T_{0} -\frac{\Delta T}{2} ,\, \, \, \, \, \, DC_{y} +D^{\theta } T_{y} =0, \] \[y=L:\, \, \, T=T_{0} +\frac{\Delta T}{2} ,\, \, \, \, \, \, DC_{y} +D^{\theta } T_{y} =0~~~~~~~(V.5)\]
и дополнительным условием
\[\frac{1}{L} \int _{0}^{L}C(y)dy=\tilde{N}_{0},~~~~~~~~(V.6)\]
где $\textit{L}$ — ширина слоя, $\Delta T$ — разность температур.
Задача (V.4)−(V.6) решена в случае зависимости коэффициентов диффузии и термодиффузии от температуры по квадратичному закону:
\[D=D_{0} (1+\alpha (T-T_{0} )^{2} ),\, \, \, \, \, \, \, \, \, \, \, \, \, S_{T} =S_{T0} (1+\beta (T-T_{0} )^{2} ),~~~~~~~~~(V.7)\]
где $S_{T} =D^{\theta } C_{0} (1-C_{0} )/D$ — параметр Соре, $D_{0}, \, \, \, S_{T0}, \, \, \alpha, \, \, \beta $ — постоянные коэффициенты. При $\alpha \to 0,\, \, \, \beta \to 0$ коэффициенты переноса являются постоянными и зависимость $\textit{C}$ от $\textit{y}$ линейна, как в стандартной модели Обербека-Буссинеска. На рис. V.6 показаны распределения функции, отвечающей отклонениям концентрации: кривая 1 построена при $\alpha \to 0$, т.е. для постоянного коэффициента диффузии и переменного параметра Соре, кривая 2 — при $\, \beta \to 0$, т.е. для переменного коэффициента диффузии и постоянного параметра Соре, кривая 3 — для общего случая, учитывающего зависимости (V.7).
Из рисунка видно, что существенные отличия начинают проявляться при достаточно больших $\textit{y}$, при малых значениях продольной координаты зависимость C от $\textit{y}$ близка к линейной. Тем самым учет переменных коэффициентов переноса важен для описания течений в достаточно протяженных по высоте каналах (И. В. Степанова).
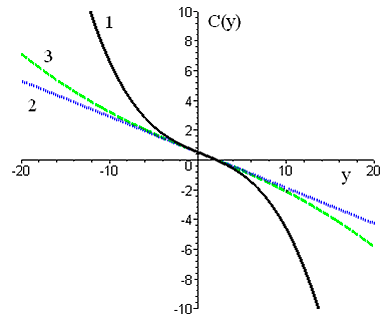
Рис. V.6. Профили концентрации при различных зависимостях коэффициентов переноса
Основные публикации:
- Stepanova I. V.
Group classification for equations of thermodiffusion in binary mixture // Communications in Nonlinear Science and Numerical Simulation, 2013. — Vol. 18(6). — P. 1341–134 6. - Андреев В. К., Степанова И. В.
Обобщение решения Обербека -Буссинеска уравнений конвекции для нелинейной силы плавучести // Тез. докл. междунар. конф. «Дифференциальные уравнения. Функциональные пространства. Теория приближений». — Новосибирск: ИМ СО РАН, 2013. — С. 80. - Андреев В. К.
Симметрии уравнений двумерных движений жидкости в переменных траектории-потенциал Вебера // Материалы LXVI Междунар. научной конф. «Герценовские чтения — 2013». — СПб: РГПУ, 2013. — С. 18-23.
(Отдел дифференциальных уравнений механики)
| К началу | |
Проект № 49. «Разработка и исследование методов компьютерного моделирования и обработки данных для информационно-управляющих систем поддержки принятия решений по повышению уровня пожарной безопасности зданий»
№ гос. регистрации 01201268795
Руководитель проекта: член-корреспондент РАН В. В. Шайдуров
Ответственный исполнитель ИВМ СО РАН: д.т.н., проф. Л. Ф. Ноженкова
Исполнители: А. А. Евсюков, Е. С. Кирик, Р. В. Морозов
1. Выполнена автоматизация пространственного и временного OLAP-GIS анализа рассчитанных данных по эвакуации и распространению ОФП.
Разработано методическое и программное обеспечение для автоматизации пространственного и временного анализа рассчитанных данных по эвакуации и распространению опасных факторов пожара (ОФП), основанное на применении технологий оперативной аналитической обработки данных (OLAP) и технологии геоинформационного моделирования (GIS).
С помощью программного блока аналитической обработки данных формируются отчеты о процессе эвакуации людей, о блокировании эвакуационных путей, о попадании эвакуируемых в зоны с предельно допустимыми значениями опасных факторов пожара. Строятся сравнительные таблицы времен эвакуации и стадий развития пожара для выявления опасности воздействия опасных факторов пожара на людей.
Создан виртуальный тренажер пожарной безопасности. Предусмотрен режим виртуальной эвакуации от третьего лица: камера трехмерной сцены следует за анимированной моделью человека, управляемой пользователем.
Выполнено проектирование продукционной базы знаний на основе оценки рисков и моделирования последствий воздействия опасных факторов. На основе базы знаний формируются управляющие рекомендации по снижению пожарного риска: первая группа мероприятий направлена на повышение эффективности работы систем противопожарной защиты, вторая группа — на сокращение времени эвакуации, третья группа — на увеличение времени блокирования эвакуационных путей, на ограничение распространения пожара и его опасных факторов.
Выполнен анализ динамических свойств полевой модели движения людей.
На данном этапе получены результаты тестирования динамических свойств разрабатываемой модели движения людей, реализуемые на прямых участках путей.
Тест 1. Анализ свойств модели при переформировании потока в части растекания и уплотнения. Для проверки этих свойств вычислительный эксперимент проводится при открытых граничных условиях. В качестве тестовой геометрии рассматриваются два прямых коридора шириной 2 м и длиной 50 и 100 м соответственно. Люди в начальный момент времени равномерно располагаются на первых 50-ти метрах. Вычислительный эксперимент проводится при различных начальных плотностях.
В реальной жизни растекание потока возникает вследствие стремления людей двигаться в условиях комфортной плотности. Этот факт также обусловлен возможностью фронтальной части потока двигаться с большей скоростью. При наличии свободного места на путях движения это явление реализуется. Вычислительный эксперимент с двумя коридорами позволяет проверить реализацию этого явления.
Динамика потока измеряется средними удельными потоками $J_{s} ^{50} =N/\tilde{T}^{50} /2$ и $J_{s} ^{100} =N/\tilde{T}^{100} /2$ для коридоров 50 и 100 м соответственно, где $\tilde{T}_{}^{50} =T_{tot}^{50}, [s]$ — среднее время эвакуации $N$ человек из коридора 50 м, $\tilde{T}_{}^{100} =T_{tot}^{100} -t_{v^{0} }, {\rm \; \; }[s]$ — среднее время эвакуации $N$ человек из коридора 100 м без учета времени добегания фронтальной части до контрольного сечения ($t_{v^{0} } $).
Численно растекание выражается в том, что удельный поток для коридора 100 м ниже, чем для коридора 50 м при плотностях, начиная с 0.5 чел/м2. Доказательством является динамика значений удельного потока с увеличением начальной плотности. В случае 50-метрового коридора места для разуплотнения нет, плотность потока на контрольном сечении остается примерно равной начальной плотности. За счет этого величина потока стремится к предельной пропускной способности сечения, что выражается в стабилизации значения потока (удельного потока) с ростом начальной плотности. Для случая 100-метрового коридора величина потока имеет тенденцию к росту с изменением начальной плотности — за счет разуплотнения интенсивность движения такова, что не достигается поток, соответствующий предельной пропускной способности. В итоге увеличение начальной плотности ведет к постоянному росту удельного потока.
На рис. V.7 представлены результаты вычислительного эксперимента. Из графиков видно, что реализуются ожидаемые явления, что свидетельствует о воспроизведении моделью свойства растекания потока.
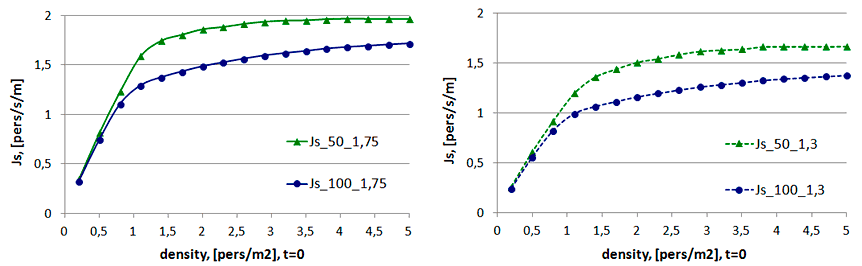
Рис. V.7. Средний удельный поток, чел/с/м, в зависимости от начальной плотности, чел/м2, для эксперимента с открытыми граничными условиями для коридоров 50 и 100 м, средняя скорость свободного движения: справа — 1.3 м/с, слева — 1.75 м/с
Тест 2. Анализ свойств модели при поддержании скорости свободного движения до достижения критического значения локальной плотности. Экспериментально было показано, что до определенного значения локальной плотности движущиеся люди не мешают друг другу и тем самым не влияют на скорость «соседей». Экспериментально установленными критическими значениями плотности следует считать 0.5-0.6 чел/м2.
При всех прочих равных условиях наличие дополнительного места в такой ситуации не должно приводить к растеканию потока. При тестировании модели показано (рис. V.7), что средние удельные потоки $J_{s} ^{50} $ и $J_{s} ^{100} $ для коридоров 50 м и 100 м соответственно совпадают на участке малых плотностей — до 0.5-0.6 чел/м${}^{2}$, причем эти значения плотности согласуются с натурными наблюдениями. С учетом способа вычисления времени эвакуации для коридора 100 м (см. тест 1) это свидетельствует о том, что для таких плотностей не происходит переформирование (растекание) потока в коридоре длины 100 м. В этом случае и для 50-метрового, и для 100-метрового коридоров в потоке поддерживается начальная плотность в течение всего эксперимента; люди двигаются со скоростью свободного движения.
Тест 3. зависимость скорости от локальной плотности (выполнение свойств фундаментальной диаграммы). Экспериментально было показано, что скорость движения человека контролируется локальной плотностью потока: скорость убывает с увеличением плотности. Качественно эта зависимость описывается так: до достижения определенного значения локальной плотности величина удельного потока растет, затем начинает уменьшаться. Частично это явление демонстрируют результаты, описанные в тесте 1. Свободная фронтальная часть движется с большей скоростью, чем средняя и хвостовая.
Другой эксперимент, на котором можно проверить выполнение этого свойства в модели, состоит в моделировании движения в периодических граничных условиях. Это условие означает, что в области моделирования поддерживается постоянная плотность. Движение организовано в прямом коридоре шириной 2 м.
Если модель поддерживает зависимость скорости движения потока от плотности, это должно выражаться в среднем равномерном распределении людей по области моделирования и в среднем одинаковой скорости движения.
Удельный поток для моделей индивидуально-поточного типа подсчитывается на основании следующих данных: для каждой плотности определяется время $\textit{T}$ прохождения $\textit{N}$ человек (например, $\textit{N=1000}$) через контрольное сечение, по серии из 100 экспериментов определяется наиболее вероятное значение времени. Удельный поток в контрольном сечении рассчитывается по формуле $\textit{J${}_{мод }$= N/T/2 }$чел./с/м.
Результаты вычислительного эксперимента представлены на рис. V.8. Сравнение модельных данных с данными натурных экспериментов позволяет констатировать, что модельные данные укладываются в современную концепцию зависимости скоростного режима потока людей от текущей локальной плотности.
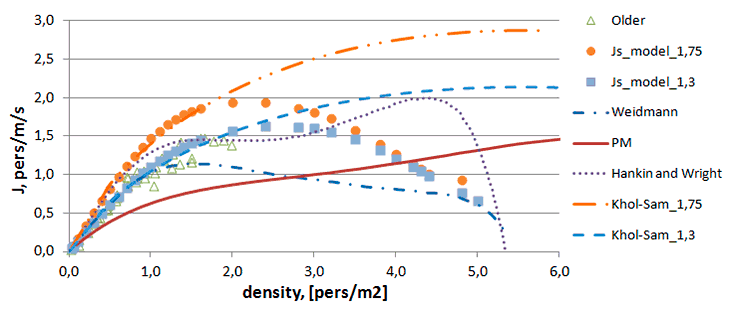
Рис. V.8. Фундаментальные диаграммы в контрольном сечении для эксперимента с периодичными граничными условиями: модельные кривые удельных потоков для скоростей свободного движения 1.75 м/с и 1.3 м/с; удельные потоки, полученные разными авторами в натурных экспериментах в схожих условиях
Проводя более детальный анализ, отметим, что модельные кривые для обеих скоростей практически совпадают с соответствующими экспериментальными данными. Совпадение происходит для малых и средних значений плотности вплоть до 2-2.5 чел/м2. Этот диапазон плотностей является «рабочим» при решении подавляющего числа задач по расчету времени эвакуации. Плотности свыше 2.2 чел/м2 считаются травмоопасными и не соответствуют нормальному режиму эвакуации.
Основные публикации:
- Кирик Е. С., Дектерев А. А., Литвинцев К. Ю., Харламов Е. Б., Малышев А. В.
Математическое моделирование эвакуации при пожаре // Математическое моделирование, 2014. — Т. 26 (1) (в печати). - Евсюков А. А., Морозов Р. В.
Виртуальный 3D-тренажер эвакуации людей при пожарах // Информатизация и связь, 2013. — № 2. — С. 49-52. - Морозов Р. В.
Создание продукционной базы знаний для оценки состояния пожарной безопасности на объектах сферы образования // Тр. V Междунар. конф. «Системный анализ и информационные технологии» (САИТ 2013). — Красноярск: ИВМ СО РАН, 2013. — C. 253–258 .
(Отделы Прикладной информатики, Информационно-телекоммуникационных технологий, Вычислительной механики деформируемых сред)
| К началу | |
Проект № 56. «Прогнозное моделирование и междисциплинарные комплексные исследования многолетней динамики состояния экосистем меромектических озер Сибири»
Руководитель проекта: академик РАН А. Г. Дегерменджи
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. В. М. Белолипецкий
Исполнители: В. М. Белолипецкий, Л. А. Компаниец, С. Н. Генова, Т. В. Якубайлик, П. В. Белолипецкий
Многолетняя динамика вертикальной термохалинной структуры озера Шира.
Выполнена модификация одномерной в вертикальном направлении модели температурного и солевого режимов озера [Genova S. N., Belolipetskii V. M., Rogozin D. Y., Degermendszhi A. G. A one-dimensional model of vertical stratification of Lake Shira focussed on winter conditions and ice cover // Aquat Ecol, 2010. 44. P. 5
В зимний период по вертикали выделяются слой льда, слой конвективного перемешивания и придонный слой. Для определения динамики толщины ледяного покрова применяется упрощенная модель, основанная на квазистационарном температурном режиме в затвердевшей области. В соленых озерах при образовании льда в результате кристаллизации воды высвобождается соль и формируется слой конвективного перемешивания. Так как в зимний период температура воды мало изменяется по глубине, то плотность воды в основном зависит от солености. С учетом этого предположения выведены расчетные формулы для определения глубины распространения конвекции и значений температуры, солености, плотности воды в конвективном слое в зимний период.
Выполнена серия расчетов динамики вертикальных распределений температуры и солености воды в озере Шира для разных лет. Результаты расчетов согласуются с данными натурных измерений.
Известные данные для озера Шира показывают, что за более чем столетний период глубина озера изменялась в пределах от 17 до 24 м [Кривошеев А. С., Хасанов А. П. Лечебные озера Красноярского края. (1990). Красноярское книжное издательство. Красноярск. 142 с.]. На рис. V.9 показаны измеренные глубины в озере за период 20
Выполнены расчеты динамики вертикальных распределений температуры и солености воды в озере Шира с учетом уменьшения и увеличения глубины. На рис. V.10 показаны изменения измеренных и рассчитанных профилей солености воды (с начальными значениями 11.07.2002 г.).
Модельные расчеты для случая уменьшения глубины озера на 60 см (за два года) показывают, что слой конвективного перемешивания зимой распространяется до дна (рис. V.11а), при этом летом соленость в гиполимнионе увеличивается (рис. V. 11б).
Одномерная модель позволяет оценить динамику вертикальных распределений температуры и солености воды озера в зависимости от метеоусловий, определить положения термоклина, халоклина и пикноклина, прогнозировать возможные перемешивания поверхностных и придонных слоев при уменьшении глубины.
Пространственно-временная изменчивость гидрофизических характеристик озера Шира. Натурные наблюдения.
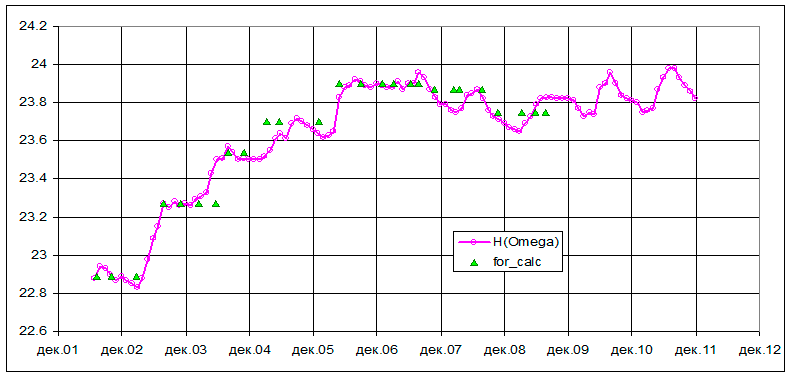
Рис. V.9. Глубина озера Шира согласно измеренным уровням (сплошная линия) и используемые уровни в модельных расчетах (треугольные маркеры)
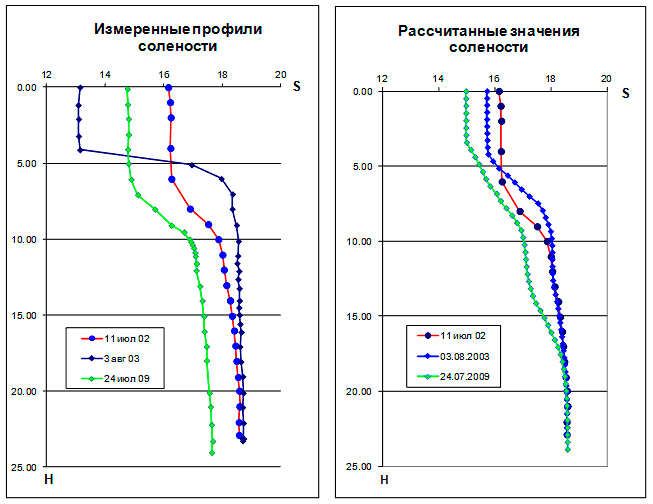
Рис. V.10. Динамика солености воды оз. Шира (натурные данные и рассчитанные профили с начальными значениями 11.07.2002 г.)
Обработаны результаты измерений основных гидрологических параметров озера Шира наблюдений 20
Обработаны результаты измерения величины и направления скорости течения в центральной точке озера, позволяющие сделать вывод о наличии горизонтальных циркуляций в озере (рис. V.13).
Обработаны результаты измерения колебания интегральной температуры (ИТ) водяного столба в фиксированной точке, предположительно обусловленные колебаниями термоклина, иллюстрирующие возможные типы внутренних волн (ВВ) в центральной части озера Шира (рис. V.14).
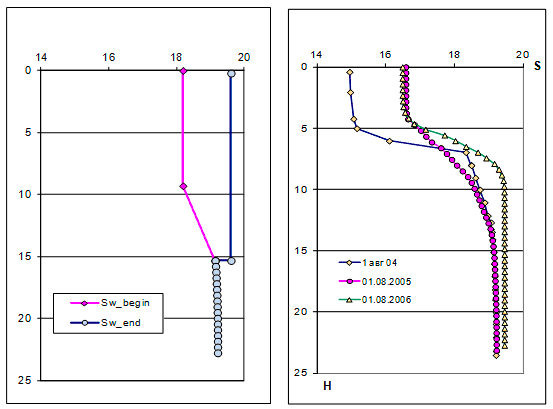
Рис. V.11. Расчет изменения солености по глубине при уменьшении глубины: а) профили солености в начале (Sw_begin) и в конце зимы (Sw_end); б) — профили солености летом
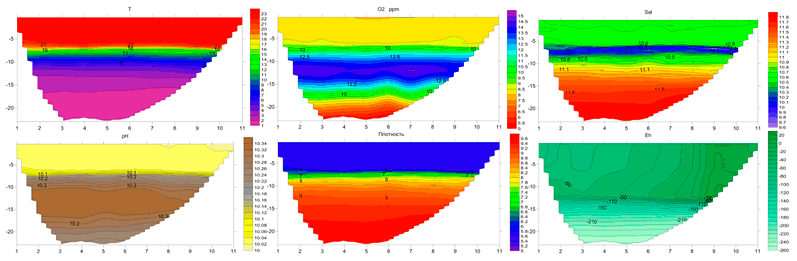
Рис. V.12. Гидрологический разрез в озере Шира 05.08.2012 г.
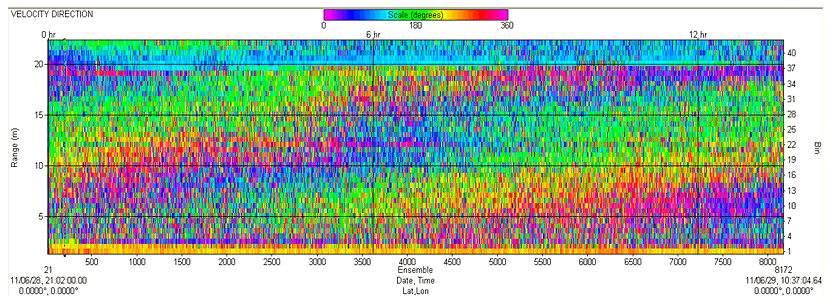
Рис. V.13. Наблюдаемый угол поворота горизонтальной скорости в центральной точке озера
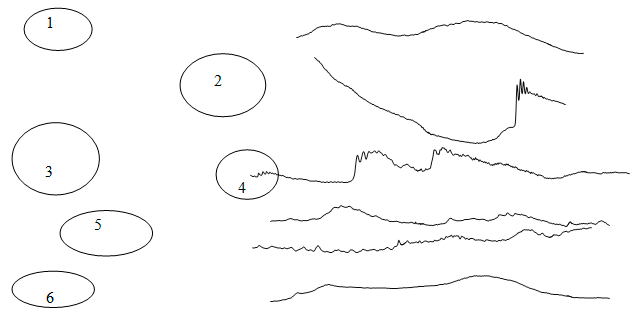
Рис. V.14. Возможные варианты формы внутренней волны в озере Шира
На рис. V.14 отмечены следующие особенности (см. пронумерованные кружки). Каждый участок занимает 4 часа.
1, 4, 6 — участки низкой активности короткопериодных ВВ.
2, 3 — резкий скачок ИТ, и вслед за ним — цуг короткопериодных ВВ. Можно предположить прохождение ударной волны (гидроудар).
5 — участок короткопериодных ВВ, возникшей предположительно после предшествующих когерентных движений (одиночных волн).
Основные публикации:
- Баранов В. И., Голенко Н. Н., Компаниец Л. А., Пака В. Т., Якубайлик Т. В.
Пространственно-временная изменчивость основных характеристик озера Шира в сезоне 2911–201 2 гг. // Вестник Бурятского гос. ун-та. Математика, Информатика, 2013. — № 9. — С. 148–156 . - Якубайлик Т. В., Компаниец Л. А.
Трехмерная численная модель исследования ветровых течений в озере Шира на основе пакета GETM. // Тез. докл. междунар. науч. конф. «Методы создания, исследования и идентификации математических моделей». — Новосибирск, 2013 — С. 104. - Белолипецкий В. М., Генова С. Н., Дегерменджи А. Г., Рогозин Д. Ю.
Многолетняя динамика вертикальной термоклинной структуры озера Шира // Тез. докл. междунар. науч. конф. «Методы создания, исследования и идентификации математических моделей». — Новосибирск, 2013. — С. 19.
(Отдел Вычислительных моделей в гидрофизике)
| К началу | |
Проект № 71. «Магнитные эффекты в биологически значимых системах»
№ гос. регистрации 01201259038
Руководители проекта: академик РАН Ю. Н. Молин
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., профессор В. М. Садовский
Совместно с Международным томографическим центром СО РАН разработан вычислительный алгоритм и компьютерная программа решения двумерного уравнения Лиувилля для матрицы плотности столкновительной пары радикалов с учетом зависимости диполь-дипольного и обменного взаимодействия спинов от расстояния между радикалами, спиновой релаксации и сверхтонкого взаимодействия неспаренных спинов электронов с магнитными ядрами радикалов. На основе этой программы проведены расчеты магнитных эффектов в рекомбинации липидных радикалов, диффундирующих по поверхности клеточных мембран. Задача актуальна для понимания механизма опосредуемых радикалами магнитных эффектов в биологических мембранах, в частности, механизма перекисного окисления липидов.
Предполагалось, что радикалы рекомбинируют только из синглетного спинового состояния и что синглет-триплетные переходы в радикальной паре обусловлены разницей $g$ — факторов, спиновой релаксацией, а также межспиновым диполь-дипольным и обменным взаимодействием и сверхтонким взаимодействием электронных спинов с магнитными ядрами. Было показано, что кинетический коэффициент рекомбинации $K(t)$ определяется через решение уравнения Лиувилля для парной матрицы плотности радикалов $\stackrel{\frown}{\rho }(r,t)$:
\[\frac{\partial \stackrel{\frown}{\rho }}{\partial t} =\stackrel{\frown}{L}\; \stackrel{\frown}{\rho }-\stackrel{\frown}{W}\cdot \stackrel{\frown}{\rho }+\stackrel{\frown}{Q}\cdot \stackrel{\frown}{\rho }.\]
Здесь $\stackrel{\frown}{L}$ — дифференциальный оператор диффузионного движения, $\stackrel{\frown}{W}$ — оператор рекомбинации радикальной пары из синглетного состояния, $\stackrel{\frown}{Q}$ — оператор, описывающий сверхтонкое взаимодействие в каждом из радикалов и зеемановское взаимодействие спинов с внешним магнитным полем. В расчетах рассматривался случай контактной рекомбинации радикальной пары, когда реакция рекомбинации происходит не дистанционно, а только при контакте радикалов. В этом случае начальное значение матрицы плотности задается формулой: $\stackrel{\frown}{\rho }(r,0)={\stackrel{\frown}{P}_{S} \, \delta (r)\mathord{\left/ {\vphantom {\stackrel{\frown}{P}_{S} \, \delta (r) 4}} \right. } 4}$, где $\stackrel{\frown}{P}_{S} $ — проектор на синглетное состояние, а $\delta (r)$ — функция Дирака.
Вычислительная особенность задачи, связанная с бесконечной областью решения, была устранена с помощью метода инверсии, который приводит в данном случае к параболическому уравнению на конечной области, вырождающемуся на границе. Дельта-функция в начальном условии при построении алгоритма аппроксимировалась в соответствии с определением обобщенных функций. Верификация алгоритма и программы осуществлялась на тестах — точных решениях уравнения.
На рис. V.15 представлена расчетная зависимость магнитного эффекта от времени при разных временах спиновой релаксации $T$. Графики показывают сильную зависимость стационарного магнитного эффекта (при t → ∞) от $T$.
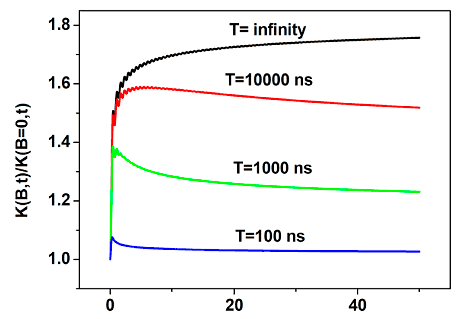
Рис. V.15. Зависимость магнитного эффекта в коэффициенте скорости от времени реакции при различных временах спиновой релаксации
Расчеты также показали сильную зависимость амплитуды магнитного эффекта в кинетическом коэффициенте от скорости спиновой релаксации как для случая, когда основным механизмом синглет-триплетной конверсии является $\Delta g$ — механизм, так и для случая, когда эта конверсия полностью определяется сверхтонким взаимодействием.
Созданная ранее в рамках интеграционного проекта компьютерная программа для расчета времен релаксации спинового эхо в магнитно-резонансной томографии на основе метода производящих функций, развитого в Международном томографическом центре, применялась для совершенствования методики измерений. Было показано, что при низком уровне шума в эксперименте по спиновому эхо, можно однозначно и с хорошей точностью восстановить времена $T_{1} $ и $T_{2} $ релаксации, используя измерения лишь одной эхо последовательности с углом рефокусировки, отличным от 180°, а не двух, как это делается в стандартных МРТ (МТЦ СО РАН, ИВМ СО РАН).
Рассматривался достаточно сложный, вырожденный случай, когда $T_{1} $ и $T_{2} $ близки между собой. В эксперименте, проведенном в лаборатории И. В. Коптюга (МТЦ СО РАН), использовался угол рефокусирующего импульса, равный 45°, в отличие от стандартных 180-градусных импульсов. В двух дополнительных экспериментах по стандартной методике для исследуемого раствора были найдены экспериментальные значения $T_{1} $ и $T_{2} $, равные 21 ± 2 мс и 21.3 ± 0.1 мс. По измерениям эхо-последовательностей первого эксперимента с помощью компьютерной программы были рассчитаны времена релаксации, которые оказались близкими к экспериментальным (рис. V.16).
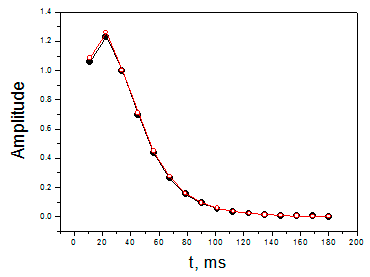
Рис. V.16. Экспериментальные (красный) и расчетные (черный) амплитуды спинового эхо
Таким образом, показано, что точность восстановления времен релаксации с использованием одной эхо-последовательности с рефокусирующим углом, отличным от 180° (что соответствует более комфортным условиям для исследуемого объекта), можно считать приемлемой.
Основные публикации:
- Лукзен Н. Н., Иванов К. Л., Садовский В. М., Каптейн Р., Сагдеев Р. З.
Магнитные и спиновые эффекты в рекомбинации радикалов на двумерной поверхности // Докл. Академии наук. 2013. Т. 449, № 3. С. 309–312 . DOI: 10.7868/S0869565213090168. Режим доступа: http://dx.doi.org/10.7868/S0869565213090168. - Lukzen N. N., Ivanov K. L., Sadovsky V. M., Kaptein R., Sagdeev R. Z.
Magnetic Field and Spin Effects on the Recombination of Radicals on Two-Dimensional Surfaces // Doklady Physical Chemistry. 2013. V. 449, Part 1. P. 44-47. DOI: 10.1134/S0012501613030056, ISSN: 1608–312 1 (online). Режим доступа: http://link.springer.com/article/10.1134%2FS0012501613030056. - Садовский В. М., Садовская О. В.
Об акустическом приближении термомеханической модели жидкого кристалла // Физическая мезомеханика, 2013. — Т. 16. — № 3. — С. 55-62.
(Отдел вычислительной механики деформируемых сред)
| К началу | |
Проект № 116. «Микро- и наноразмерные многофазные неизотермические течения»
Руководитель проекта: член-корреспондент РАН С. В. Алексеенко
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. В. К. Андреев
Исполнители: В. Б. Бекежанова, М. В. Ефимова
1. В задаче о совместном течении жидкой пленки и спутного потока газа (рис. V.17) на основе математической модели с полным энергетическим условием на поверхности раздела исследовано влияние термокапиллярных сил на характер возникающих неустойчивостей.
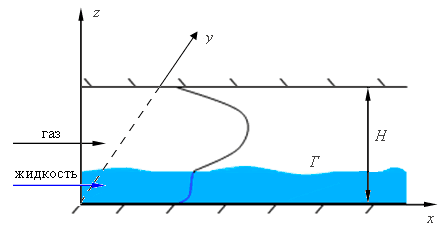
Рис. V.17. Схема течения
В качестве энергетического условия на поверхности раздела жидкость-газ используется полное условие
\[k_{g} \frac{\partial T_{g} }{\partial n} (x,h(x))-k_{l} \frac{\partial T_{l} }{\partial n} (x,h(x))=\kappa T\nabla _{11} \cdot v,~~~~~~~(V.7)\]
где выражение в правой части описывает энергию, затраченную на деформацию поверхности раздела термокапиллярными силами. Анализ условия (V.7) показал, что приращения внутренней энергии межфазной поверхности, сопряженные с поглощением или высвобождением тепла, связаны только с локальными изменениями ее площади. Значимость процесса высвобождения/поглощения теплоты при локальных изменениях площади межфазной поверхности для развития конвективного движения вблизи поверхности раздела характеризуется отношением $S=S_{M} /S_{v} $, где $S_{M}, \, S_{v} $ — характерные величины напряжений Марангони и вязких напряжений соответственно. Для пленочного течения порядок параметра $\textit{S}$ сравним с порядком других значимых критериев.
Изучено влияние приращений поверхностной внутренней энергии на тип неустойчивостей пленочного течения. Для этого решены две задачи о течении пленки, увлекаемой потоком газа: в первой задаче (задача 1) в качестве энергетического условия использовалось условие (V.7), во второй (задача 2) — классическое условие
\[k_{g} \frac{\partial T_{g} }{\partial n} \, \, =\, \, k_{l} \frac{\partial T_{l} }{\partial n}.~~~~~~~~~(V.8)\]
Оказалось, что в обеих задачах наиболее опасной является термокапиллярная мода. При этом неустойчивость проявляется в форме продольных валов, оси которых параллельны направлению основного течения (зона неустойчивости I на рис. V.18). На основе карты возможных режимов неустойчивости (рис. V.18) рассчитаны закритичные режимы, возникающие в областях II и III, демонстрирующие различия в поведении системы.
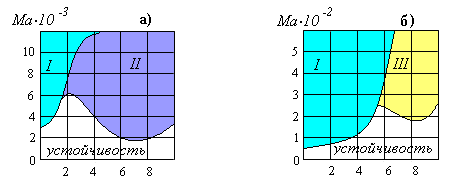
Рис. V.18. Нейтральные кривые линейной устойчивости: а) задача 1; б) задача 2
В области II кризис течения сопровождается формированием поперечных бегущих волн, которые распространяются в противоположном основному течению направлении (рис. V.19).
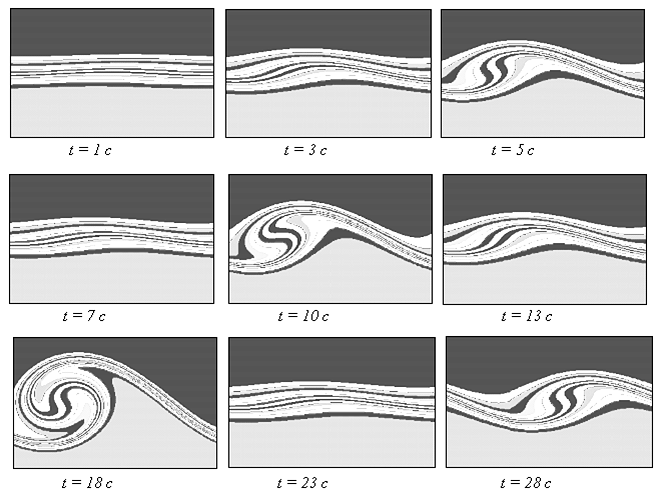
Рис. V.19. Формирование поперечных бегущих волн в задаче 1
В зоне неустойчивости II наблюдается сосуществование продольных валов, индуцируемых силами Марангони, и бегущих поперечных волн.
В задаче 2 неустойчивость в области III проявляется в виде поперечных стоячих тепловых волн (рис. V.20).

Рис. V.20. Формирование поперечной стоячей волны в задаче 2
Таким образом, градиенты сил межфазного натяжения, возникающие под влиянием теплоты, поглощаемой или выделяющейся при локальных изменениях площади межфазной поверхности, индуцируют изменение фазовой скорости волн и способствуют формированию волновых режимов. Учет дополнительного слагаемого в условии (V.7) позволил получить результат, качественно совпадающий с результатами эксперимента для системы FC-72 (жидкость) — азот (газ) (В. Б. Бекежанова).
2. Рассмотрена задача об однонаправленном движении бинарной смеси и вязкой теплопроводной жидкости с общей поверхностью раздела в системе плоских слоев, ограниченных двумя твердыми стенками. Движение жидких сред описывается уравнениями Навье — Стокса, конвективного тепло- и массообмена. На твердых стенках заданы условия прилипания, температуры и отсутствия потоков вещества через одну из них. На поверхности раздела выполнены кинематическое и динамическое условия, равенство скоростей, температур и потоков тепла, а также предполагается отсутствие потока вещества через поверхность раздела; задана линейная зависимость поверхностного натяжения от температуры и концентрации. Источником движения являются градиенты давления в слоях и термоконцентрационные эффекты на поверхности раздела. При заданных условиях найдено точное решение стационарной задачи.
На основе численного анализа обнаружено, что с ростом времени функции скорости и температуры выходят на стационарный режим. Показано, что стационарное распределение концентрации в слое с бинарной смесью имеет место лишь при отсутствии ее градиента в направлении движения. Для исследования устойчивости стационарного течения в случае недеформируемой поверхности раздела выписаны уравнения малых возмущений. Решение полученной задачи исследовалось относительно нормальных возмущений. При условии, что возмущения не зависят от времени, выписана спектральная задача относительно числа Марангони.
На рис. V.21 приведены нейтральные кривые для стационарных возмущений системы этанол — вода и бензол с параметрами $\textit{$\chi$} = 1.104$, $\textit{$\nu$} = 2.965$, $\textit{$\rho$} = 1.104$, $l={l_{1} \mathord{\left/ {\vphantom {l_{1} l_{2} }} \right.} l_{2} }$, где $\textit{l}{}_{1}$ — толщина слоя бинарной смеси, $\textit{l}{}_{2}$ — толщина слоя вязкой теплопроводной жидкости. Положительные значения числа Марангони определяют нагрев твердых стенок вдоль направления движения. В этом случае устойчивость относительно длинноволновых возмущений будет наблюдаться для системы, где $l_{1} \lt l{}_{2}$. Соответственно отрицательные значения чисел Марангони говорят об охлаждении твердых стенок вдоль направления движения. В этом случае система будет устойчивой в широком диапазоне длин волн. Если толщина слоев одинакова (l = 1), то система будет устойчивой для случая охлаждения твердых стенок вдоль направления движения (М. В. Ефимова).
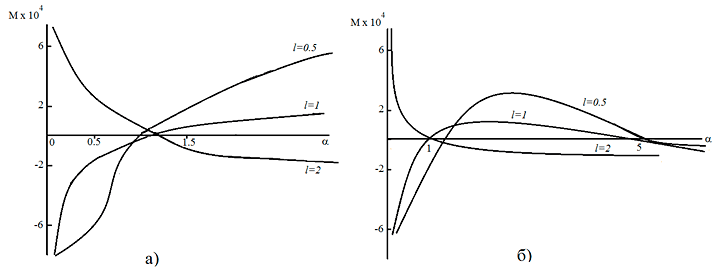
Рис. V.21. Нейтральные кривые для стационарных возмущений
Основные публикации:
- Bekezhanova V. B., Kabov O. A.
Effect of internal energy changes of the interface on the film flow stability // Book of Abstracts of the Int. Topical Team Workshop on Two-Phase Systems for Ground and Space Applications. Universitat Bremen, 2013. — P. 18-19. - Ефимова М. В.
Совместное движение бинарной смеси и вязкой теплопроводной жидкости под действием термоконцентра-ционных сил // Вычислительные технологии, 2013. — Т. 18. — № 3. — С. 4-12. - Ефимова М. В.
Об устойчивости совместного стационарного течения бинарной смеси и вязкой теплопроводной жидкости // Сб. тр. конф. «Информационно-вычислительные технологии и математическое моделирование», Кемерово, Россия, 23-30 июня 2013 г., КемГУ [Электронный ресурс], № гос. регистрации — 0321302759.
(Отдел дифференциальных уравнений механики)
| К началу | |
Проект № 130. «Математические модели, численные методы и параллельные алгоритмы для решения больших задач СО РАН и их реализация на многопроцессоргых суперЭВМ»
Руководитель проекта: академик РАН Б. Г. Михайленко
Ответственный исполнитель от ИВМ СО РАН: к.ф.-м.н., доцент Е. Д. Карепова
Исполнители: В. В. Шайдуров, Е. В. Дементьева
Для осредненных по глубине уравнений приливной динамики рассмотрена обратная задача на восстановление граничной функции, описывающей влияние океана на открытую границу вычислительной области с использованием данных наблюдений за возвышением свободной поверхности. На каждом шаге по времени ищется решение задачи, которое на границе в смысле наименьших квадратов наиболее хорошо приближает данные наблюдений. Поскольку обратная задача является некорректно поставленной, то рассмотрено несколько вариантов регуляризаторов функционала, которые берутся в виде норм восстанавливаемой функции в пространствах $L_{2}$, $H^{1}$, $H^{1/2}$.
При численном моделировании используется метод конечных элементов (МКЭ) с линейными треугольными конечными элементами на неструктурированной согласованной триангуляции акватории.
Наиболее вычислительноемкой операцией в МКЭ является сборка невязки на основе локальных матриц жесткости элементов. Существует, по крайней мере, два способа обхода триангуляции при сборке:
1) по элементам (традиционный способ, реализующий наиболее выгодное распределение памяти при хранении информации о триангуляции);
2) по точкам сетки (требует размещения в памяти дополнительных, в общем случае, нерегулярных структур, отвечающих за хранение информации о триангуляции).
Целью этапа 2013 года было исследование эффективности нескольких возможных параллельных реализаций МКЭ для решения задачи на SMP-узловых кластерах. Расчеты проводились на высокопроизводительных комплексах СФУ и ССКЦ СО РАН. Перечислим основные выводы, которые можно сделать на основе теоретического и численного анализа (рис. V.22).
1. Последовательные реализации. Численные эксперименты показали, что время выполнения последовательной программы при сборке невязки по элементам в 1.5 раза меньше, чем при сборке по точкам сетки.
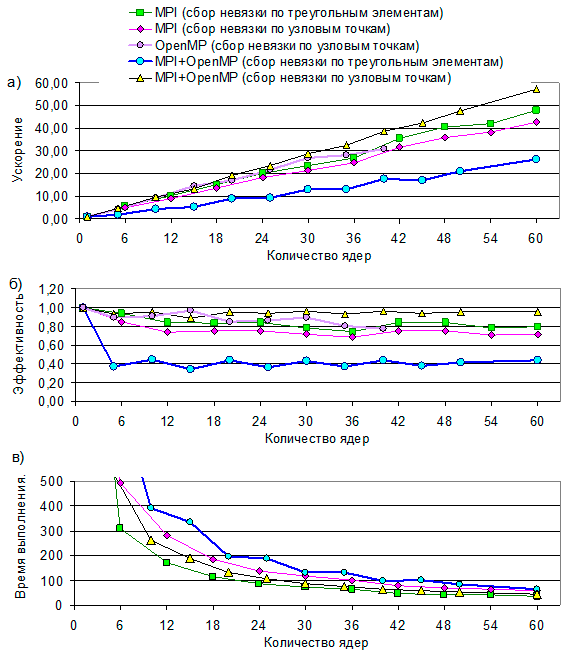
Рис. V.22. Анализ эффективности нескольких параллельных реализаций МКЭ для задачи о граничной функции для уравнений приливной динамики
2. Реализации для вычислительных систем (ВС) с общей памятью на основе технологии OpenMP. Поскольку вклад в невязку в точке дают несколько треугольников, то при параллельной реализации поэлементной сборки на общей памяти будут существовать точки сетки, которые обрабатываются разными нитями, причем, возможно, одновременно. Следовательно, в этом случае необходимы дополнительные затраты на синхронизацию нитей, которая занимает до 40% времени выполнения основного цикла: эффективность распараллеливания около 25%. При сборке невязки по точкам сетки дополнительной синхронизации нитей не требуется, что дает явные преимущества этого подхода. Эффективность распараллеливания составляет около 90% при использовании до 30 нитей и около 80% при использовании более 30 нитей (одна нить на ядро).
3. Реализация для ВС с распределенной памятью на основе технологии MPI. Поскольку используется подход, связанный с декомпозицией вычислительной области без теневых граней, то при обоих способах сборки невязки на каждой итерации неизбежно возникают следующие накладные расходы: 1) время, затрачиваемое на обмены типа точка-точка между соседними процессами для сборки полной невязки на разрезах вычислительной области; 2) время на коллективную операцию глобальной редукции для расчета критерия останова итерационного процесса. Численные эксперименты показали преимущество сборки невязки по элементам. Особо следует отметить, что эта версия MPI-программы по времени выполнения выигрывает и по сравнению с самой быстрой OpenMP-версией.
4. Совмещение технологий MPI и OpenMP для SMP-узлового кластера (рис. V.22). Наиболее эффективной оказалась MPI+OpenMP-версия программы при сборке невязки по точкам сетки. Следует отметить, что она является наиболее сложной в реализации (требует создания, хранения и обработки дополнительных структур). Наименьшее время выполнения показывает MPI-версия со сборкой по элементам.
Основные публикации:
- Дементьева Е. В., Карепова Е. Д., Шайдуров В. В.
Восстановление граничной функции по данным наблюдений для задачи распространения поверхностных волн в акватории с открытой границей // СибЖИМ, 2013. — Т. 16. — № 1. — С. 10-20. - Karepova E., Dementyeva E.
The Numerical Solution of the Boundary Function Inverse Problem for the Tidal Models // Lecture Notes in Computer Science, 2013. — Vol. 8236. — P. 345–354 . - Дементьева Е. В., Карепова Е. Д.
Обратная задача с неизвестной граничной функцией для уравнений мелкой воды // Тр. V Междунар. конф. «Системный анализ и информационные технологии» (САИТ). — Красноярск: ИВМ СО РАН, 2013. — Т. 1. — С. 56-65.
(Отдел вычислительной математики)
| К началу | |
Проект № 131. «Математическое и геоинформационное моделирование в задачах мониторинга окружающей среды и поддержка принятия решений на основе данных стационарного, мобильного и дистанционного наблюдения»
Руководитель проекта: академик РАН Ю. И. Шокин
Ответственный исполнитель от ИВМ СО РАН: к.ф.-м.н. О. Э. Якубайлик
Исполнители: А. А. Кадочников, А. Г. Матвеев, А. С. Пятаев
Задачей и содержанием научных исследований в отчетный период времени являлось проведение углубленного анализа существующих реальных технологических цепочек получения, передачи, хранения и использования данных в задачах аппаратного мониторинга.
Анализировались соответствующие информационные модели и структуры данных для хранения и обработки геоинформации, в соответствии с требованиями, вытекающими из типовых задач мониторинга (типовых моделей наблюдений и анализа).
Функциональные возможности создаваемых информационных моделей для сопровождения регулярных наблюдений за окружающей средой связаны с созданием распределенной информационно-вычислительной системы, предназначенной для решения задач:
- сбора, интеграции и хранения данных;
- поиска метаданных, включая запросы по временным, пространственным и содержательным характеристикам;
- наполнения и предоставления данных из хранилища через веб-сервисы;
- интерактивного анализа и визуального представления данных.
Были проанализированы существующие системы экологического мониторинга, проблемы и особенности реализации технологических цепочек для получения, передачи, хранения и использования данных. Примеры сервисов сбора и обработки:
- Pachube/Cosm/Xively (http://xively.com) — сервис, позволяющий собирать, транслировать и визуализировать потоки различных данных. Пользователь системы может, к примеру, подключить термометр к сервису и транслировать температуру у вас за окном в интернет-пространство. Проект несколько раз переименовывался, менялась лицензионная политика с уклоном в коммерческую сторону.
- Народный мониторинг (http://narodmon.ru) — молодой проект по сбору и отображению на карте мира показаний различных датчиков среды (температура, давление, влажность и т.п.) практически в реальном времени по фактическому состоянию.
- OpenWeatherMap (http://openweathermap.org). Собираются данные от профессиональных и частных погодных станций (> 40 тыс.). Набор показателей фиксирован, около 15 шт, такие как: направление и скорость ветра, температура, влажность, давление, осадки, освещенность и др. На основе собранных данных делается прогноз погоды. С помощью API можно получать текущую погоду, прогноз, и исходные данные с метеостанций.
Были выполнены работы по созданию подсистемы хранения и сбора климатических данных, которая даст возможность пользователям выполнять сбор, интеграцию, хранение и анализ данных (Рис. V.22).
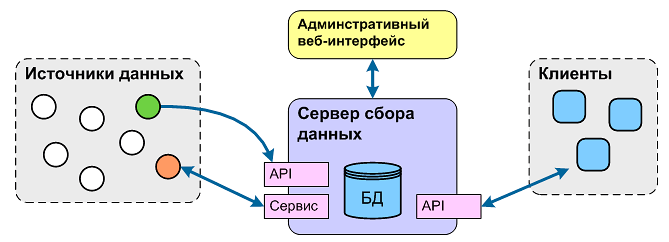
Рис. V.22. Общая архитектура системы мониторинга
Показатели с внешних источников данных собираются на сервере сбора. Источниками данных могут быть отдельные датчики, внешние базы данных или информационные системы через дополнительные адаптеры. Предусмотрено несколько способов наполнения: активного, выполняющего периодический опрос и загрузку данных из источника и пассивного, обеспечивающего только прием данных по инициативе источника через предоставленный программный интерфейс (API) в виде веб-сервиса. Извлечение данных возможно как в «сыром», так и в агрегированном по времени виде. Доступ к серверу сбора предоставляется только после аутентификации. Для этого в каждом запросе передается уникальный ключ. Поддерживается разграничение доступа в зависимости от прав пользователя. Административный веб-интерфейс содержит необходимые инструменты для управления пользователями, проектами, показателями и другими сущностями системы.
Для хранения метаинформации и собираемых данных разработана концептуальная модель базы данных (Рис. V.23).
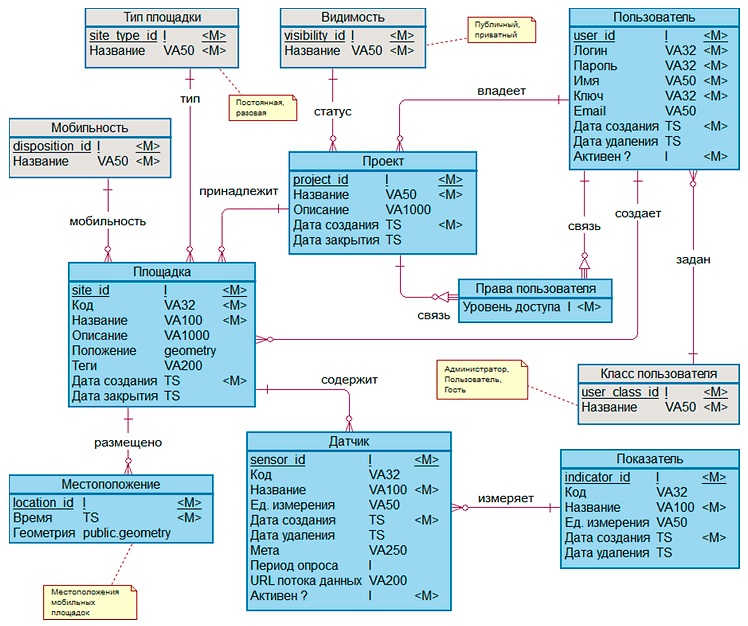
Рис. V.23. Концептуальная модель базы данных (ядро)
1. Получить описание проекта. GET http://host/1.0/projects/<project_id>/metadata.xml. Возвращается полное описание проекта и список собираемых показателей.
2. Получить площадки проекта. GET http://host/1.0/projects/<project_id>/sites.xml. Возвращается список площадок, которые зарегистрированы в проекте (Рис. V.24).

Рис. V.24. Примеры ответов веб-сервиса
3. Получить «сырые» данные измерений. GET http://host/1.0/projects/<project_id>/values.xml?<filter>. Параметры определяют дополнительные фильтры на данные:
- time_begin — дата начала выборки (YYYY-MM-DD HH:mm:ss);
- time_end — дата окончания выборки;
- extent — область выборки (xmin,ymin, xmax, ymax);
- sites — площадки (site_id, site_id, ...);
- indicators — показатели (indicator_code, indicator_code, ...);
- limit — максимальное число возвращаемых записей (по-умолчанию, 1000);
- offset — смещение в возвращаемых записях (по-умолчанию, 0);
- srid — код проекции (по-умолчанию, 4326)
- fields — список необходимых полей в возвращаемом массиве (по-умолчанию, все);
4. Получить агрегированные данные. GET http://host/1.0/projects/<project_id>/aggvalues.xml?<filter>. Параметры практически аналогичны параметрам предыдущего запроса, добавляется только: time_interval — интервал агрегации данных (1week, 1day, 1hour, 5min).
5. Отправить текущие данные. POST http://host/1.0/projects/<project_id>/current_values.xml. За один запрос можно передать текущие значения показателей для разных площадок проекта.
6. Отправить архивные данные. POST http://host/1.0/projects/<project_id>/values.xml. Функция позволяет загрузить массив данных по нескольким площадкам за прошлые периоды времени. Для каждого замера явно указывается дата-время. Если в базе уже есть данные с указанными параметрами (site, indicator, date), то они заменяются новыми.
7. Удалить массив данных. DELETE http://host/1.0/projects/<project_id>/values.xml?<filter>. Параметры аналогичны параметрам запроса на выборку данных. Удаляются все данные, попавшие в выборку.
Разработка выполнялась на языке сценариев PHP 5 с использованием фреймворка Yii. Это высокоэффективный PHP-фреймворк для разработки веб-приложений. Он основан на компонентной структуре и позволяет максимально применить концепцию повторного использования кода, существенно ускоряя процесс веб-разработки. Для хранения данных выбрана СУБД PostgreSQL с модулем расширения PostGIS, которые обеспечивают удобную работу с пространственными данными внутри СУБД.
Созданы несколько потоков данных из разных типов источников — открытых источников климатических данных, автономных метеостанций, систем мониторинга за состоянием окружающей природной среды.
Реализована простая метеостанция на основе аппаратно-вычислительной платформы Arduino. Использованы такие компоненты, как Arduino Uno, Ethernet Shield W5100, сенсор BMP085. На языке программирования Processing написана программа для микроконтроллера ATmega328, обеспечивающая опрос сенсоров и передачу данных на сервер по сети Ethernet. На текущий момент измеряется температура и атмосферное давление, в дальнейшем количество измеряемых параметров можно расширять.
Выполнена загрузка ежедневных сводок глобального покрытия от Национального климатического центра США. GSOD ежедневно пополняется данными с метеорологических стаций всего мира, в том числе — с российских метеостанций. Эти данные представляют собой отчеты, которые содержат информацию о значении температуры, влажности воздуха, скорости и направлении ветра, атмосферного давления, типах осадков и т.п.
Выполнена загрузка данных из информационной системы «ГИС мониторинга состояния окружающей природной среды в зоне действия предприятий нефтегазовой отрасли Красноярского края», где собраны результаты проведения наблюдений за 20
Ведутся работы по созданию средств эффективного доступа к данным наблюдений, сервисов представления и анализа информации. Планируется интеграция с геопорталом ИВМ СО РАН.
Основные публикации:
- Матвеев А. Г., Якубайлик О. Э.
Проектирование и разработка программно-технологического обеспечения для геопространственных веб-приложений // Фундаментальные исследования, 2013. — № 10. — Ч. 15. — С. 3358–336 2. - Матвеев А. Г., Якубайлик О. Э.
Система управления контентом геоинформационного веб-портала «Геофреймворк» // Современные проблемы науки и образования, 2013. — № 6. — URL: www.science-education.ru/113–109 97 (дата обращения: 05.12.2013).
(Отдел вычислительной физики)
| К началу | |