| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2013 год
Проекты СО РАН
- Программа сибирского отделения РАН «Телекоммуникационные и мультимедийные ресурсы СО РАН»
- Программа сибирского отделения РАН «Высокопроизводительные вычисления СО РАН»
- Междисциплинарные интеграционные проекты
- Проекты СО РАН, выполняемые совместно со сторонними научными организациями
- Проект № 38. «Фундаментальные задачи конвекции в неоднородных средах: теория, эксперимент и новые приложения»
- Проект № 73. «Современные технологии формирования информационной инфраструктуры для поддержки междисциплинарных исследований, в том числе для мониторинга природных и социальных процессов территорий Сибири и Дальнего Востока»
- Проект № 74. «Разработка принципов и информационно-вычислительных технологий обработки и интерпретации мультиспектральных спутниковых изображений высокого и сверхвысокого пространственного разрешения (для наук о Земле, экологии и природопользования)»
- Проект № 4. «Концепция устойчивого развития и природно-техногенной безопасности территорий Беларуси и Сибири, построенная на основе учета рисков и с применением геоинформационных технологий»
- Экспедиционные проекты СО РАН
Проекты СО РАН, выполняемые совместно со сторонними научными организациями
Проект № 38. «Фундаментальные задачи конвекции в неоднородных средах: теория, эксперимент и новые приложения»
№ гос. регистрации 01201255325
Руководитель проекта: член-корреспондент РАН В. В. Пухначев
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., профессор В. К. Андреев
Исполнители: В. Б. Бекежанова, М. В. Ефимова, И. И. Рыжков, И. В. Степанова, Н. Л. Собачкина, Е. Н. Лемешкова
1. Получены условия возникновения конвекции в цилиндрическом контейнере со свободной верхней границей. Пусть цилиндрический контейнер $(0,a)\times (0,2\pi )\times (-h,0)$ заполнен покоящейся жидкостью с верхней свободной деформируемой границей, на которой задан теплообмен с окружающей средой. Равновесное состояние системы в рамках модели Обербека-Буссинеска описывается формулами
\[u=0,\quad p_{z} =\rho _{o} g\beta \Theta ,\quad \Theta =Az+B,~~~~~~~~(V.9)\]
$A$, $B$ — температурные коэффициенты, которые находятся из условия на нижнем основании и условия теплового контакта на свободной границе:
\[A=\frac{{\rm Bi(}\Theta _{01} -\Theta _{02} {\rm )}}{(1+{\rm Bi})h} ,\quad B=\frac{\Theta _{01} +{\rm Bi}\Theta _{02} }{1+{\rm Bi}},~~~~~~~~(V.10)\]
${\rm Bi}$ — число Био; $\Theta _{01} $ и $\Theta _{02} $ — температуры на нижнем и верхнем основании соответственно. Поверхностное натяжение линейно зависит от температуры, а свободная граница — плоская (круг). Давление квадратично зависит от $z$ и имеет вид
\[p=\rho _{o} g\beta \left(\frac{A}{2} z^{2} +Bz\right)+c,\quad c={\rm const}.~~~~~~~~(V.11)\]
При некоторой критической разности температур на основаниях цилиндра $\Theta _{01} -\Theta _{02} $ возникает движение — конвекция. С целью определения этой разности рассматривается линеаризованная на равновесном состоянии (V.9) — (V.11) задача о малых возмущениях системы в рамках модели Обербека-Буссинеска, решение которой ищется в виде нормальных волн
\[\left(U,P,T,R\right)=\left(U\left(r,z\right),P\left(r,z\right),T\left(r,z\right),N\right)\exp \left[i\left(s\varphi -Ct\right)\right],~~~~~~~~(V.12)\]
где $P$, $T$, $U$ — возмущение основного решения $p$, $\Theta $ и $u$; $R$ — нормальная составляющая вектора возмущений на свободной границе; $N$ — отклонение амплитуды возмущений свободной границы по нормали; $s$ — азимутальное волновое число; $C$ — комплексный декремент. Тогда для осесимметричного случая $(s=0)$, монотонных возмущений $(C=0)$ в безразмерных переменных (в качестве масштаба длины, времени, скорости, давления и температуры выбраны соответственно $h$, $h^{2} /\nu $, $\nu /h$, $\rho _{o} \nu ^{2} /h^{2} $, $Ah$) задача характеризуется безразмерными параметрами $(U=(U,0,W))$ ${\rm G}=g\beta Ah^{4} /\nu ^{2} $, ${\rm G}'=g\beta Bh^{3} /\nu ^{2} $ — числа Грасгофа; ${\rm Pr}=\nu /\chi $ — число Прандтля; ${\rm We}=\sigma h/\rho _{o} \nu ^{2}$ — число Вебера; $M = \unicode{xE6} Ah^{2} /\rho _{o} \nu \chi$ — число Марангони (заметим, что в силу (V.12) оно прямо пропорционально искомой разности температур на нижнем и верхнем основании цилиндра).
Задача на возмущения допускает разделение переменных, именно
\[U=\frac{1}{r} R\left(r\right)F_{z} \left(z\right),\quad W=-\frac{1}{r} R_{r} \left(r\right)F\left(z\right),\quad T=\frac{1}{r} R_{r} \left(r\right)D\left(z\right),\]
\[R=R_{n} \left(r\right)=rJ_{1} \left(mr\right),\quad N=N_{0} r^{-1} R_{r} \left(r\right)\equiv mN_{0} J_{0} \left(m\right),\; \; N_{0} ={\rm const},\]
$m=\alpha \delta _{n} =h\delta _{n} /a$, а $\delta _{n} ,\; n=1,2...$, есть решение уравнения $J_{0} \left(\delta \right)=0$.
В результате для $D$ получим ОДУ шестого порядка $L^{3} D-m^{2} {\rm PrG}D=0,$ где $L=d^{2} /dz^{2} -m^{2} $, а функция $F(z)$ находится из уравнения $F=-{\rm Pr}^{-1} LD$. Функция $D$ определяется с точностью до шести постоянных, которые находятся из шести граничных условий. Решение уравнения для $D$ находится в явном виде и его подстановка в граничные условия дает возможность найти критические числа Марангони путём аналитических вычислений в системе Maple.
Была рассмотрена конкретная жидкость — трансформаторное масло. Физические параметры жидкости таковы: $\rho _{o} =0.86\cdot 10^{3} $ кг/м$^{3} $, $\nu =18.49\cdot 10^{-6} $ м${}^{2}$/c, $\chi =1.21\cdot 10^{-5} м{}^{2}/c$, $k=0.63519\cdot 10^{-4} $ кг м/с${}^{3}$К, $\beta =0.7\cdot 10^{-3} К^{-1}$, $\unicode{xE6} = 0.0022$ Н/мК, $\sigma =3.81\cdot 10^{-2}$ Н/м.
На рис. V.25 приведен график зависимости числа Марангони от $m=\delta _{n} h/a$ при $1\le m\le 10$. Здесь ${\rm We}=10^{4} $, ${\rm Bi}=2$. Физически это означает следующее. Например, в точке $(1.92674905565;3.203963483\cdot 10^{5} )$ график функции достигает своего минимума, и если $n=1$, т.е. $\delta _{1} =2.4048255577$, то исходя из формул для $m$ и ${\rm M}$ получим, что при таком отношении высоты слоя жидкости к радиусу цилиндра, а именно, $h/a=0.8012011722$, критическая разность температур $\Theta _{01} -\Theta _{02} =27.23325641$К. Если $n=5$ ($\delta _{5} =14.9309177086$), то данная разность температур уже будет достигаться, когда $h/a=0.1290442485$.
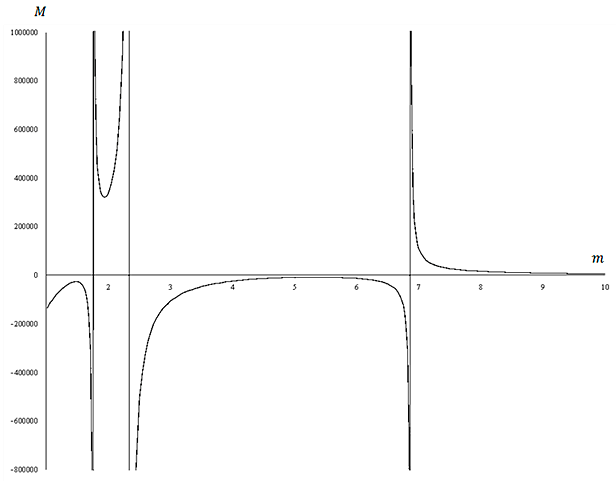
Рис. V.25. Зависимость числа Марангони от m при We = 104, Bi = 2
В случае невесомости (${\rm G}=0$, ${\rm G}'=0$) число Марангони имеет вид
\[{\rm M}=\frac{8m\left({\rm Bi}\, \sinh \, m+m\, \, \cosh \, m\right)\left(m-\sinh m\cosh m\right)}{m^{3} \cosh m-\sinh ^{3} m-8m^{3} \cosh m\mathop{\left({\rm PrWe}\right)}\nolimits^{-1} } .\]
Если $m=h\delta _{n} /a\to m_{0} ={\rm const}$ при $a\to \infty $, $n\to \infty $, то это выражение в точности совпадает с числом Марангони для бесконечного слоя (Рябицкий Е. А., 1993). График зависимости критических чисел Марангони от числа $m_{0} $ приведен на рис. V.26.
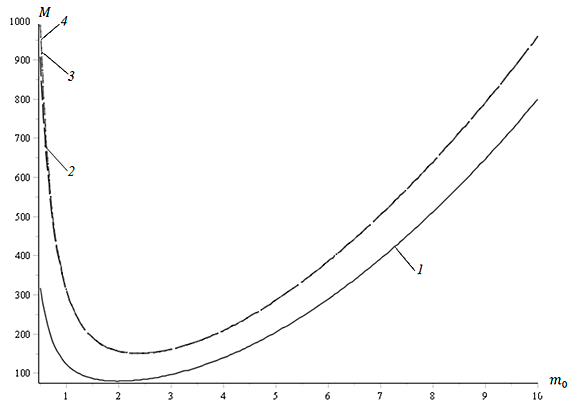
Рис. V.26. Зависимость числа Марангони от $\textit{m${}_{0}$}$ при $We = 10{}^{4}$, Bi = 2. Кривая 1: ${\rm We}=10^{4} $ и ${\rm Bi}=0$; кривая 2: ${\rm We}=10^{4} $ и ${\rm Bi}=2$; кривая 3: ${\rm We}=10^{7} $ и ${\rm Bi}=2$; кривая 4: ${\rm We}=\infty$ и ${\rm Bi}=2$.
Таблица V.4 показывает влияние чисел Вебера и коэффициента теплоотдачи Био на критическую разность температур для чисел Марангони и mo, см. кривые 1 — 4 на рис. V.26.
| кривая 1 | кривая 2 | кривая 3 | кривая 4 | |
|---|---|---|---|---|
| точка минимума | (1.99, 79.534) | (2.4, 150.614) | (2.4, 150.6844121) | (2.4, 150.6844822) |
| $h/a$ | 0.8275 | 0.998 | 0.998 | 0.998 |
| $\Theta_{01}-\Theta_{02} $ | 0.0007 К | 0.001317235403 К | 0.00131785121 К | 0.001317851824 К |
Таблица V.4
Таким образом, зная заранее геометрию контейнера и физические параметры жидкости, находящейся в нём, можно определить критическую разность температур, при которой возникнет конвекция (В. К. Андреев, Е. П. Магденко).
2. Рассмотрена система уравнений двумерных движений вязкой теплопроводной жидкости с постоянными коэффициентами переноса и в отсутствие силы тяжести. Эти уравнения допускают четырехмерную подалгебру $\left\langle \partial _{x}, t\partial _{x} +\partial _{u}, \partial _{p}, \partial _{\theta } \right\rangle, $ где $u(x,y,t)$ — компонента скорости вдоль оси x, $p(x,y,t)$ — давление, $\theta (x,y,t)$ — температура. Частично инвариантное решение ранга два и дефекта три относительно этой группы имеет вид
\[u(x,y,t)=U(y,t)x,\, \, \, \, \, \, v=V(y,t),\, \, \, \, \, \, p=P(x,y,t),\, \, \, \, \, \, \theta =T(x,y,t).~~~~~~~~~(V.13)\]
Подстановка вида решения в систему уравнений конкретизирует вид функций $\textit{P}$ и $\textit{T}$:
\[\frac{1}{\rho } P=\frac{F(t)x^{2} }{2} +\, L(y,t),\, \, \, \, \, \, T=A(y,t)x^{2} +B(y,t).~~~~~~~~~~(V.14)\]
Функции $U(y,t)$, $V(y,t)$, $L(y,t)$, $A(y,t)$, $B(y,t)$ удовлетворяют системе нелинейных уравнений 2-го порядка. Решение (V.13), (V.14) удобно интерпретировать как нестационарное двухслойное движение двух жидкостей в плоском канале с общей границей раздела $y=l(t)$, ($l(t)$ — искомый элемент задачи). Исключение функций $\textit{V${}_{j}$}$ из уравнения сохранения массы ($\textit{j} = 1,2$) и замена переменных $z={y\mathord{\left/ {\vphantom {y l(t)}} \right.} l(t)} $ для первого и $\xi ={(y-h)\mathord{\left/ {\vphantom {(y-h) [l(t)}} \right.} [l(t)} -h]$ для второго слоя ($h={\rm const}$ — общая толщина слоев) приводит к задаче для нелинейной интегродифференциальной системы уравнений уже в фиксированной области $0 \lt \textit{z} \lt 1$ и $0 \lt \textit{$\xi$} \lt 1$. Решение последней ищется $\tau$-методом, причем за базисные функции взяты смещенные полиномы Якоби. Выписана система галёркинских приближений, представляющая собой нелинейные ОДУ по временной переменной. Все граничные условия учтены в этой системе.
Для более полного понимания структуры движения предварительно была рассмотрена задача о двумерном движении вида (V.13), (V.14) без поверхности раздела. Такая задача путем введения безразмерных переменных $\tau ={\nu t\mathord{\left/ {\vphantom {\nu t h^{2}, }} \right.} h^{2}, } $ $z={y\mathord{\left/ {\vphantom {y h,}} \right.} h,} $ $W={h^{2} U\mathord{\left/ {\vphantom {h^{2} U \nu }} \right.} \nu } $ сводится к начально-краевой задаче
\[W_{\tau } -W_{z} \int _{0}^{z}W(z,\tau ) \, dz+W^{2} -W_{zz} =F(\tau )=\frac{h^{4} }{\nu ^{2} } f(t)\]
на интервале 0 < z < 1 с начальными и граничными условиями
\[\begin{array}{l} {W(z,0)=W_{0} (z),\, \, \, \, \, \, 0\le z\le 1;\, \, \, \, \, \, W(0,\tau )=W(1,\tau )=0,\, \, \, \, \, \, \, \, \tau \ge \, 0;} \ {\int _{0}^{1}W(z,\tau ) \, dz\, =0,\, \, \, \, \, \tau \ge \, 0,} \end{array}\]
причем $W_{0}(0)=W_{0}(1)=0$, $\int _{0}^{1}W_{0} (z) \, dz=0$. Отметим, что $F(\tau )$ — искомая функция наряду с $\textit{W}$.
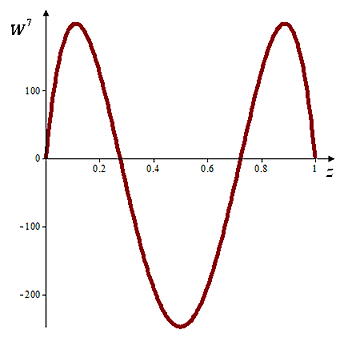
Рис. V.27. Поведение функции W при n = 7
Решение поставленной задачи искалось в виде
\[W^{n} (z,\tau )=\sum _{k=0}^{n}W^{k} (\tau )\, R_{k} (z),\, \, \]
где $R_{k} (z)=P_{k} (2z-1),\, \, $$z\in [0,1],$ — смещенные полиномы Лежандра, $P_{k} (y)\, \, $ — обычные полиномы Лежандра. Расчеты проводились для $\textit{n} = 5$ и $\textit{n} = 7$, причем решение очень быстро со временем стремится к нулевому: $\textit{W}$ = 0, $\textit{F}$ = 0.
Интересно отметить, что соответствующая стационарная задача имеет, кроме нулевого, нетривиальное решение. Для такого решения вид функции $\textit{W${}_{7}$}$ показан на рис. V.27, где $F_{cm} \approx 28859.6.$ Для воды ($\nu \approx 0.01 см{}^{2}/с$) и толщины слоя $\textit{h}$ = 1 см получим $f_{cm} ={\nu ^{2} F_{cm} \mathord{\left/ {\vphantom {\nu ^{2} F_{cm} h^{4} \approx 2.8859}} \right. } h^{4} \approx 2.8859} см{}^{2}/с$ (В. К. Андреев, Е. Н. Лемешкова).
3. Рассмотрена задача об устойчивости механического равновесия в системе из двух горизонтальных слоев (рис. V.28).
Слои образованы двумя фазами одной и той же бинарной смеси (циклогексан-метанол). Фазовая диаграмма данной смеси показана на рис. V.29. Из этой диаграммы, в частности, видно, что при температуре $T_{0} =25\, {}^{{\rm o}} {\rm C}$ слои 1 и 2 образованы фазами с массовой долей (концентрацией) циклогексана 0.95 и 0.36 соответственно (в поле силы тяжести менее плотная фаза располагается в верхнем слое). При возникновении разности температур $\Delta T$ между нижней и верхней границами слоя (рис. V.28) вертикальный градиент температуры приводит к возникновению градиентов концентрации в каждом слое благодаря эффекту Соре. Значения концентраций на границе раздела определяются согласно фазовой диаграмме и линейно зависят от температуры (рис. V.29). Закон сохранения массы компонентов смеси приводит к зависимости толщин слоев от приложенной разности температур.
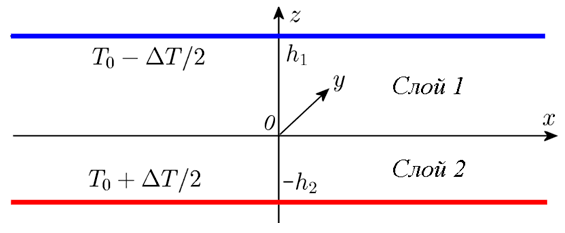
Рис. V.28. Двухслойная система
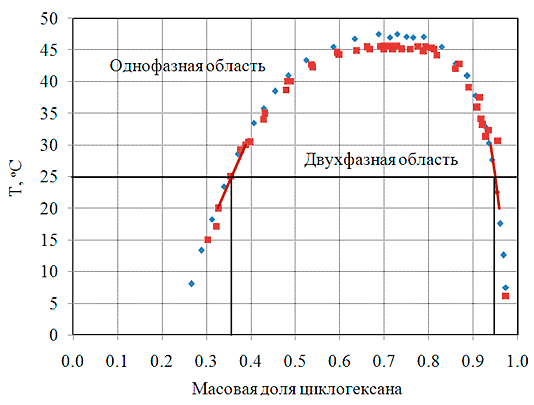
Рис. V.29. Фазовая диаграмма смеси циклогексан — метанол. Точки — экспериментальные данные, прямые линии — аппроксимация бинодали вблизи T = 25° C
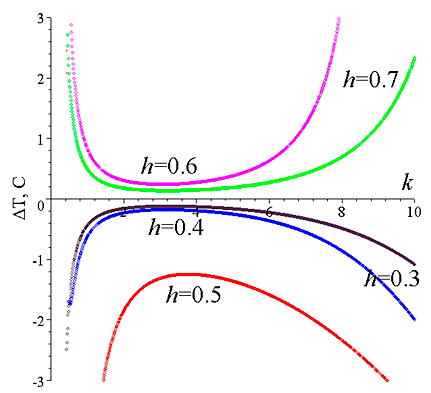
Рис. V.30. Нейтральные кривые (зависимость критической разности температур от волнового числа) для различных значений отношения $h=h_{2} (h_{1} +h_{2} )^{-1}$
Поставлена задача об устойчивости механического равновесия относительно малых возмущений в линейном приближении. Поведение смесей описываются уравнениями Навье-Стокса и тепломассопереноса с учетом эффекта Соре для каждой из фаз. Предполагается, что граница раздела является деформируемой. Основными механизмами возникновения неустойчивости в данной системе являются: 1) гравитационный, 2) термокапиллярный (межфазное натяжение зависит от температуры), 3) фазовый переход (учитывается перенос массы через границу и теплота фазового перехода).
Для случая отсутствия гравитации и монотонных возмущений найдено точное решение линеаризованных амплитудных уравнений и построены нейтральные кривые, описывающие зависимость критической разности температур от волнового числа. Эти кривые для различных значений отношения толщины второго слоя к общей толщине слоев $h=h_{2} (h_{1} +h_{2} )^{-1} $ показаны на рис. V.30.
При положительных (отрицательных) $\Delta $T система неустойчива в областях, расположенных выше (ниже) соответствующих кривых. Анализ результатов показывает, что если толщина второго слоя меньше толщины первого, то монотонная неустойчивость имеет место при подогреве сверху. В случае, когда толщина второго слоя превышает толщину первого слоя, монотонная неустойчивость имеет место при подогреве снизу. Структура критических возмущений скорости, температуры и концентрации для случая $\textit{h}$ = 0,5 показана на рис. V.31.
Для анализа общего случая монотонных и колебательных возмущений разработана программа на основе метода пошагового интегрирования с ортогонализацией с учетом зависимости толщин слоев от приложенной разности температур (И. И. Рыжков, В. К. Андреев).
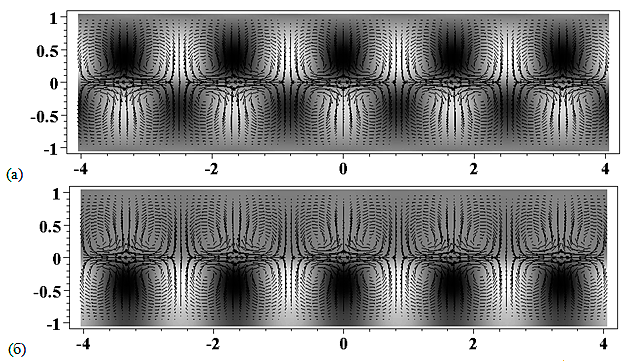
Рис. V.31. Структура критических возмущений температуры (а) и концентрации (б) в слоях при $\textit{h} = 0,5$. Критические параметры: $\textit{k} = 3.76$, $\Delta \textit{T} = -1,24 {}^{\rm o} С$
4. Рассмотрена задача о стационарном двумерном течении жидкости в вертикальном цилиндре в условиях радиационного нагрева применительно к естественным водоемам (оз. Байкал). Течение описывается уравнениями Обербека-Буссинеска при следующих дополнительных предположениях:
1) уравнение состояния жидкости принимается в виде $\rho = \rho {}_{0} (1 — \alpha (\theta — \theta {}_{0}) {}^{2})$. Такая немонотонная зависимость плотности от температуры описывает аномалию теплового расширения, свойственную воде при температурах, близких к $4{}^{\rm o} С$;
2) учтены объемные источники тепла. В уравнение энергии добавлена общая энергетическая функция теплового источника $F_{w} =\sigma \kappa R_{b} \exp (-\kappa z)$, описывающая проникновение солнечной радиации в жидкую среду. Учет влияния радиационного прогрева позволяет описать появление термоклина внутри водной толщи, что согласуется с известными результатами наблюдений.
Построено точное решение, содержащее независимый параметр $a_{1} $:
\[u=(u_{1} ,v_{1} ,w_{1} ),\, \, \, u_{1} =u(z)r,\, \, \, v_{1} =0,\, \, \, w_{1} =w(z),\, \, \, \, \, \, \theta =\theta (z),\, \, \, \, p(r,z)=q(z)+\frac{a_{1} }{2} r^{2}.~~~~~~~~~~(V.15)\]
Это решение является плоским аналогом решения Хименца уравнений Навье-Стокса. Оказалось, что если функция $\textit{u}$ известна, то остальные искомые функции находятся с помощью простых преобразований.
Для определения функции $u$ сформулирована двухточечная краевая задача
\[u_{zz} +2u_{z} \int _{0}^{z}u(z)dz -u_{}^{2} +a=0,\, \, \, \, \, \, 0 \lt z \lt 1,~~~~~~~~~~~(V.16)\]
\[u(0)=u(1)=0,\, \, \, \, \, \int _{0}^{1}u(z)dz =0,~~~~~~~~~~~~(V.17)\]
содержащая дополнительное интегральное условие и свободный параметр $\textit{а}$, задающий квадратичную зависимость давления от радиальной координаты $\textit{r}$. Краевая задача (V.16) — (V.17) для функции $u_{1}$ сводится к операторному уравнению $\textit{u = Au}$ с сильно нелинейным оператором $\textit{A}$. На основании теоремы Шаудера доказана разрешимость этого операторного уравнения. Численный анализ задачи обнаружил наличие трех неподвижных точек соответствующего отображения и отвечающих им значений параметра а: $a^{1} =-7.341\cdot 10^{-6} $, $a^{2} =9.12\cdot 10^{-7} $, $a^{3} =12.0168$. Первые два значения малы и позволяют интерпретировать построенное решение как приближенно описывающее течение в центральной части цилиндра большого, но конечного радиуса. Третье значение настолько велико, что не допускает разумной физической интерпретации, поскольку при таких значениях свободного параметра давление должно существенно изменяться в радиальном направлении. Разница между давлением на оси цилиндра p(0, z) и давлением p(10, z) (т.е. r = 10 м) составляет 0,13 бар, если же r = 1000, то разница уже порядка 1300 бар.
Поскольку решение является осесимметричным, то результаты расчетов на рис. V.32 — V.33 приведены для половины цилиндра $r\in (0,R).$
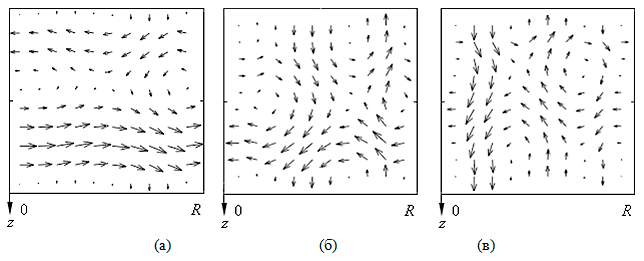
Рис. V.32. Поля скоростей: а — $a^{1}=-7,341\cdot 10^{-6}$; б — $a^{2}=9.12\cdot 10^{-7}$; в — $a^{3}=12,0168$
Следует отметить, что во всех случаях наблюдается формирование вихрей вблизи координаты инверсии температуры. Фактически это означает, что в области формирования термоклина имеет место интенсивный массоперенос.
В рамках линейной теории исследована устойчивость всех полученных классов течений. Выделена наиболее опасная плоская колебательная мода. В длинноволновой области неустойчивость связана с развитием тепловых волн. Определены критические числа Грасгофа, которые зависят от величины свободного параметра: $Gr{}_{1} = 1994.21$ при $a{}^{1}$, $Gr{}_{2} = 1764.7$ при $a{}^{2}$, $Gr{}_{3} = 24509.8$ при $a{}^{3}$. В коротковолновой области от колебательной моды ответвляется гидродинамическая мода. При положительных значениях независимого параметра обе ветви соединяются через петлю и имеют место оба механизма неустойчивости.
Поскольку наиболее опасная мода — тепловая, исследована эволюция колебательной моды в зависимости от числа Прандтля (рис. V.34). Оказалось, что при малых числах Прандтля колебательная мода разрушается и гидродинамический механизм неустойчивости становится основным дестабилизируюшим фактором.
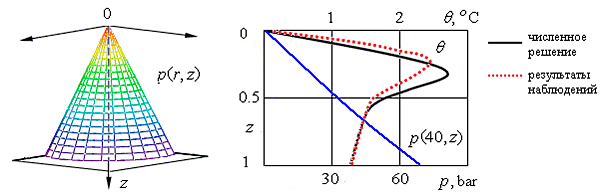
Рис. V.33. Характерные распределение давления p(r,z) в цилиндре и распределения давления и температуры по глубине
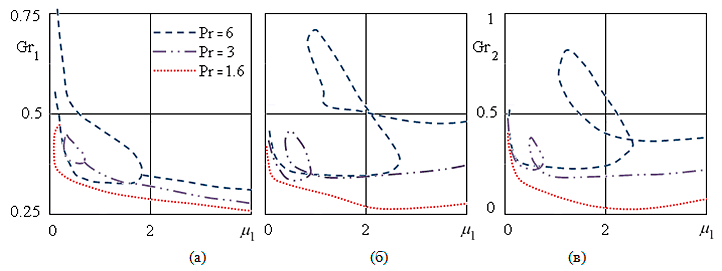
Рис. V.34. Нейтральные кривые. $Gr{}_{1} = Gr \cdot 10{}^{5}$, $Gr{}_{2} = Gr \cdot 10{}^{6}$: а — $a^{1}=-7,341\cdot 10^{-6}$; б — $a^{2}=9,12\cdot 10^{-7}$; в — $a^{3}=12,0168$
В случае монотонной потери устойчивости в системе могут развиться вторичные движения. Особенности этих движений могут быть изучены только путем анализа полных нелинейных уравнений для возмущений $\textit{U}$, $\textit{V}$, $\textit{W}$, $\textit{P}$, $\textit{T}$ основного решения (V.14). Учитывая результат линейного анализа, будем рассматривать только осесимметричные возмущения. Получим следующую задачу в безразмерных переменных для возмущений:
\[U_{t} +ruU_{r} +UU_{r} +uU+ru_{z} W+wU{}_{z} +WU_{z} -\frac{V^{2} }{r} +P_{r} =U_{rr} +\frac{U_{r} }{r} +U_{zz} -\frac{U_{r} }{r^{2} } -\frac{2V}{r^{2} } ,\]
\[V_{t} +ruV_{r} +UV_{r} +wV_{z} +WV_{z} +uV+\frac{UV}{r} =V_{rr} +\frac{V_{r} }{r} +V_{zz} -\frac{V}{r^{2} },~~~~~~~~~~(V.17)\]
\[W_{t} +ruW_{r} +UW_{r} +Ww_{z} +wW_{z} +WW_{z} +P_{z} =W_{rr} +\frac{W_{r} }{r} +W_{zz} -{\rm Gr}\left({\rm T}^{{\rm 2}} {\rm +2T(}\theta -{\rm 1)}\right),\]
\[U_{r} +\frac{U}{r} +W_{z} =0,\]
\[T_{t} +ruT_{r} +UT_{r} +W\theta _{z} +wT_{z} +WT_{z} =\frac{1}{{\rm Pr}} \left(T_{rr} +\frac{T_{r} }{r} +T_{zz} \right),\]
\[z=0:\, \, \, \, \, \, U=V=W=T_{z}=0,\] \[z=1:\, \, \, \, \, \, U=V=W=T=0.~~~~~~~~~~(V.18)\]
Определены закритичные режимы течения в классах функций периодическим по радиальной координате $\textit{r}$ с периодом $2 \pi /\mu 1$. Для решения задачи (V.17) — (V.18) использовался метод малого параметра, согласно которому решение ищется в виде
\[(U,P,T)=\sum _{n=1}^{\infty }\varepsilon ^{n} (U^{(n)} ,P^{(n)} ,T^{(n)} ),\, \, \, \, \, \, {\rm Gr}\, {\rm =}\sum _{n=1}^{\infty }\varepsilon ^{n} {\rm Gr}^{(n)} ,\, \, \, \, \, \, \varepsilon =\varepsilon ({\rm Gr})-{\rm Gr}_{{\rm кр}} .\]
Выполненные вычисления показывают, что во всей области существования плоской моды вторичные режимы существуют для всех значений параметра $\textit{a}$. Течение является осесимметричным и имеет сложную многовихревую структуру (рис. V.35). Формирование некоторых вихрей происходит в области термоклина (выделена цветом) или вблизи нее.
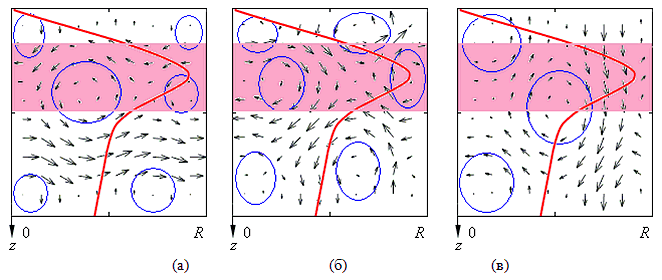
Рис. V.35. Поля скорости вторичного течения: а — $a^{1} =-7.341\cdot 10^{-6}$; б — $a^{2} =9.12\cdot 10^{-7}$; в — $a^{3} =12.0168$
При колебательной потере устойчивости могут быть вычислены мгновенные поля скоростей как решение задачи (V.16) — (V.17) для разложений первого порядка. Использовался метод конечных разностей. Одновременно применялись две схемы: первая — явная схема второго порядка, вторая — продольно-поперечная схема. Шаги определялись из условий устойчивости. При закритичных значениях числа Грасгофа в области колебательной неустойчивости оказалось, что два вихря формируются вблизи координаты инверсии, которая совершает периодические колебания в выделенной области (рис. V.36), причем имеется некоторое время задержки, с которым колебания вихрей отвечают на колебания теплового поля. (В. Б. Бекежанова)
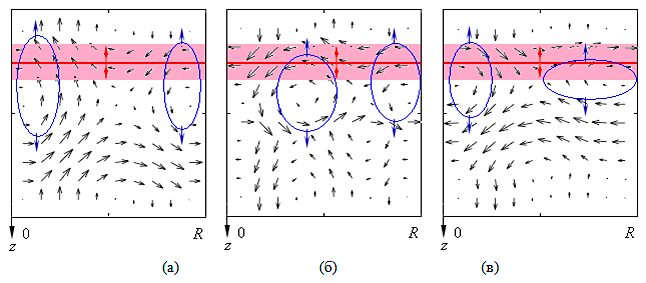
Рис. V.36. Мгновенные поля скорости возмущенного течения при колебательной неустойчивости
5. Рассмотрена задача о конвективном однонаправленном течении двухслойной жидкости на наклонной плоскости (рис. V.37). В предположении о недеформируемости общей поверхности раздела и свободной поверхности изучено обобщение решения типа Остроумова — Бириха. Указанное решение описывает совместное течение двух вязких теплопроводных жидкостей в системе с заданным продольным градиентом температуры на нижней твердой стенке.
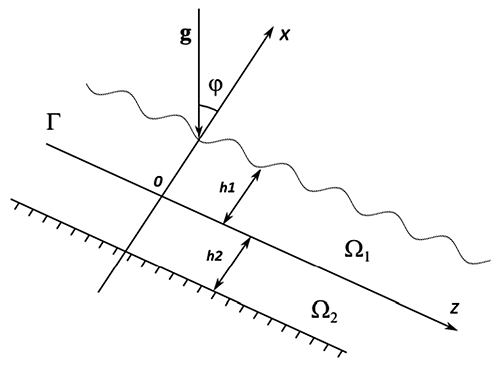
Рис. V.37. Схема течения
В силу дополнительного классифицирующего условия задача допускает несколько классов течений: 1) в отсутствие продольного градиента температур, 2) в условиях микрогравитации, 3) в горизонтальном слое, 4) при ограничении на свойства жидких сред $\rho{}_{1} \beta{}_{1} = \rho{}_{2} \beta{}_{2}$. В последнем условии $\textit{$\rho$}$ — плотность соответствующей среды, $\textit{$\beta $}$ — коэффициент теплового расширения.
Для подробного анализа полученного множества решений каждый класс должен быть исследован в отдельности. В случае, когда g = 0, рассматривается течение в условиях невесомости, при этом система произвольно ориентирована в пространстве и решение не зависит от угла наклона $\varphi $. Получен точный вид для функций давления, скорости и температур в каждом из слоев:
\[p_{i} (z)=\rho _{i} a_{i} z+b_{i},\] \[u_{i} (x)=\frac{a_{i} }{2\nu _{i} } x^{2} +C_{3}^{i} x+C_{4}^{i},\] \[T_{i} (x,z)=(M_{i} x+N_{i} )z+F_{i} (x),\]
где постоянные $C_{3}^{i}, \, \, C_{4}^{i}, \, \, M{}_{i}, \, \, N{}_{i}, \, \, i,j = 1,2$ определяются из граничных условий как решение системы линейных алгебраических уравнений. Функции $\textit{F${}_{i}$}$ определяются из уравнения $\chi _{i} F_{i} ^{{'} {'} } (x)=(M_{i} x+N_{i} )u_{i} (x)$, т.е. $\textit{F${}_{i}$}$ — полиномы пятого порядка по $\textit{x}$. Поскольку рассматривается течение со свободной границей и задано давление газа $\textit{p${}_{g}$}$ вне жидкости, то из граничных условий однозначно определяются $\textit{a${}_{i}$}$ и $\textit{b${}_{i}$}$.
Для системы глицерин-керосин построены характерные профили скоростей и температур при различных значениях продольного градиента температуры A. Оказалось, что термокапиллярный эффект существенным образом влияет на формирование поля скорости в системе. Наиболее интенсивный характер течение имеет в верхнем слое (рис. V.38). С ростом толщины слоев влияние величины продольного градиента температуры ослабевает (В. Б. Бекежанова).
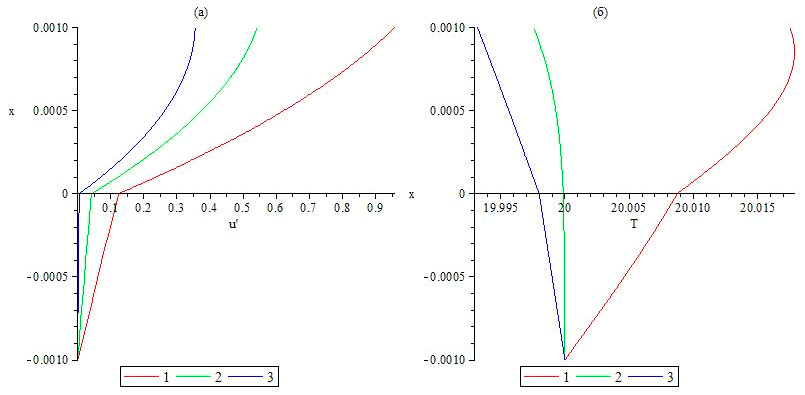
Рис. V.38. Профили скоростей (а), температур (б) для $h{}_{1} = 10{}^{-3}$, $h{}_{2} = 10{}^{-3}$, $u' = u \cdot 10{}^{3}$; 1 — $A =3{}^{\rm o} C/м$, 2 — $A = 1{}^{\rm o} C/м$, 3 — $A = 0.1{}^{\rm o} C/м$
Основные публикации:
- Андреев В. К., Бекежанова В. Б.
Устойчивость неизотермических жидкостей (обзор) // ПМТФ, 2013. — Т. 54. — № 2. — P. 3-20. - Andreev V. K., Ryzhkov I. I.
On thermocapillary instability of a liquid column with a co-axial gas flow // J. of Siberian Federal University. Mathematics and Physics. — 2013. — Vol. 6. — № 1. — P. 3-17. - Lemeshkova E. N.
Сombined Motion of Three Viscous Heat-conducting Liquids in a Flat Layer // J. of Siberian Federal University. Mathematics and Physics, 2013. — Т. 6. — № 2. — P. 211–219 .
(Отдел дифференциальных уравнений механики)
| К началу | |
Проект № 73. «Современные технологии формирования информационной инфраструктуры для поддержки междисциплинарных исследований, в том числе для мониторинга природных и социальных процессов территорий Сибири и Дальнего Востока»
Руководитель проекта: академик РАН Ю. И. Шокин
Ответственный исполнитель от ИВМ СО РАН: к.ф.-м.н. О. Э. Якубайлик
Исполнители: А. А. Кадочников, А. Г. Матвеев, В. В. Ничепорчук
1. Выполнялись работы по анализу механизмов оптимизации доступа к географическим пространственным данным в распределенной вычислительной среде, формированию эффективной информационной инфраструктуры для доступа к данным и их обработки, прежде всего — с помощью специализированных геопространственных веб-сервисов и графических пользовательских интерфейсов.
Были рассмотрены следующие типы сетевых сервисов для работы с географическими пространственными данными:
- поисковые сервисы, позволяющие искать наборы пространственных данных и геосервисы на основе соответствующих метаданных и отображать содержание метаданных;
- сервисы визуализации, предоставляющие, как минимум, возможности просмотра данных, навигации по изображениям, их скроллинга, масштабирования и графического оверлея данных, а также отображения легенд карт и соответствующей информации, содержащейся в метаданных;
- сервисы для скачивания информации, позволяющие копировать наборы пространственных данных или их фрагменты и, по возможности, обеспечивающие прямой доступ к данным;
- сервисы преобразования данных, дающие возможность трансформировать наборы пространственных данных с целью обеспечения их интероперабельности;
- сервисы для вызова других (удаленных) сервисов.
Перечисленные сервисы должны формировать основу программно-технологических решений для доступа к данным, имеющим географическую привязку — геопорталам, серверам пространственных метаданных. Их эффективная программная реализация — актуальная задача сегодняшнего дня.
Были также выполнены работы, связанные с инфраструктурным обеспечением проекта — по запуску в эксплуатацию нового серверного оборудования, размещенного в новом, специально оборудованном помещении серверной комнаты в здании ИВМ СО РАН. Была смонтирована и установлена стойка с серверным оборудованием, включающая несколько серверов, сетевое хранилище, сетевое оборудование и источники бесперебойного питания. Для непрерывной и стабильной работы были развернуты средства мониторинга работы серверных систем, включающие анализ нагрузки на процессор, оперативную память, жесткие диски, сетевую нагрузку, а также количество работающих и ожидающих процессов, подключенных пользователей, и т.п. Настроено корректное отключение серверного оборудования в зависимости от сигналов источников бесперебойного питания с целью оградить серверное оборудование от сбоев питания и неблагоприятных условий окружающей среды благодаря поддержанию постоянных климатических условий внутри серверного помещения (Рис. V.39).

Рис. V.39. Новая стойка с серверным оборудованием в ИВМ СО РАН
На базе сервера HP ProLiant DL160 развернут автономный гипервизор — операционная система, которая устанавливается на сервер и позволяет создавать и запускать виртуальные машины. Роль автономного гипервизора выполняет серверное программное обеспечение VMware ESXi 5.1, которое представляет собой операционную систему (без консоли управления), созданную для запуска и управления виртуальными машинами.
Для управления виртуальными машинами на автономном гипервизоре применяется программное обеспечение VMware vSphere Client. Для управления виртуальными серверами на уровне командных сценариев (например, выключение по сигналу от источника бесперебойного питания, создание резервных копий дисков виртуальных машин, или создания рабочее копии самого гипервизора) установлено и настроено программное обеспечение VMware vSphere Management Assistant (vMA), которое позволяет централизованно управлять хост-серверами VMware ESXi за счет автоматизации операций системных администраторов.
В результате администратору становится проще контролировать конфигурацию серверов ESXi и исполнять рутинные операции для большого количества объектов. Можно сказать, что vSphere Management Assistant представляет собой «вынесенную» за пределы серверов VMware ESXi сервисную консоль (консольную ОС), которая для виртуальной инфраструктуры присутствует в единственном экземпляре, но централизованно исполняет сценарии на хостах, используя различные интерфейсы VMware ESXi.
Для размещения виртуальных машин к серверу с ESXi подключено сетевое файловое хранилище с применением iSCSI по 2х гигабитному каналу. iSCSI — это протокол, который базируется на TCP/IP и разработан для установления взаимодействия и управления системами хранения данных, серверами и клиентами. Физически протокол инкапсулирует SCSI блоки в пакеты Ethernet.
На базе гипервизора VMWare ESXi 5.1 создано несколько виртуальных серверов. На виртуальных серверах установлены операционные системы FreeBSD 9.1 и OpenSUSE 12 (x86_64) с графической средой Gnome для тестирования LDAP.
Сформирован отдельный физический сервер для создания карт на основе растровых фрагментов («тайловых подложек»). На этот сервер перемещены основные «тайловые карты» Красноярского края и в ближайшее время на этом сервере будут динамически создаваться «тайловые карты» для разных карт геопортала СО РАН.
Таким образом, выполненные работы по совершенствованию существующей информационной инфраструктуры позволят значительно повысить эффективность доступа к геопространственным данным ИВМ СО РАН, ускорить процесс загрузки тематичесих карт на стороне клиента.
2. На основе проведенного анализа для геопортала выбрана система классификации пространственных данных. Рассматривались различные иерархические и неиерархические системы классификации; таксономия, фолксономия и фасеты. Оценивались их положительные и негативные особенности, достоинства и недостатки. Задача рассматривалась прежде всего с точки зрения достижения максимальной простоты использования при соблюдении основных функциональных требований.
Поиск пространственных данных должен осуществляться с использованием модели организации данных, удобной в управлении и формировании запросов, наглядной и визуально легко воспринимаемой любым пользователем. Такая модель должна сочетать в себе наглядность иерархической модели и гибкость неиерархических моделей. Оптимальным в вопросе выбора системы классификации, становится фасетная классификация, в основе которой лежит возможность создания иерархических фасетов. При этом основные преимущества таксономии (наглядность, обозримость, привычность для пользователя и т.д.) можно реализовать на уровне пользовательского интерфейса.
Принципы и система классификации пространственных данных являются важнейшими вопросами при формировании инфраструктуры пространственных данных (ИПД). В частности, рассматривая один из элементов ядра метаданных для описания пространственных данных — раздел «Предметная область» — можно обнаружить, что в справочнике предметных областей международного стандарта ISO 19115:2003 и его национальном профиле ГОСТ Р 52573 2006 «Географическая информация. Метаданные» (которые стандартизируют правила описания пространственных данных) насчитывается 19 пунктов. Однако есть альтернативные рубрикаторы — системы GEOSS (Общемировой системы систем Исследования Земли из космоса — Global Earth Observation System of Systems), европейского проекта по созданию инфраструктуры пространственной информации ЕС — INSPIRE (Infrastructure for Spatial Information in Europe), национальных мультидисциплинарных атласов различных стран, и проч. Во всех этих системах используются собственные справочники.
Наиболее целесообразным представляется проектирование и разработка таких информационных систем, в которых обеспечена возможность работы с несколькими системами классификации, и которые предоставляют пользователю возможность выбора такой системы. Именно такой системой является геопортал ИВМ СО РАН.
Рассмотренные технологии легли в основу выполненной разработки — веб-интерфейса клиентского приложения системы управления пространственными метаданными «Каталог метаданных» геопортала ИВМ СО РАН. Задачей этого веб-приложения является навигация по каталогу пространственных метаданных, с поиском и фильтрацией данных по различным критериям. По принципам организации и внешнему виду выполненная разработка похожа на многие популярные системы каталогизации в Интернет — Яндекс.Каталог, Товары@Mail.Ru, Yahoo! Directory, и проч. (Рис V.40.).
Отметим некоторые ее отличительные характеристики.
- Система основана на принципах множественной (фасетной) классификации, благодаря которой ресурсы каталога группируются по разным логическим иерархиям, с динамическим подсчетом различных характеристик сгруппированных ресурсов по выбранным разделам и подразделам.
- Развитый пользовательский интерфейс для представления метаданных — динамически формируемые сведения о выбранном разделе каталога (количество ресурсов, категории фильтрации данных, режимы отображения информации из вложенных разделов, и т.д.) и конкретном ресурсе (информация структурируется по подразделам через систему информационных страниц, размещаемых на разных раскрывающихся вкладках), набор ссылок для прямого доступа к данным (WMS -сервисы, zip-файлы с архивами, и т.п.).
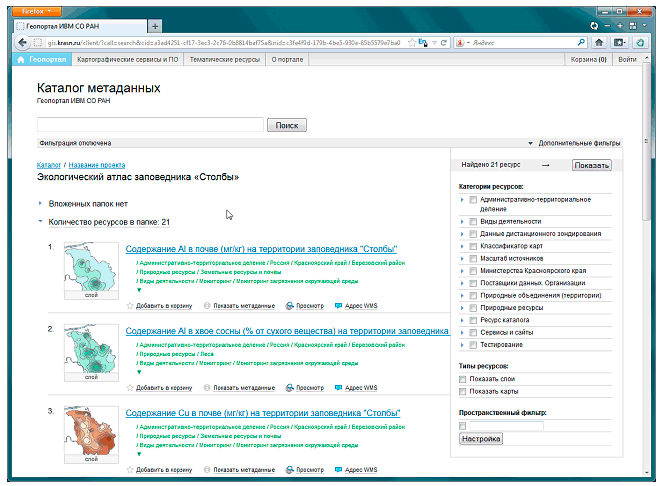
Рис. V.40. Интерфейс веб-приложения «Каталог метаданных» геопортала ИВМ СО РАН - Средства полнотекстового поиска и фильтрации ресурсов по метаданным (название, описание, авторы, и проч.), а также — по пространственным локализациям данных (выделением области поиска на интерактивной карте).
- Просмотр картографических ресурсов каталога двумя способами — либо при помощи встроенной системы картографической веб-визуализации, либо с помощью сторонних приложений, через WMS-протокол.
- Средства персонализации интерфейса пользователя — возможность выбора и переноса ресурсов каталога метаданных во временное хранилище («Корзина») или сохранения в постоянное хранилище («Мои документы»).
Основные публикации:
- Матвеев А. Г. Система управления контентом геоинформационного веб-портала «Геофреймворк» / А. Г. Матвеев, О. Э. Якубайлик
// Современные проблемы науки и образования. — 2013. — № 6; URL: www.science-education.ru/113–109 97 (дата обращения: 05.12.2013). - Программно-технологическое обеспечение геопортала ИВМ СО РАН / Якубайлик О. Э., Кадочников А. А., Матвеев А. Г., Пятаев А. С., Токарев А. В.
// Электронные библиотеки, 2013. — Т. 16. — Вып. 5; URL: http://www.elbib.ru/index.phtml?page=elbib/rus/journal/2013/part5/YKMPT.
(Отдел вычислительной физики)
| К началу | |
Проект № 74. «Разработка принципов и информационно-вычислительных технологий обработки и интерпретации мультиспектральных спутниковых изображений высокого и сверхвысокого пространственного разрешения (для наук о Земле, экологии и природопользования)»
Руководитель проекта: д.ф.-м.н. О. И. Потатуркин
Ответственный исполнитель от ИВМ СО РАН: к.ф.-м.н. О. Э. Якубайлик
Исполнители: А. А. Кадочников, А. Г. Матвеев, В. В. Ничепорчук
1. Анализ, проектирование и разработка программно-алгоритмического обеспечения для обработки спутниковых изображений на основе системы прикладных геопространственных веб-сервисов.
Рассматривались различные варианты структуры и архитектуры необходимого программного обеспечения, механизмы обработки данных и организации вычислений. Предполагается, что создаваемые программные средства в значительной степени ориентированы на существующую программно-технологическую основу геопортала ИВМ СО РАН — используются его возможности по регистрации и хранению, описанию и визуализации — как исходных спутниковых данных, так и результатов их анализа.
Основные направления исследований и результаты связаны с решением следующих задач:
- разработка проектного решения, обеспечивающего возможность внедрение методов обработки пространственных данных в существующий геопортал ИВМ СО РАН, в т.ч. с возможностью построения независимых веб-приложений, основанных на сервисах геопортала;
- разработка обобщенного интерфейса методов обработки пространственных данных, обеспечивающего простое добавление новых методов обработки без нарушения работоспособности уже существующих;
- обеспечение поддержки стандарта WPS для обеспечения возможности использования уже созданных методов обработки пространственных данных из сторонних прикладных программ, поддерживающих этот протокол;
- обеспечение максимальной автономности создаваемого программного обеспечения от существующего функционала геопортала ИВМ СО РАН.
Разработка выполняется с использованием следующие инструментов: языки программирования C++ и PHP; библиотеки boost, GDAL, Xalan, сервер Apache. Алгоритм работы данной системы выглядит следующим образом:
1) пользователь выбирает исходные данные в каталоге геопортала;
2) выбирает метод или набор (пакет) методов обработки;
3) заполняет параметры вызова и конфигурацию;
4) запускает систему вычислений.
При запуске расчета в каталоге геопортала создаётся выходной объект, в котором хранится информация о процессе вычисления. После завершения этого процесса результаты обработки сохраняются на сервере, при этом метаданные формируются автоматически. Пользователю доступны все возможности визуализации результата обработки, имеющиеся на геопортале.
UML-диаграмма ключевых классов прототипа создаваемого программного обеспечения представлена на рис. V.40.
Основным базовым классом для всех методов обработки данных является класс WPAbstractService (интерфейсный класс «Шаблонный метод»). Этот класс обязывает наследников реализовывать функции GetSignature(), GetResult(). Первая функция возвращает сигнатуру WPS метода в формате XML, вторая возвращает результат работы данного метода в том же формате. Обе эти функции могут быть использованы для создания интерфейса пользователя будущего метода. Для полной инкапсуляции класс также содержит функции GetFormXSLT(), GetResultXSLT(), которые возвращают правила преобразования данных XML в HTML страницы. Данные функции не используются, если необходимо генерировать страницы самостоятельно, например, с помощью технологий Javascript/AJAX .
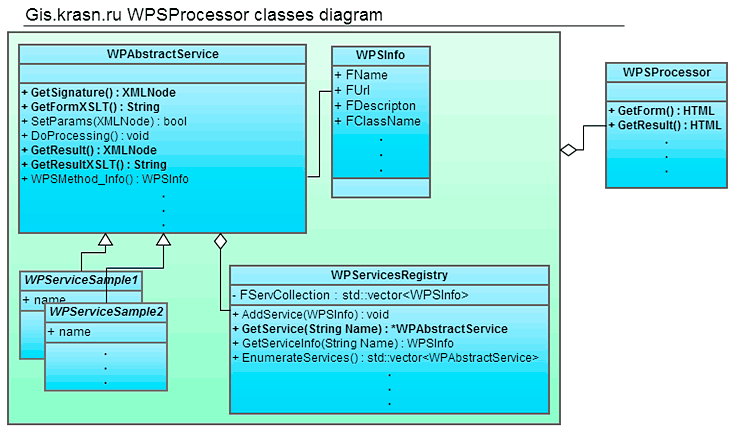
Рис. V.41. Схема программной реализации (основные классы)
Ещё один ключевой класс — WPServiceRegistry, который соответствует шаблону «Абстрактная фабрика». Данный класс создан как реестр существующих WPS, он содержит коллекцию структур, которые описывают все существующие методы. С помощью этого класса сокращается код, необходимый для вызова или добавления нового метода. Основная функция GetService (String Name) возвращает указатель на созданный объект. Кроме того, пользователь ограждается от упоминания конкретного названия метода в коде. Мы также избавляемся от проблем, связанных с выделением памяти и устойчивости к исключениям (Exception safe), поскольку объекты класса WPserviceRegistry агрегируют в себе объекты класса WPAbstractService и полностью управляют созданием и уничтожением с помощью техники «Получение ресурса есть инициализация (RAII)». Последний факт важен для стабильности системы, потому что каждый метод может при создании инициализировать некоторые системные компоненты, которые обязательно должны быть корректно отключены.
В контексте предложенной архитектуры ПО рассмотрим схему взаимодействия геопортала и экземпляра WPS (одного из зарегистрированных методов обработки данных). Объект WPAbstractService в контексте геопортала является просто черным ящиком; единственная доступная информация — это название метода. Для его вызова необходимо сделать запрос на URL с названием метода, все остальное сделает сам метод — покажет форму вызова, примет данные, обработает, покажет результат и переадресует на нужную страницу (см. рис. V.42).
В настоящее время доступ к программе на C++ происходит по технологии CGI. Еще одна особенность реализации — в механизме доступа к сервисам обработки данных через API-ключ аналогично другим существующим сервисам геопортала. Это позволяет использовать весь функционал системы, в том числе, — сквозную систему аутентификации пользователей.
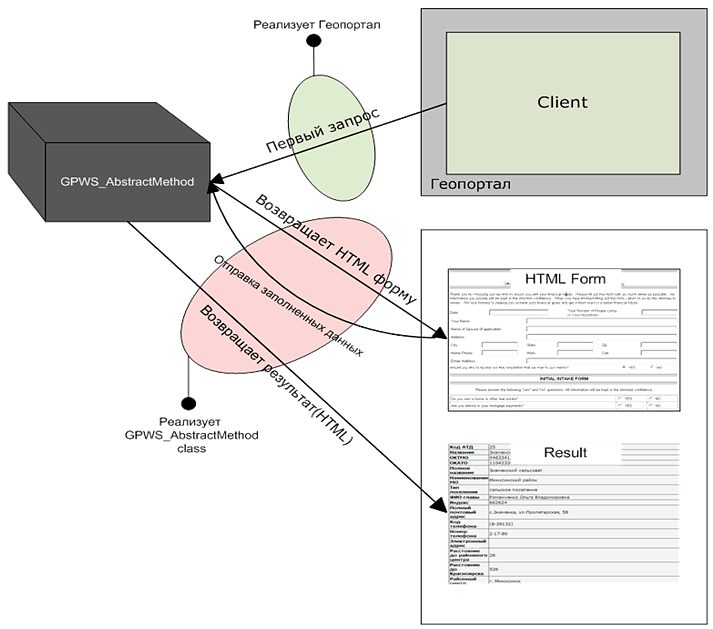
Рис. V.42. Схема взаимодействия геопортала и экземпляра класса GPWSAbstractMethod
2. Создание специализированной системы для разработки геоинформационных веб-приложений — инструментальных программных средств для интеграции и настройки веб-компонентов.
Система состоит из клиентской и серверной частей, реализуя тем самым технологию «клиент — сервер». Применение в основе серверной части приложения шаблона проектирования MVC (модель — представление — контроллер) предоставляет широкие возможности для решения поставленных задач. Использование данной архитектуры предполагает разделение данных приложения, пользовательского интерфейса и управляющей логики на три отдельных компонента (Рис. V.43). Модификация каждого компонента может осуществляться независимо. Помимо стандартных элементов MVC ключевыми блоками рассматриваемой системы также являются шаблоны представления страниц и AJAX-обработчики.
Основные компоненты архитектуры системы.
Модель (Model)
Каждый раздел Интернет-сайта, построенного на основе описываемой платформы, связан с одной (или несколькими, иерархично расположенными) моделями, основной задачей которых является реализация бизнес-логики приложения. Модели в зависимости от параметров запроса (которые предоставляются контроллером системы) осуществляют следующие действия:
- получение или изменение данных предметной области;
- определение представления и шаблона представления страницы, соответствующего параметрам запроса;
- подготовка выходного набора данных для использования в представлении.
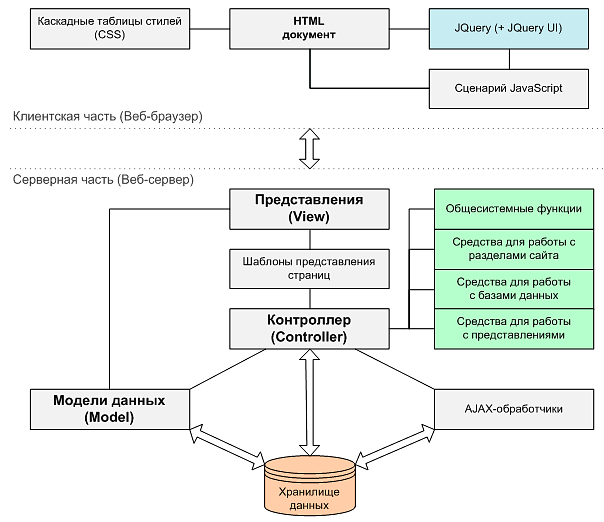
Рис. V.43. Архитектура системы разработки геоинформационных веб-приложений
Представление (View)
Отвечает за отображение данных предметной области (предоставляемые моделью). Один раздел сайта может иметь несколько различных отображений, изменяемых в зависимости от контекста. Например, представление list содержит список записей, содержащихся в таблице, а представление edit содержит форму для создания и редактирования этих записей. Разделение логики предметной области и отображения данных является безусловным преимуществом шаблона MVC и практически необходимым условием при реализации многофункциональных веб-приложений.
Контроллер (Controller)
Является связующим звеном между прочими компонентами системы. Большинство HTTP-запросов перенаправляется для обработки контроллеру. Основными задачами контроллера являются:
- подключение настроек, внутренних и внешних библиотек;
- приём и анализ HTTP-запросов;
- выбор на основе параметров запроса необходимой модели и передача ей управления;
- подключение необходимого шаблона представления страницы;
- формирование заголовков ответа HTTP и вывод данных.
Шаблон представления страницы
Формально является составной частью представления (View), но фактически является самостоятельным элементом системы. Средний по функциональности веб-сайт имеет 1-3 шаблона страницы, каждый из которых представляет собой подключаемый к контроллеру PHP-сценарий, содержащий общие для используемых представлений элементы (X)HTML-кода страницы — заголовочная секция, ссылки на необходимые файлы каскадных таблиц стилей и сценариев JavaScript, метаописания веб-страниц и общие элементы DOM. Выбираемый моделью файл представления затем встраивается в указанный шаблон, и в результате генерируется полный (X)HTML-код веб-страницы.
AJAX-обработчик
Представляет собой модель, предназначенную для работы с асинхронными запросами.
Рассматриваемая система использует развитый механизм создания веб-страниц на основе шаблонов; технологии XHTML, CSS для формирования компактного эффективного программного кода, на основе объектной модели документа. Она является важных звеном в программно-алгоритмическом обеспечении для обработки спутниковых изображений на основе системы прикладных геопространственных веб-сервисов.
Основные публикации:
- Якубайлик О. Э.
Технологии для прикладных геоинформационных веб-систем // Материалы VI Междунар. науч. конф. «Актуальные вопросы современной науки». — Cт.-Петербург: «Айсинг», 2013. — С. 29-39. - Якубайлик О. Э.
Формирование программно-технологического обеспечения системы мониторинга состояния природной среды и ресурсов // Сб. докл. XIII Междунар. науч. конф. «Актуальные вопросы современной техники и технологии». — Липецк: «Гравис», 2013. — С. 51-55. - Якубайлик О. Э.
Исследование возможностей современного программно-технологического обеспечения для построения геопорталов // Сб. ст. по материалам XII Междунар. науч.-практ. конф. «Естественные и математические науки в современном мире». — Новосибирск: СибАК, 2013. — С. 77-82.
(Отдел вычислительной физики)
| К началу | |
Проект № 4. «Концепция устойчивого развития и природно-техногенной безопасности территорий Беларуси и Сибири, построенная на основе учета рисков и с применением геоинформационных технологий»
Руководитель проекта: д.ф.-м.н. Н. Я. Шапарев
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н. Н. Я. Шапарев
Исполнители: А. В. Андрианова, В. В. Ничепорчук (ИВМ СО РАН), В. В. Москвичев, А. М. Лепихин, Н. А. Чернякова (СКТБ «Наука»), Ю. И. Шокин (ИВТ СО РАН)
На данном этапе рассматривалась река Енисей в показателях устойчивого природопользования. Для этой цели была сформирована система критериев для наблюдения и контроля за состоянием водной среды с использованием не только классических инструментальных (физико- химических) методов, но и биологических, учитывающих ответную реакцию биоты на изменение качества среды обитания. Сформированная система включает 4 показателя: (гидрографический, гидробиологический, социально-экономический, состояние сточных и качество поверхностных вод). Содержательное наполнение показателей выполнено на основе статистических данных, аналитических оценок и результатов, полученных в экспедиционных исследованиях. Разработанная комплексная система показателей устойчивого природопользования позволяет определить степень устойчивости водного объекта.
Полученные результаты позволяют сделать следующие выводы: плотность гидрологических сетей в бассейне является недостаточной; доля площади вырубаемых лесов в бассейне составляет 0.025 %; доля распаханности территории бассейна составляет 1.16 %; забор свежей воды около 1.3 %. Таким образом, входное воздействие в бассейне реки является незначительным, но недостаточно контролируемым.
Социально-экономическое состояние водопользования таково: техническое состояние системы водоснабжения имеет степень износа более 80 %, поэтому возникают большие потери воды при транспортировке (около 4 %) и ухудшается качество доставляемой питьевой воды. Бытовое потребление воды на душу населения составляет около 240 литров в сутки, что в 1.5 раза ниже, чем в среднем по России, но в 2 раза выше европейских показателей. Около 30 % населения региона потребляют воду, не отвечающую гигиеническим нормативам. Доля повторно-последовательного и оборотного использования воды низка, а величина водопользования на единицу ВВП в 1.4 раза выше, чем в России и в несколько раз превосходит этот показатель в Германии, Англии, Японии. Причина этого кроется в неэффективности водопользования и в наличии промышленности, которая связана с энергетикой и добычей природных ресурсов. Однако этот показатель в последние годы улучшается.
Забор свежей воды в связи с падением экономики значительно уменьшился. Уменьшение водозабора привело к уменьшению сброса сточных вод, которые разделяются по категориям: нормативно-чистые, загрязнённые недостаточно-очищенные, загрязнённые (без очистки), нормативно-очищенные. Сброс сточных вод в поверхностные водные объекты обусловлен: жилищно-коммунальным хозяйством — 69.8 %, транспортным и сельским хозяйством — 0.6 %, промышленностью — 29.5 % (электроэнергетика — 34.5 %, химическая и нефтехимическая — 10.1 %, цветная — 7.6 %, лесопереработка — 27 %, угольная — 17.1 %, прочие — 3.7 %). Объёмы загрязнённых вод, сбрасываемых без очистки, на 83 % обязаны промышленности, а на 11.3 % связаны с предприятиями жилищно-коммунального хозяйства. Общий вес загрязняющих веществ, поступающих со сточными водами в водные объекты, составляет около 300 000 тонн в год и в последние годы уменьшается. Уменьшение объёмов сброса сточных вод и загрязняющих веществ в водные объекты не привело к улучшению качества поверхностных вод. Красноярский край лидирует в Сибирском регионе по объёму сброса сточных вод. Уровень загрязнения воды р. Енисей, согласно российскому показателю УКИЗВ, оценивается как «загрязненная» (3 класс, разряд «а») и «грязная» (4 класс, разряд «а») (рис. V.44). Химические и биологические методы оценки качества воды в Енисее в основе своей показали сходные результаты.
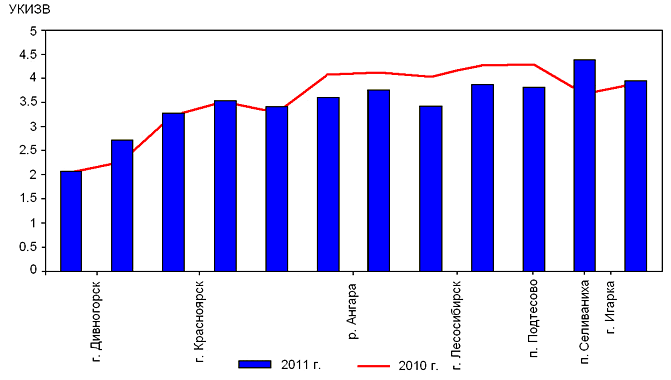
Рис. V.44. Динамика изменения величины УКИВЗ р. Енисей на участке от плотины Красноярской ГЭС до г. Игарка
Русловое зарегулирование Енисея привело к изменению термического режима реки, и как следствие — к нарушению устойчивости экосистемы. Произошла структурная перестройка биологических сообществ, резко сократилась численность многих ценных видов рыб. Экологическая ситуация в Енисее также усугубляется загрязнением сточными водами. Увеличение антропогенной нагрузки на экосистему Енисея привело к обогащению водной толщи биогенными элементами и органическими веществами, что стимулировало развитие фитопланктона, перифитона, зообентоса и обусловило повышение трофности водотока.
Все субъекты, входящие в Сибирский федеральный округ, отличаются следующими особенностями социально-экономического развития:
- низкой плотностью населения и коммуникаций, сосредоточением основной инфраструктуры в округе к югу от Транссибирской магистрали;
- ресурсоориентированной экономикой с приоритетом ресурсодобывающих и ресурсоперерабатывающих (в меньшей степени) отраслей экономики;
- неудовлетворительной экологической обстановкой в крупных городах, где проживает до 70 % населения;
- изменением климата и водного режима крупных рек, вызванного строительством гидроэлектростанций;
- реализацией крупных инвестиционных проектов в области промышленности, энергетики и транспорта, воздействующих на окружающую среду;
- слабым развитием сельского хозяйства, обусловленным климатическими и экономическими факторами.
По основным социально-экономическим и рискообразующим показателям регионы Сибири, особенно Красноярский край, можно рассматривать как модель России. Для этих территорий характерна проблема перераспределения ВВП, особенно при реализации инвестиционных проектов, когда одна группа получает значительную прибыль за счёт ухудшения условий жизни другой группы населения.
Для анализа и управления территориальными рисками необходимо использовать количественные оценки рисков ЧС. Один из простых вариантов — оценка риска по количеству зарегистрированных ЧС, чрезвычайных происшествий и других неблагоприятных событий. При этом подходе показатели опасности территорий оцениваются по статистике ЧС, чрезвычайных происшествий, пожаров и других событий с применением технологии оперативного анализа многомерных данных (OLAP) и динамического картографирования результатов анализа. На основе баз данных мониторинга опасностей, сводных докладов органов управления МЧС России, Ростехнадзора и других ведомств с помощью инструментария выполнен анализ данных отдельных показателей состояния территориальной безопасности субъектов СФО (табл. V.5).
На основании анализа рисков получены выводы, что территории, где ведётся активная хозяйственная деятельность, обладают повышенным риском ЧС и более напряженной экологической обстановкой. В то же время более высокий ВВП позволяет проводить мероприятия по повышению защищенности и снижению уязвимости объектов и инфраструктуры. Кроме городов Сибири, являющихся индустриальными центрами, «точками развития» можно считать Курагинский, Северо-Енисейский, Туруханский муниципальные районы Красноярского края, территорию Нижнего Приангарья, севера Томской области и другие, где реализуются инвестиционные проекты, связанные с использованием природных ресурсов. По прогнозам специалистов такая тенденция развития Сибирского федерального округа сохранится в течение ближайших 30-50 лет. Однако для территорий Сибири на путь устойчивого развития необходимо направление финансовых средств в наукоемкие отрасли экономики, технологии глубокой переработки сырья, сельское хозяйство, мероприятия по улучшению экологической обстановки. Это достижимо при пересмотре законодательства (в том числе и федерального), повышения эффективности работы органов управления территориями по предупреждению и адекватному реагированию на проявление опасностей.
| Субъект Сибирского федерального округа | Население, тыс. чел | Погибло*, чел. | Суммарный риск | ||
|---|---|---|---|---|---|
| в ЧС 20 | в пожарах 19 | в ДТП 20 | |||
| Республика Алтай | 202.9 | 68 | 51 | 71 | 71 |
| Республика Бурятия | 981 | 234 | 210 | 273 | 273 |
| Республика Тыва | 305.5 | 155 | 25 | 129 | 129 |
| Республика Хакасия | 546.1 | 95 | 96 | 169 | 169 |
| Алтайский край | 2607.2 | 652 | 529 | 427 | 427 |
| Забайкальский край | 1156.2 | 339 | 247 | 334 | 334 |
| Красноярский край | 2966.2 | 761 | 664 | 580 | 580 |
| Иркутская область | 2581.6 | 848 | 623 | 504 | 504 |
| Кемеровская область | 2900.2 | 649 | 596 | 464 | 464 |
| Новосибирская область | 2692.2 | 550 | 499 | 416 | 416 |
| Омская область | 2079.2 | 471 | 444 | 224 | 224 |
| Томская область | 1046 | 275 | 181 | 56 | 56 |
Таблица V.5. Оценка степени риска территории на основе трёх показателей
В целом предварительный анализ состояния территорий в показателях устойчивого развития в сочетании с показателями территориальных рисков показывает, что регионы Сибири движутся в антиустойчивом направлении с предпосылками элементов катастроф.
Математическое моделирование развития может быть выполнено на основе системы обыкновенных дифференциальных уравнений первого порядка, каждая из которых имеет вид
\[\frac{dx_{i} }{dt} =A_{i} -B_{i},~~~~~~~~~(V.19)\]
где $x_{i}$ — фазовая переменная, а $A_{i}$ и $B_{i}$ — скорости увеличения и уменьшения этой переменной, вызванные социально-экономическими процессами и природопользованием.
Величина риска $\textit{R}$ определяется выражением:
\[R = PY,~~~~~~~~~~(V.20)\]
где $\textit{P}$ — вероятность неблагоприятного события и $\textit{Y}$ — величина ожидаемого ущерба. Таким образом, размерность $\textit{R}$ определяется размерностью фазовой переменной, делённой на время, а сам риск $\textit{R}$ со знаком минус должен быть включён в выражение (V.19) для соответствующей фазовой переменной. Ущерб от реализации рисков может быть материальным, финансовым, экологическим и социальным.
Анализ ситуации в Красноярском крае показывает, что динамика его развития антиустойчива с предпосылками катастроф. Это проявляется в частности в уменьшении площади пахотных земель, их плодородия и сборе зерна, в утрате продовольственной безопасности. Таким образом, главный принцип устойчивости развития нарушен.
При выполнении этапа 2013 г. были получены также следующие результаты:
- разработаны общие концепции и модели антропогенных рисков, включая модель оценки территориального риска в показателях опасности и уязвимости, статистическую модель оценки территориального риска;
- созданы алгоритмы и разработана технология картографирования рисков с использованием геоинформационных систем;
- построены карты территориальных рисков для Красноярского края, Кемеровской и Иркутской областей, Республики Саха (Якутия).
Данные методические разработки и практическая апробация позволили приступить к оценкам интегральных рисков отдельных территорий в отраслевом разрезе для критически важных объектов и территорий активного промышленного освоения:
- выполнена общая оценка опасностей для критически важных объектов (радиационно-опасные, химически опасные, взрыво-пожароопасные, гидродинамически опасные) и дана характеристика природных источников опасности;
- разработана общая схема анализа интегрального риска для критически важных объектов и территорий; выполнены расчеты территориальных рисков месторождений нефтегазодобычи Красноярского края с оценкой индексов уязвимости, живучести и защищенности, рисков загрязнения почвы, воды и деградации растительности для Ванкорского, Юрубчено-Тахомского и Куюмбинского месторождений.
Основные публикации:
- Левкевич В. Е. Устойчивое развитие и природно-техногенная безопасность Белоруси и Красноярского края России / Левкевич В. Е., Никитенко П. Г., Москвичев В. В., Шапарев Н. Я., Шокин Ю. И.
Право и экономика. — Минск, 2013. — 171 с. - Андрианова А. В.
Динамика развития енисейского зообентоса в нижнем бъефе Красноярской ГЭС // Вестник ТГУ. Биология, 2013. — № 1(21). — С. 74-88.
(Отделы Вычислительной физики, Прикладной информатики)
| К началу | |