| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2012 год
Программы фундаментальных исследований Сибирского отделения РАН
- III.19. Общая механика, динамика космических тел, транспортных средств и управляемых аппаратов, биомеханика, механика жидкости, газа и плазмы, неидеальных и многофазных сред, а также механика горения, детонации и взрыва
- IV.29. Системы автоматизации, CALS-технологии, математические модели и методы исследования сложных управляющих систем и процессов
- IV.31. Проблемы создания глобальных и интегрированных информационно-телекоммуникационных систем и сетей. Развитие технологий GRID
- VI.32. Архитектура, системные решения, программное обеспечение и информационная безопасность информационно-вычислительных комплексов и сетей новых поколений. Системное программирование
III.19. Общая механика, динамика космических тел, транспортных средств и управляемых аппаратов, биомеханика, механика жидкости, газа и плазмы, неидеальных и многофазных сред, а также механика горения, детонации и взрыва
Программа III.19.1. Математические проблемы нелинейных моделей движения сложных сред
Координатор программы: академик РАН Л. В. Овсянников
Проект «Моделирование движения жидких сред с поверхностями раздела»№ гос. регистрации 01201056403
Научный руководитель проекта: д.ф.-м.н., профессор В. К. Андреев
Блок 1. Исследование движения и устойчивости в новых моделях конвекции при наличии поверхностей раздела (В. К. Андреев, В. Б. Бекежанова, Ю. В. Гапоненко, И. И. Рыжков).
1. Развитие концентрационно-вибрационной конвекции. Анализируются результаты, полученные в ходе эксперимента SOVICON в течение 50-ой кампании параболических полётов Европейского космического агентства. Исследованы две смешивающиеся жидкости системы вода-изопропанол, взятые в различных концентрациях компонентов, которые были подвергнуты периодическим горизонтальным колебаниям с различной частотой и амплитудой. При этом для определённого набора контрольных параметров возникает локализованное осреднённое течение в окрестности тройной точки: точки контакта между двумя жидкостями и твёрдой вертикальной стенкой. Эта неустойчивость происходит в случае, когда амплитуда и частота колебаний выше критического значения, определяемого уровнем вязкой диссипации в жидкости. Результаты численного моделирования подтверждают наблюдаемую экспериментально неустойчивость.
Экспериментальная установка, на которой выполнялись исследования, обеспечивает уровень вибраций с частотой до 12 Гц и амплитудой 20 мм. Наблюдения фиксировались высокоскоростной записью интерферограмм ячейки с жидкостью, размером $10\times5\times2.4$ мм. Численное моделирование проводилось на основе полных и осреднённых уравнений системы Навье — Стокса в приближении Обербека — Буссинеска.
На рис. III.1 представлены результаты эксперимента, где наблюдаются три характерные структуры течения: 1 — трёхвихревое течение при слабых вибрационных воздействиях, 2 — четырёхвихревая структрура квазиравновесного состояния и 3 — трёхвихревая структура с потерей устойчивости переходной зоны между жидкостями.

Рис. III.1. Результаты эксперимента для уровня вибраций: 1 — A = 20 мм, f = 1 Гц; 2 — A = 15 мм, f = 3 Гц; 3 — A = 20 мм, f = 3 Гц
При этом в связи с существенным размытием переходной зоны при начальном заполнении ячейки наблюдаемый эффект неустойчивости является ослабленным за счёт снижения градиента концентрации.
На рис. III.2 показаны результаты эксперимента и численного моделирования, представленные в виде градиентов показателя преломления. Такое сравнение вызвано тем, что результаты эксперимента проблематично преобразовать в форму распределения концентрации в связи с большими градиентами плотности в областях, примыкающим к зонам, где формируется неустойчивость. Тем не менее представленные результаты демонстрируют качественное сходство в структуре течения и динамике его развития.

Рис. III.2. Результаты эксперимента (слева) и численного моделирования при А = 15 мм, f = 3 Гц
Полученные результаты показывают, что наблюдаемая в эксперименте неустойчивость существенно зависит в своей интенсивности от начального распределения компонентов примеси, а также уровней вибрационного воздействия.
2. Численное моделирование конвекции в жидком мосте, обдуваемом потоком газа, в условиях невесомости. В этом пункте представлены результаты численного моделирования термокапиллярной конвекции (конвекция Марангони) в жидком мосте с числом Прандтля, равным Pr = 68 (силиконовое масло), а также выполнен анализ тепловых потоков через границу раздела между жидкостью и газом. Геометрия рассмотренной физической задачи соответствует цилиндрическому жидкому мосту с недеформируемой границей, который окружен концентрическим каналом газа в условиях отсутствия гравитации. Течение газа в канале может быть сонаправленным движению жидкости, вызванным конвекцией Марангони, либо противоположным. При этом воздействие потока газа на жидкость имеет два основных фактора: касательные напряжения вдоль границы раздела и теплообмен. В общем случае охлаждение свободной границы усиливает течение, в то время как нагрев приводит к обратному эффекту. Однако эта тенденция может не выполняться в том случае, если воздействие касательных напряжений и термокапиллярных эффектов является сопоставимым. Полученные результаты показывают, что в случае, вдува газа со стороны холодной границы наблюдается значительное увеличение теплового потока через свободную границу по сравнению со случаем, когда газ вдувается со стороны горячей стенки жидкого моста.
На рис. III.3 представлены результаты расчета течения для $\textit{$\Delta$T} = 5$ K, $\textit{U${}_{gas}$} = -1$ м/с. Течение газа совпадает с направлением термокапиллярной конвекции, что приводит к усилению течения в жидкости и смещению центра вихря к холодной стенке. Кроме того, происходит нагрев свободной границы за счёт тепла, приносимого со стороны горячего стержня, что приводит к уменьшению тепловых потоков через границу раздела сред.
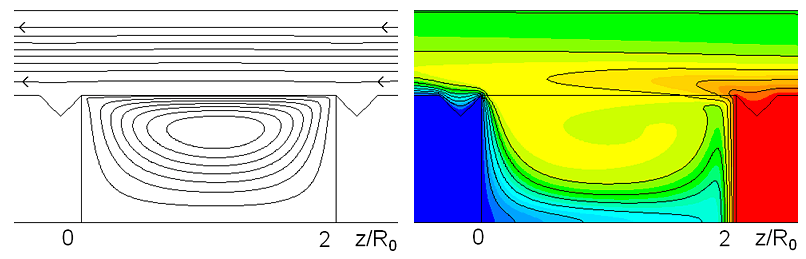
Рис. III.3. Изолинии функции тока и распределение температуры для случая, когда поток газа совпадает с конвекцией Марангони
На рис. III.4 приведены результаты для противоположного случая, когда поток газа направлен со стороны холодного стержня при $\textit{$\Delta$T}$ = 5 K, $\textit{U${}_{gas}$ }$= +1 м/с. При таких параметрах воздействие касательных напряжений со стороны потока газа и термокапиллярной конвекции является сопоставимым по величине, что приводит к сепарации в распределении осевой скорости вдоль свободной границы и формированию двухвихревой структуры течения в жидкости. При этом вихрь возле холодной стенки жидкого моста формируется за счет касательных напряжений, в то время как вихрь возле горячей стенки сформирован за счет термокапиллярной конвекции.
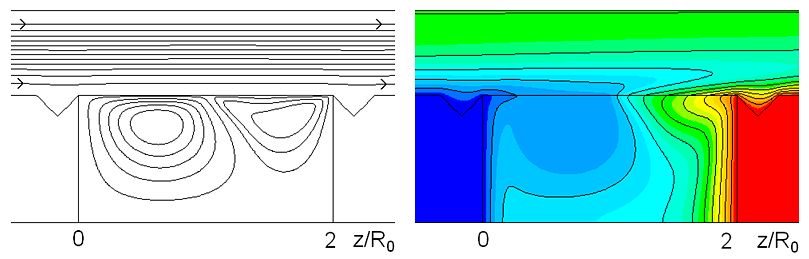
Рис. III.4. Изолинии функции тока и распределение температуры для случая, когда поток газа противоположен конвекции Марангони
На рис. III.5 представлена зависимость осреднённого потока тепла через границу раздела для различных скоростей и температур вдуваемого газа. Видно, что интенсивность теплообмена нарастает в случаях, когда отсутствуют тепловые потери на твёрдых стержнях. При этом наиболее сильный эффект наблюдается в случае вдува холодного газа.
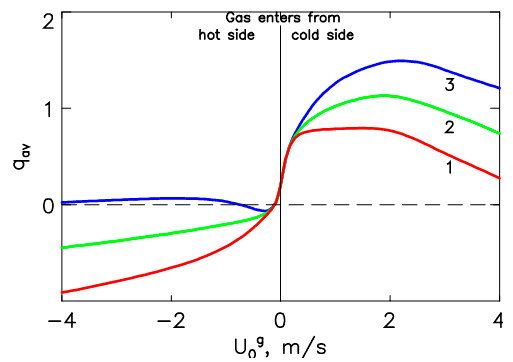
Рис. III.5. Зависимость теплового потока через границу раздела $\textit{q${}_{av}$}$ от скорости газа $\textit{U${}_{gas}$}$ для различных температур вдуваемого газа (1 — $\textit{T${}_{g}$}$ = $\textit{T${}_{hot}$}$, 2 — $\textit{T${}_{g}$}$ = $\textit{T${}_{mean}$}$, 3 — $\textit{T${}_{g}$}$ = $\textit{T${}_{cold}$}$). $\textit{$\Delta$T}$ = 10 K
3. Режимы конвективных течений в вертикальном цилиндре и их устойчивость. Изучена задача о конвективном течении вязкой теплопроводной жидкости в вертикальном цилиндре при наличии объёмных источников тепла. Определена структура возможных режимов течений в зависимости от параметра. Исследована эволюция волновой моды с изменением числа Прандтля. При малых числах Прандтля колебательные моды затухают, а при умеренных и больших нарастают, что приводит к появлению нового типа неустойчивости, связанного с нарастанием в потоке тепловых возмущений.
В рамках модели Обербека — Буссинеска при следующих предположениях:
а) уравнение состояния жидкости принимается в виде $\rho =\rho _{0} [1-\alpha (\theta -\theta _{0} )^{2} ]$;
б) в уравнениях свободной конвекции учтены объёмные источники тепла: в уравнение энергии добавлена общая энергетическая функция теплового источника $F_{w} =\sigma \kappa R_{b} \exp (-\kappa z)$, описывающая проникновение солнечной радиации в жидкую среду,
Построено точное решение, содержащее независимый параметр $a_{1}$ и описывающее стационарное течение жидкости в вертикальном цилиндре
\[u=(u,v,w),\, \, \, u=u_{1} (z)r,\, \, \, v=0,\, \, \, w=w(z),\, \, \, \, \, \, \theta =\theta (z),\, \, \, \, p=q(z)+\frac{a_{1} }{2} r^{2}.\]
Исходная задача разделяется на последовательно решаемые задачи для функций $u_{1} $, $w$, $p$, $\theta $. Краевая задача для функции $u_{1} $ сводится к операторному уравнению $u_{1} =Au_{1} $ с сильно нелинейным оператором $A$. Показано, что $A$ удовлетворяет теореме Шаудера в замкнутом шаре $\bar{S}(0,r_{0} )$ пространства $C[0,1]$, откуда и следует разрешимость операторного уравнения. Получена оценка независимого параметра $a$ в этом шаре. В области реальных значений физических параметров задачи $|a|\, \le \, 0.153$. Предложена итерационная процедура, позволяющая найти три класса решений в зависимости от значений параметра $a$.
Для исследования устойчивости полученных классов течений рассмотрены малые нормальные возмущения скорости, температуры и давления. Выделена критическая тепловая колебательная мода, которая приводит к нарастанию в потоке тепловых волн. В области коротких волн обнаружен другой механизм неустойчивости, при котором кризис связан с нарастанием гидродинамических возмущений (рис. III.6). При положительных значениях параметра происходит перестройка нейтральных кривых: ветви кривых соединяются через замкнутую петлю, при этом оба механизма неустойчивости имеют место. Картина вторичных режимов течений, возникающих при гидродинамическом механизме потери неустойчивости, представлена на рис. III.7.
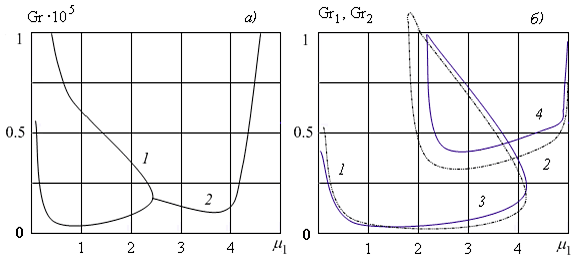
Рис. III.6. Нейтральные кривые $Gr(\mu _{1} )$: а — $a^{1} =-7.341\cdot 10^{-6} $; б — 1,2 — $a^{2} =9.12\cdot 10^{-7} $, $Gr_{1} =Gr\cdot 10^{5} $; 3,4 — $a^{3} =12.0168$, $Gr_{2} =Gr\cdot 10^{6} $
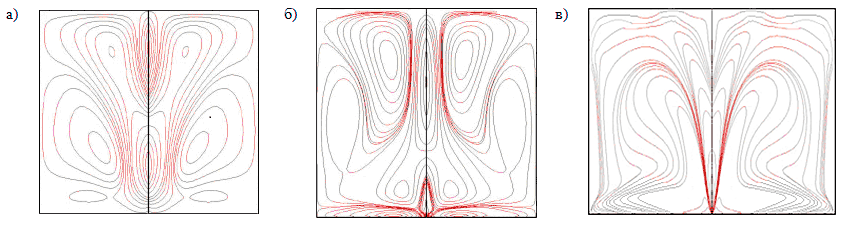
Рис. III.7. Линии тока вторичных режимов при $R=140$м, $Gr=8.5\cdot 10^{5} $: а) — $a^{1} =-7.341\cdot 10^{-6} $; б) — $a^{2} =9.12\cdot 10^{-7} $; в) — $a^{3} =12.0168$
Блок 2. Построение точных решений уравнений движения сложных сред (В. К. Андреев, И. В. Степанова, Е. Н. Лемешкова).
Для двумерной модели термодиффузии
\[{\rho _{0} \frac{du}{dt} ={\rm div}\prod {\rm +}\rho _{0} Fg,\, \, \, \, \, \, \, \, \, \, \, \, \, {\rm div\; }u=0,}\]
\[{\frac{dT}{dt} ={\rm div}(\chi \nabla T),\, \, \, \, \, \, \, \, \, \frac{dC}{dt} ={\rm div(}D\nabla C+D^{T} \nabla T{\rm ),}}\]
где $\prod _{ij} =-p\delta _{ij} +2\rho _{0} \nu (\partial u_{i} /\partial x_{j} +\partial u_{j} /\partial x_{i} )\, $ — тензор напряжений; $d/dt=\partial /\partial t+u_{j} \partial /\partial x_{j} $ обозначает полную производную по времени $t$; по повторяющимся индексам $i,\, \, j=1,2$ предполагается суммирование; $x=(x_{1}, \, \, x_{2} )$ — вектор координат; $u=(u_{1}, \, \, u_{2} )$ — вектор скорости жидкости; $p$ — давление; $g=(0,g)$ — вектор ускорения внешних сил; $\rho _{0} $ — плотность жидкости при средних значениях температуры и концентрации; $T$ и $C$ — отклонение температуры и концентрации от средних постоянных значений; $\nu (T,C)\, \,, $ $\chi (T,C)$, $D(T,C)$, $D^{T} (T,C)$ — коэффициенты вязкости, температуропроводности, диффузии и термодиффузии соответственно; неотрицательная функция $F(T,C)$ определяет силу плавучести; на подалгебре $\left\langle \partial _{t}, \, \, \partial _{x_{1} } +\lambda \partial _{p} \right\rangle $ построены инвариантные решения для различных представлений коэффициентов переноса и силы плавучести:
1) при постоянных значениях коэффициентов переноса получено решение, обобщающее течение Пуазейля на случай движения под действием произвольной силы тяжести;
2) если коэффициенты переноса и сила плавучести заданы соотношениями
\[\nu =\nu _{*} e^{3mT}, \, \, \, \chi =\chi _{*} e^{3mT}, \, \, \, D=D_{*} e^{3mT}, \, \, \, \, D^{T} =e^{3mT} (kT(D_{*} -\chi _{*} )+D_{*}^{T} ),\, \, \, \, \, F=-\frac{s}{g} T+F_{*},\]
где $\nu _{*}, \, \chi _{*}, \, D_{*}, \, \, \, D_{*}^{T} $ — произвольные ненулевые постоянные;
3) если коэффициенты вязкости, температуропроводности, диффузии и термодиффузии и сила плавучести имеют вид
\[\nu =\nu _{*} T^{3m}, \, \, \, \chi =\chi _{*} T^{3m}, \, \, \, D=D_{*} T^{3m}, \, \, \, \, D^{T} =T^{3m-1} [k(D_{*} -\chi _{*} )+D_{*}^{T} ],\, \, \, \, \, F=-\frac{s}{g} \ln T+F_{*}.\]
Полученные решения описывают однонаправленные течения в слоях и могут быть использованы для построения более простых математических моделей, а также для тестирования численных методов.
Блок 3. Редукция уравнений подмоделей и их групповой анализ (О. В. Капцов, Ю. В. Шанько, А. В. Шмидт).
Изучалась проблема Гурса — классификации гиперболических нелинейных уравнений, обладающих двумя нетривиальными инвариантами характеристик. Получен алгоритм нахождения инвариантов характеристик. На основе данного алгоритма, реализованного в системе REDUCE, произведена проверка инвариантов характеристик двух уравнений Лэне.
Показано, что одно из них обладает инвариантами второго и третьего порядков. Наличие такого уравнения показывает, что проблема Гурса остается открытой и результаты работ Жибера и Соколова являются неполными. Компьютерные расчеты демонстрируют, что инварианты характеристик второго уравнения Лэне, приведенные в их работе, указаны неверно.
Выполнены исследования динамики безымпульсного турбулентного следа в пассивно стратифицированной среде. Осуществлено сопоставление приближенного аналитического решения задачи о дальнем безымпульсном турбулентном следе в пассивно стратифицированной среде с численным решением, основанным на непосредственном интегрировании уравнений математической модели.
Предложен аналитический подход, позволяющий повысить точность расчетов трехмерной модели дальнего турбулентного следа за самодвижущимся телом в пассивно стратифицированной среде. На рис. III.8 приводится сопоставление осевых значений кинетической энергии турбулентности в дальнем безымпульсном турбулентном следе за телом вращения с экспериментальными данными и результатами численных расчетов других авторов.
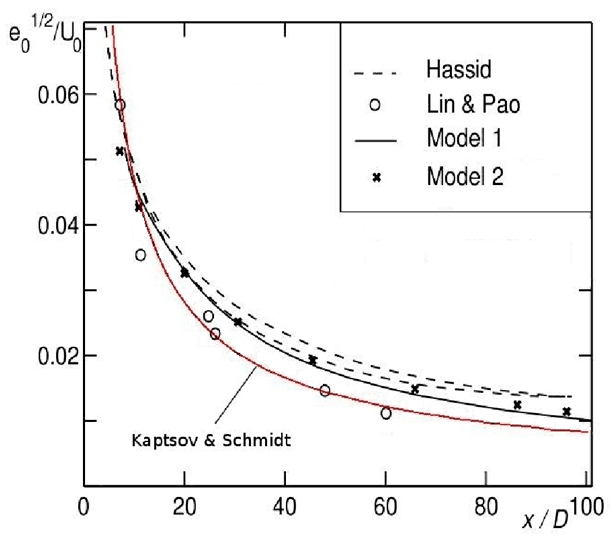
Рис. III.8. Осевые значения кинетической энергии турбулентности в дальнем следе за телом вращения
Дано определение обобщенных функционально-инвариантных (ОФИ) решений класса N для двумерного уравнения распространения звука в неподвижной неоднородной среде. Для данного уравнения выписаны необходимые условия существования таких решений, а также доказано, что они могут быть только классов 1 или 2. Выписаны соотношения на функции скорости звука и плотности, при выполнении которых существуют ОФИ решения класса 2. Показано, как в этом случае можно строить соответствующие точные решения исходного уравнения.
Все полученные результаты являются новыми. Они могут быть использованы для построения решений моделей механики сплошной среды.
Блок 4. Оценка влияния внутренних волн на динамику вертикальных распределений температуры воды в озере Шира, сравнение результатов расчетов с наблюдениями. Выполнить оценку потока СО2 между бореальными лесами и атмосферой в различных регионах на различных временных интервалах (В. М. Белолипецкий, Л. А. Компаниец, С. Н. Генова, П. В. Белолипецкий, Т. В. Якубайлик).
Проведены измерения скоростей течений в озере Шира в летний период. В результате анализа выполненных натурных измерений скоростей течений в озере Шира обнаружены колебания вертикальной компоненты скорости течения, что характерно для внутренних волн в стратифицированном водоеме. Наличие внутренних волн подтверждает анализ изотерм на период с 28.06.2011 по 29.06.2011 (рис. III.9).
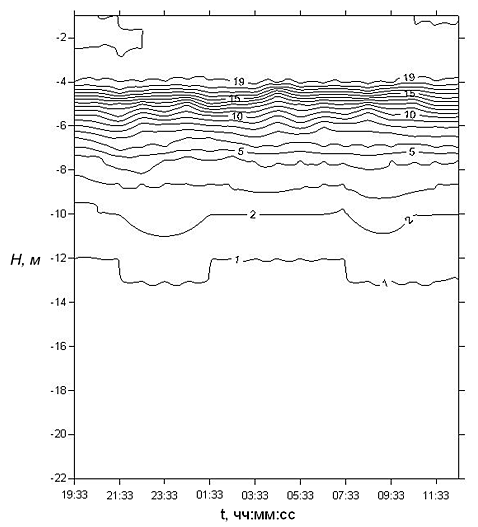
Рис. III.9. Изотермы для периода с 28.06.2011 по 29.06.2011
Анализ распределения плотности и частоты Брента-Вяйсяля (рис. 3) показывает, что можно ожидать появления внутренних волн в диапазоне 4−12 м, что соответствует рис. III.9.
Проведено моделирование вертикальной структуры течения в озере Шира при наличии внутренних волн в рамках следующих предположений: а) в уравнениях движения опускаются нелинейные конвективные члены и отсутствуют члены, отвечающие за турбулентную вязкость; b) выполняется условие гидростатики; c) в уравнении для температуры опускаются диффузионные члены, но остается конвекция в вертикальном направлении; отсутствуют тепловые потоки; d) жидкость стратифицирована только по вертикали; e) дно бассейна ровное; f) распределение плотности по глубине имеет «трехслойную» структуру; g) на поверхности ставится условие «твердой крышки».
В рамках этой модели основная активность внутренних колебаний проявляется в области глубины от 4 до 12 м.
Предлагается упрощенный способ оценки влияния внутренних волн на вертикальные распределения температуры и солености воды в соленом озере. Предполагается, что вертикальные распределения температуры, солености и плотности воды в озере вычислены по одномерной модели.
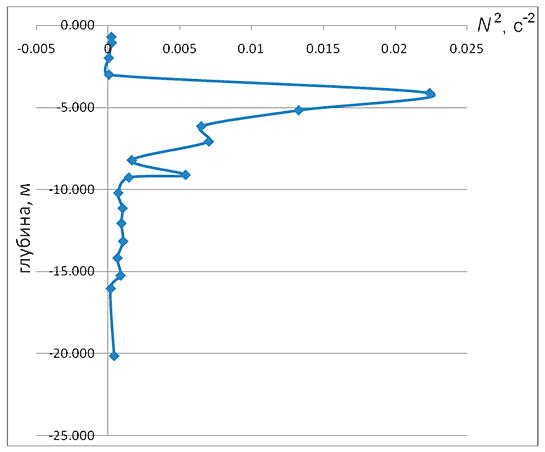
Рис. III.10. Квадрат частоты Брента-Вяйсяля в соответствии с формулой Буссинеска
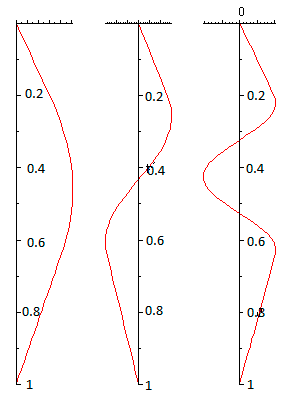
Рис. III.11. Первые 3 моды вертикальной составляющей скорости
Для оценки влияния внутренних волн на вертикальную структуру стратифицированного водоема рассматривается следующая упрощенная постановка задачи. Стратифицированный водоем схематизируется трехслойной жидкостью (рис. III.12). В верхнем слое воды, прилегающем к свободной поверхности ($-d_{1} \le z\le 0$), из-за перемешивания плотность воды равна постоянному значению, в пикноклине ($0\le z\le d_{2} $) плотность изменяется линейно по глубине, в придонном слое ($d_{2} \le z\le d_{1} +d_{3} $) плотность меняется мало, $\rho \approx const$. $d_{1}, \; d_{2}, \; d_{3} $ — толщины соответствующих слоев, $d_{1} +d_{2} +d_{3} =H$ — глубина водоема. Плотность воды предполагается непрерывной на границах раздела слоев $z=0$ и $z=d_{2} $ (рис. III.12).
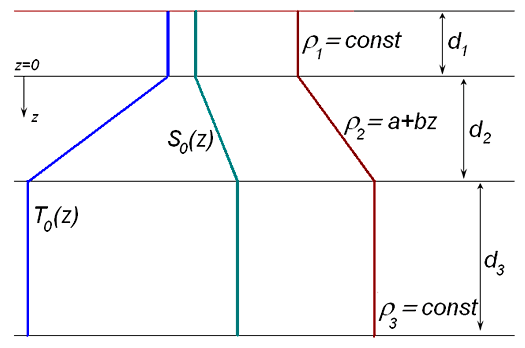
Рис. III.12. Трехслойная схема водоема
$N^{2} =\frac{g}{\rho _{00} } \, \frac{d\, \rho }{d\, z} $ — частота Вяйсяля — Брента ($\rho _{00} $ — характерная плотность). Для рассматриваемой схемы $N_{1} =0$, $N_{2} =const$, $N_{3} =0$.
Волновые процессы в жидкости изучаются на основе линеаризованных уравнений гидродинамики. Используются приближение Буссинеска (изменения плотности воды учитываются только в силе тяжести), приближение гидростатики и приближение «твердой крышки» (вертикальная компонента скорости течения воды на свободной поверхности $z=-d_{1} $ равна нулю).
Основное уравнение для внутренних волн выводится из двумерных в вертикальной плоскости линейных уравнений гидродинамики несжимаемой невязкой жидкости:
\[\frac{\partial ^{2} }{\partial \, t^{2} } \, (\frac{\partial ^{2} \, \psi }{\partial \, z^{2} } )+N^{2} \, \frac{\partial ^{2} \, \psi }{\partial \, x^{2} } =0,\]
здесь $\textit{x}$, $\textit{z}$ — прямоугольные координаты, ось z направлена вниз, $\textit{t}$ — время, $\psi \, (x,\, z)$ — функция тока.
Граничные условия для трехслойной жидкости (рис. III.12). На водной поверхности (в приближении «твердой крышки») и на дне вертикальная компонента скорости равна нулю.
На границах раздела слоев выполняются кинематическое (в линейном приближении равенство вертикальных скоростей) и динамическое (равенство полных давлений по обе стороны от границы) граничные условия.
Решение основного уравнения, удовлетворяющее граничным условиям, ищется в виде распространяющейся в горизонтальном направлении гармонической волны:
\[\psi \, (t,\, x,\, z)=\varphi \, (z)\cdot \cos \, (kx-\omega \, t),\]
$\omega $ — частота, $\lambda =\frac{2\pi }{k} $ — длина волны.
Для определения функции $\varphi (z)$получается уравнение:
\[\frac{d^{2} \varphi }{d\, z^{2} } +k^{2} \frac{N^{2} }{\omega ^{2} } \varphi =0.\]
Так как $\textit{N${}_{1}$}$=0, $N_{2} =\sqrt{\frac{g\, \Delta \, \rho }{\rho _{00} d_{2} } } $, $\textit{N${}_{3}$}$=0, $\Delta \, \rho =\rho _{3} -\rho _{1} $, то решения этого уравнения имеют вид:
\[\varphi _{\, 1} (z)=a_{1} +b_{1} \, z~~~~~~при~~~~~~-d_{1} \le z\le 0,\]
\[\varphi _{\, 2} (z)=a_{2} \cdot \sin \frac{N_{2} }{c} z+b_{2} \cdot \cos \frac{N_{2} }{c} z~~~~~~при~~~~~~0\le z\le d_{2},\]
\[\varphi _{\, 3} (z)=a_{3} +b_{3} \, z~~~~~~при~~~~~~-d_{1} \le z\le 0,\]
\noindent здесь $c=\frac{\omega }{k} $ — скорость распространения внутренних волн. Вертикальная компонента скорости определяется по формуле
\[w=k\cdot \varphi \, (z)\cdot \sin (k{\kern 1pt} x-\omega \, t).\]
Для определения констант $a_{\, i}, \; b_{{\kern 1pt} i} \; (i=1,2,3)$ получается однородная система уравнений, которая имеет нетривиальное решение, если ее определитель равен нулю. Отсюда следует дисперсионное соотношение для внутренних волн:
\[tg\frac{N_{2} d_{2} }{c} =\frac{(d_{1} +d_{3} )\, AN_{2} }{d_{1} {\kern 1pt} d_{3} N_{2}^{2} -c^{2} }.\]
Дисперсионное уравнение имеет бесконечную последовательность $A_{n} $ возможных значений с, расположенных в порядке убывания и соответствующих различным модам, $c_{n}^{\bullet } \lt c_{n} \lt c_{n-1}^{\bullet }, \; {\rm \; \; }n=1,2,3...$, где $c_{0}^{\bullet } =\sqrt{d_{1} \cdot d_{3} } \cdot N_{2} $, $c_{n}^{\bullet } =\frac{N_{2} d_{2} }{0.5\, \pi +(n-1)\, \pi } \; (n\ge 1)$. Наибольший корень уравнения находится в интервале $(c_{1}^{\bullet }, \, c_{0}^{\bullet } )$.
Предлагается следующий алгоритм для оценки влияния внутренних волн на вертикальную структуру стратифицированного озера:
1. На первом этапе решается одномерная (в вертикальном направлении) задача без учета внутренних волн. Определяется динамика вертикальных распределений температуры, солености и плотности воды.
2. На втором этапе для конкретных суток рассчитанные вертикальные распределения температуры, солености, плотности воды схематизируются трехслойной жидкостью (рис. 5). Затем определяются колебания температуры и солености в пикноклине в течение суток из решения уравнений:
\[\frac{\partial \, T}{\partial \, t} +w\, \frac{\partial \, T}{\partial \, z} =0, \frac{\partial \, S}{\partial \, t} +w\, \frac{\partial \, S}{\partial \, z} =0,\]
где вертикальная составляющая вектора скорости определяется по формуле $w=-k\cdot \varphi \, (z)\cdot \sin (\omega \, t)$.
Выполнены расчеты вертикальных распределений температуры, солености и плотности воды в озере Шира по одномерной модели без учета внутренних волн. На рис. III.13 приведены результаты расчетов и данные натурных измерений. Одномерная модель без учета внутренних волн позволяет с удовлетворительной точностью определить положения термоклина, халоклина и пикноклина, а также значения температуры и солености в поверхностном и придонном слоях.
Колебания температуры и солености воды в пикноклине можно оценить с использованием упрощенной одномерной модели внутренних волн. На рис. III.14 приведены результаты натурных измерений вертикальных распределений температуры воды в озере Шира и примеры расчетов для суперпозиции двух мод внутренних волн с периодом 5 часов. Рассчитанные амплитуды колебаний температуры согласуются с измеренными.
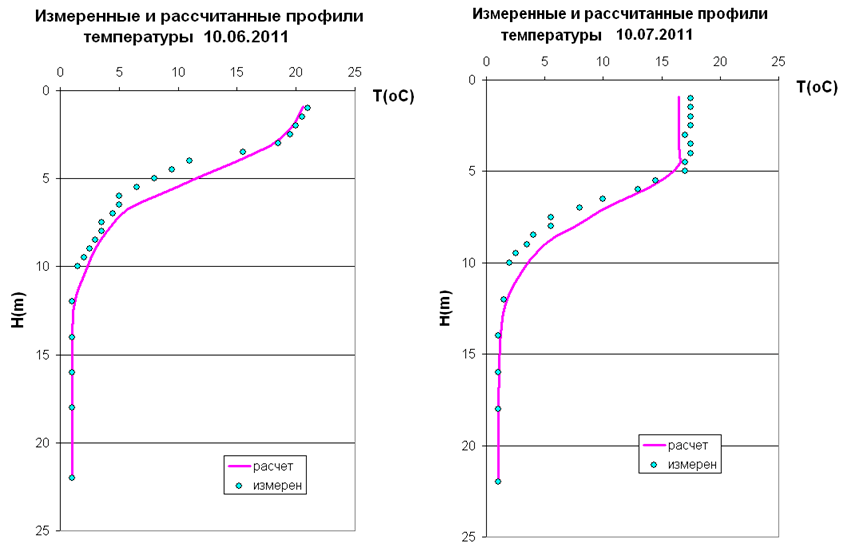
Рис. III.13. Расчетные и измеренные профили температуры воды в оз. Шира
С помощью разработанного способа оценки потока углерода вблизи поверхности Земли с использованием точечной модели и измеренных на вышке вертикальных распределений концентраций углекислого газа выполнены оценки потока СО2 между бореальными лесами и атмосферой для известных данных, полученных на вышке Зотино (в Красноярском крае). Показано, что суммарный годовой поток отрицательный, т.е. преобладает поглощение углерода наземными экосистемами.
Сезонные изменения вертикальных распределений температуры и солености воды необходимо учитывать при математическом моделировании динамики компонентов водной экосистемы.
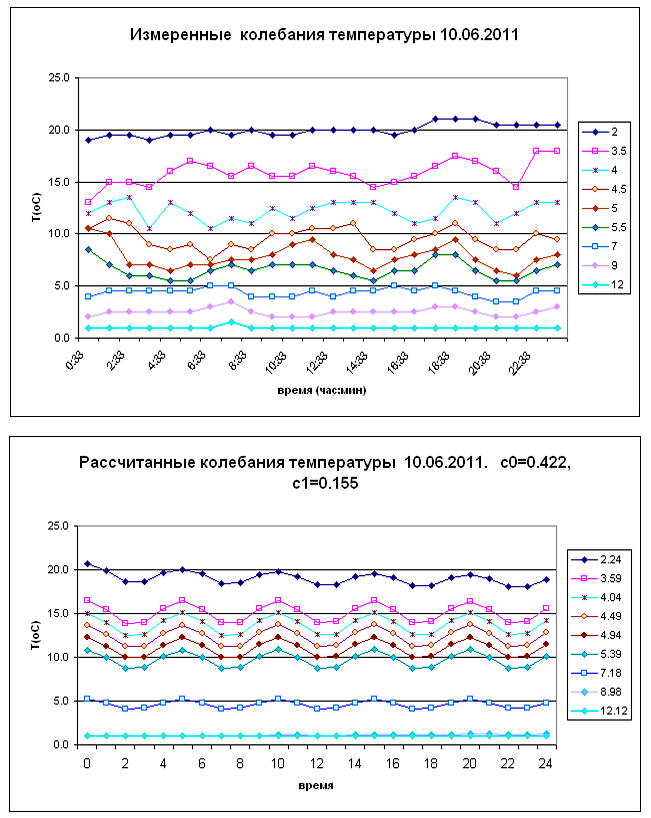
Рис. III.14. Измеренные и рассчитанные колебания температуры воды в озере Шира на различных глубинах
Основные публикации:
К блоку 1:
- Gaponenko Yu., Shevtsova V.
Heat Transfer Through the Interface and Flow Regimes in Liquid Bridge Subjected to Co-Axial Gas Flow // Microgravity Science and Technology, 2012. — V. 24. — P. 297–306 . - Gaponenko Y., Mialdun A., Shevtsova V.
Interfacial shear stress in gas-liquid flow in annuli // J. Multi Phase Flow, 2012. — V. 39. — P. 205–215 . - Андреев В. К., Собачкина Н. Л.
Движение бинарной смеси в плоских и цилиндрических областях. — Красноярск: Редакционно-издательский отдел СФУ, 2012. — 188 с. - Андреев В. К., Бекежанова В. Б.
Устойчивость неизотермических жидкостей // ПМТФ. — Новосибирск, 2012 (в печати). - Бекежанова В. Б.
О режимах конвективных течений вязкой жидкости в вертикальном цилиндре и их устойчивости // Тр. XVI Междунар. конф. «Современные проблемы механики сплошной среды». — Ростов-на Дону: ЮФУ, 2012. — С. 31-35. - Андреев В. К., Бекежанова В. Б.
Об одном решении уравнений свободной конвекции при наличии объемных источников тепла // ПММ,. 2012 (в печати).
К блоку 2:
- Андреев В. К., Stepanova I. V.
Equation for convection in binary mixture: symmetry analysis and exact solutions // Abstr. book of 23rd Int. Congr. of Theoretical and Applied Mechanics. — Beijing, China, 2012. — P. 117. - Лемешкова Е. Н.
Стационарное течение трех жидкостей в плоском слое под действием термокапиллярных сил и перепада давления // J. of Siberian Federal University.- Mathematics and Physics, 2012. — № 5 (1). — P. 91-96.
К блоку 3:
- Капцов О. В.
О проблеме классификации Гурса // Программирование, 2012. — Т. 38. — № 2. — С. 68-71. - Капцов О. В., Черных Г. Г., Фомина А. В., Шмидт А. В.
Автомодельное вырождение турбулентного следа за буксируемым телом в пассивно стратифицированной среде // ПМТФ, 2012. — № 5. С. 47-54. - Kaptsov O. V., Schmidt A. V.
Application of the B-Determining Equations Method to One Problem of Free Turbulence // Symmetry, Integrability and Geometry: Methods and Appliations, 2012. — V. 8, Iss. 73. — 10 p.
К блоку 4:
- Компаниец Л. А., Якубайлик Т. В., Гаврилова Л. В. и др.
Аналитические решения для задач стационарного ветрового движения жидкости. Красноярск: СФУ, 2012. — 120 с. - Володько О. С., Компаниец Л. А., Якубайлик Т. В.
Анализ характеристик озера Шира на основе натурных наблюдений // Вестник БГУ, 2012. — Вып. 9. — С. 167–176 . - Компаниец Л. А., Якубайлик Т. В., Гаврилова Л. В.
Теоретические и экспериментальные исследования скоростного режима озера Шира в летний период. Препринт № 12-3. — Красноярск: ИВМ СО РАН, 2012. — 47 с.
(Отделы Дифференциальных уравнений механики, Вычислительных моделей в гидрофизике)
| К началу | |