| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2012 год
Программы фундаментальных исследований Сибирского отделения РАН
- III.19. Общая механика, динамика космических тел, транспортных средств и управляемых аппаратов, биомеханика, механика жидкости, газа и плазмы, неидеальных и многофазных сред, а также механика горения, детонации и взрыва
- IV.29. Системы автоматизации, CALS-технологии, математические модели и методы исследования сложных управляющих систем и процессов
- IV.31. Проблемы создания глобальных и интегрированных информационно-телекоммуникационных систем и сетей. Развитие технологий GRID
- VI.32. Архитектура, системные решения, программное обеспечение и информационная безопасность информационно-вычислительных комплексов и сетей новых поколений. Системное программирование
VI.32. Архитектура, системные решения, программное обеспечение и информационная безопасность информационно-вычислительных комплексов и сетей новых поколений. Системное программирование
Программа IV.32.1. Архитектура, информационная безопасность, системные решения и программное обеспечение информационно-вычислительных систем новых поколений
Координаторы программы: член-корреспондент РАН В. Г. Хорошевский, член-корреспондент РАН В. В. Шайдуров
Проект IV.32.1.4. «Анализ сложных математических моделей на суперкомпьютерах с параллельной архитектурой»№ гос. регистрации 01201056402
Научный руководитель проекта: д.ф.-м.н., профессор В. М. Садовский
Блок 1. Численное исследование динамических процессов в средах с микроструктурой (В. М. Садовский, О. В. Садовская, М. П. Варыгина).
В рамках теории малых упругопластических деформаций однородной и изотропной пористой среды построены поля перемещений и напряжений вокруг расширяющихся полостей сферической и цилиндрической формы. Переход среды в пластическое состояние моделируется с помощью условия текучести Треска — Сен-Венана. Изменение пористости описывается на основе оригинальной математической модели, учитывающей повышение жесткости материала в момент схлопывания пор. Показано, что на упругой стадии деформирования пористость не меняется. С ростом давления в окрестности полости образуется зона пластического уплотнения, в части которой поры схлопываются. В случае цилиндрической симметрии сначала появляется зона неполной пластичности, затем ее часть, прилегающая к полости, переходит в состояние полной пластичности. Получены инженерные формулы для вычисления критических давлений предельного упругого состояния и предельного состояния среды с раскрытыми порами, а также формулы для определения радиусов поверхностей раздела зон пластичности и уплотнения.
Блок 2. Численный анализ элементов конструкций из композитных материалов (А. Д. Матвеев, С. Ф. Пятаев, И. В. Киреев).
Для анализа деформации трехмерных неоднородных тел и композитных конструкций разработана процедура построения смешанных дискретных конечноэлементных моделей малой размерности, которые способны учитывать сложную структуру, сложную форму области и порождают решения, отличающиеся от решений базовых моделей на заданную величину. Суть смешанных дискретных моделей состоит в том, что в окрестности крепления конструкции или участка границы сложной формы используется мелкое разбиение, состоящее из известных односеточных конечных элементов, остальная часть конструкции представляется крупным разбиением, которое состоит из многосеточных конечных элементов. Размерности смешанных дискретных моделей меньше размерности базовой модели и поэтому реализация метода конечных элементов требует значительно меньше оперативной памяти ЭВМ и временных затрат. Предложен новый алгоритм определения эффективных модулей упругости для плоских неоднородных тел и тонких композитных пластин регулярной структуры на основе микроподхода, который удобно реализуется на ЭВМ с помощью конечноэлементных алгоритмов.
Для исследования предельного термоупругого поведения линейно-армированных композиционных материалов в рамках структурного подхода разработана модель ансамбля высокопрочных волокон, внедренных в низкомодульную матрицу. Геометрическая структура этого ансамбля в трансверсальной плоскости (плоскости, ортогональной направлению волокон) состоит из объединения периодической системы неоднородных ячеек, моделирующих волокна, окруженных матрицей (рис. III.34).
Рис. III.34. Геометрическая структура ансамбля в трансверсальной плоскости
Термосиловое нагружение порождает однородное макронапряженное состояние и неоднородное микронапряженное состояние, зависящее от осевой координаты, направленной вдоль волокон. Получены расчетные предельные значения нагрузок при поперечном и продольном нагружениях. Расчеты проводились для полимерного композиционного материала и металлического композита. Проведено сравнение результатов с экспериментальными и известными теоретическими данными, которое показало хорошее совпадение. В обоих случаях расчетные данные отклонялись от экспериментальных в сторону уменьшения. Это можно объяснить тем, что построенная вычислительная модель описывает зарождение разрушения, а экспериментальные данные отражают полное разрушение композитной системы.
Блок 3. Моделирование и численный анализ распространения поверхностных волн в больших акваториях с учетом влияния внешних геодинамических факторов (К. В. Симонов, Е. Д. Карепова, Е. В. Дементьева).
Выполнено тестирование быстрых алгоритмов на гибридных вычислительных архитектурах по моделированию распространения цунами от сильнейших цунамигенных землетрясений 20
Рассмотрены различные аспекты математического и численного моделирования приливных течений и поверхностных волн в больших открытых акваториях. Предложен, исследован и реализован итерационный алгоритм восстановления по данным наблюдений неизвестной граничной функции, описывающей влияние океана через открытую границу расчетной области, состоящий из последовательного решения прямой и сопряженной задач, а также уравнения для уточнения граничной функции. Для решения прямой и сопряженной задач используется метод конечных элементов. Проведено исследование эффективности нескольких параллельных реализаций алгоритма численного решения начально-краевой задачи для уравнений мелкой воды, выполненных с помощью библиотеки MPI для языка Cи. Проведены сравнительные результаты ускорения вычислений в зависимости от количества процессов, способа реализации коммуникаций, способа декомпозиции вычислительной области и архитектуры кластерной системы.
Блок 4. Параллельная реализация генетического алгоритма оптимизации в гидрологических моделях трансформации стока (Е. Д. Карепова, магистрант ИМ СФУ М. А. Сухотин).
Для восстановления параметров классической модели трансформации речного стока по данным наблюдений применен генетический алгоритм оптимизации и выполнена его параллельная реализация для высокопроизводительных вычислительных систем. В изучаемой модели производится вычисление расхода потока несжимаемой жидкости в выходном створе открытого русла при заданном расходе потока во входном створе и известной передаточной функции. Основными характеристиками, влияющими на решение задачи, являются средняя скорость потока и параметр продольного рассеивания. Для решения оптимизационной задачи применялись генетические алгоритмы. Во-первых, генетические алгоритмы обладают хорошим потенциальным параллелизмом. Во-вторых, используя только значения целевой функции, они не требуют никакой дополнительной информации (о возможных оврагах, локальных минимумах и проч.), а также информации о гладкости оптимизируемой функции.
Для тестового численного эксперимента были выбраны данные по расходу воды в створе Иваньковской ГЭС (входной створ модели). В качестве замыкающего створа был выбран створ в 9,1 км ниже по течению. На рис. III.36 отображены график расходов во входном створе специального попуска ГЭС, график наблюденных расходов в замыкающем створе и график расходов, рассчитанных по модели.
Были также оценены основные характеристики параллельной реализации генетического алгоритма оптимизации с помощью библиотек MPI и OpenMP для языка Си (рис. 2). Расчеты проводились на кластере ИМ СФУ.
Ступенчатое поведение ускорения параллельного алгоритма объясняется его насыщаемостью. Этого можно избежать, перераспределив число поколений и количество особей в популяции, однако алгоритм слабо масштабируем. Было также показано, что совместное использование технологий распараллеливания задач OpenMP и MPI для SMP-узлового кластера не дает существенных преимуществ, поскольку время, затрачиваемое на обмены сравнимо со временем, затрачиваемым на синхронизацию нитей и мало до момента насыщения.
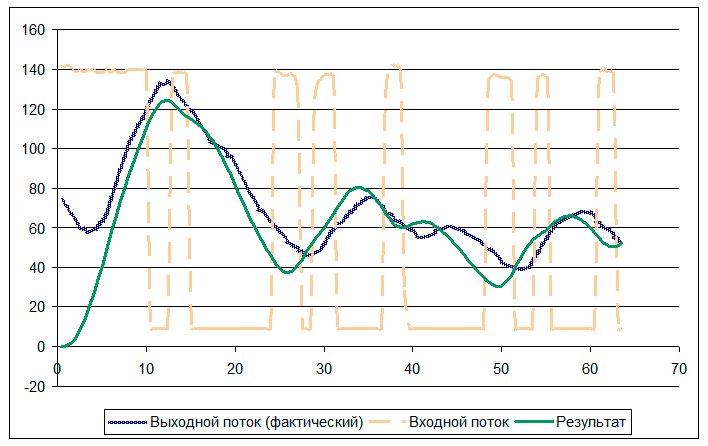
Рис. III.35. Численный эксперимент по данным наблюдений на Иваньковской ГЭС. По оси абсцисс отложено время в часах от начала специального попуска, по оси ординат — расход в м3/с
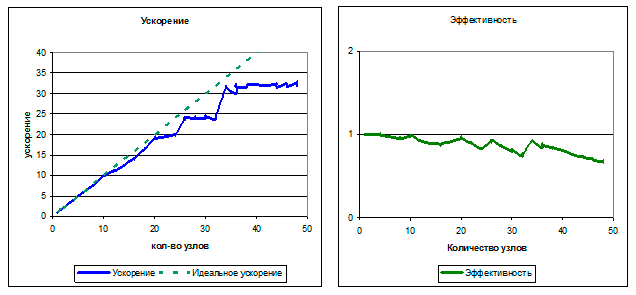
Рис. III.36. Ускорение (слева) и эффективность (справа), полученные при расчетах на кластере ИМ СФУ
Блок 5. Разработка параллельных методов для численного решения систем обыкновенных дифференциальных уравнений (Е. А. Новиков, А. Н. Рогалев).
Создана динамическая гибридная модель электрической сети, учитывающая возможные критические ситуации. Построены методы второго и третьего порядка точности для решения гибридных задач и проведены их тестовые испытания на многопроцессорной вычислительной системе кластерной архитектуры. Разработаны новые аддитивные методы решения жестких задач для систем обыкновенных дифференциальных уравнений, в которых допускаются различные способы аппроксимации матрицы Якоби.
Разработаны эффективные алгоритмы и программы для вычисления гарантированных границ множеств решений обыкновенных дифференциальных уравнений с неточно заданными данными на высокопроизводительных ЭВМ. В практических задачах управление ведется в условиях априорной неопределенности относительно внешних воздействий, либо относительно текущего состояния объекта. При этом состояние объекта измеряется с некоторыми погрешностями. Внешние воздействия заранее неизвестны и могут измеряться в ходе процесса с некоторой ошибкой. При построении управления предполагаются известными лишь некоторые общие характеристики возмущений и погрешностей измерения, а их конкретные реализации непредсказуемы.
Необходимо обеспечить определенное качество процессов при управлении в условиях неопределенности. Для этого существуют два подхода: вероятностный и гарантированный (минимаксный), каждый из которых имеет свои преимущества. При вероятностном подходе предполагается, что участвующие в задаче факторы неопределенности обладают свойством статистической устойчивости и представляют собой случайные величины или случайные функции с известными вероятностными характеристиками. По ним могут быть найдены вероятностные характеристики исследуемых управляемых процессов, которые в ряде случаев могут служить показателями качества управления (например, показатель точности — величина среднеквадратической ошибки). Однако вероятностный подход к задачам определения и коррекции движения иногда приводит к выводам, не соответствующим реальным условиям решаемых задач. Это в первую очередь относится к оценке точности получаемых результатов и выбору стратегии решения задачи, обеспечивающей максимальную точность.
Если необходимо обеспечить качество процесса в каждом отдельном случае, то приходится ориентироваться на самое неблагоприятное (экстремальное) сочетание параметров неопределенности. В этом случае для описания всех фазовых состояний динамических систем используется детерминированный подход, оценивающий все фазовые состояния в условиях неточных измерений.
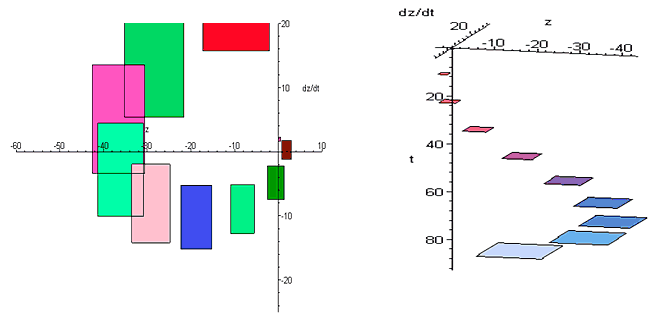
Рис. III.37. Границы включений областей допустимых отклонений под влиянием быстрых изменений скорости бокового ветра (при выборе области допустимых начальных состояний объекта управляющее воздействие стремится к увеличению размеров области, а возмущение стремится уменьшить их)
Гарантированные методы, основанные на символьном представлении формул решений, применены в двух типичных задачах динамики полета, при решении которых необходимо учитывать влияние многих реально существующих возмущений на движение летательного аппарата. Одна из таких задач — задача анализа процесса автоматической посадки самолета — в первую очередь сводится к оценке возможных значений параметров траекторного и углового движения самолета в момент касания шасси взлетно-посадочной полосы. Этот этап можно расценить как наиболее ответственный в смысле выполнения ограничений, наложенных на параметры движения. Вторая задача заключается в оценке областей всех возможных фазовых состояний самолета (множеств достижимости) при движении по горизонтальной плоскости при условии, что текущее состояние системы измеряется неточно, но с известными ограничениями на ошибку измерений.
Основные публикации:
- Sadovskaya O., Sadovskii V.
Mathematical Modeling in Mechanics of Granular Materials. Series: Advanced Structured Materials [Электронный ресурс] / Springer: Heidelberg — New York — Dordrecht — London, 2012. — V. 21. — 390 p. ISSN: 1869–844 1 (electronic). ISBN: 978-3-642–290 53-4 (eBook). Режим доступа: http://link.springer.com/book/10.1007/978-3-642–290 53-4. - Novikov E. A.
The variable structure algorithm based on L-stable and explicit methods // Russ. J. Numer. Anal. Math. Model, 2012. — V. 27, (3). — P. 243–259 . - Пятаев С. Ф.
Структурное моделирование критерия прочности периодических композитов при сложном температурно-силовом нагружении // Дальневосточный математический журнал, 2012. — Т. 12. — № 2. — С. 262–273 . - Матвеев А. Д.
Анализ прочности с учетом характера распределения эквивалентных напряжений в конструкциях // Известия АлтГУ, 2012. — Т. 73. — № 1-1. — С. 81-85. - Karepova E., Dementyeva E.
The numerical solution of the inverse problem for shallow water models // 5-th Conf. on Numerical Analisis and Applications. — Bulgaria, Rousse: University of Rousse Publ, 2012. — P. 23-24.
(Отделы Вычислительной математики, Вычислительной механики деформируемых сред, Служба средств телекоммуникаций и вычислительной техники)
| К началу | |