| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2012 год
Программы фундаментальных исследований Сибирского отделения РАН
- III.19. Общая механика, динамика космических тел, транспортных средств и управляемых аппаратов, биомеханика, механика жидкости, газа и плазмы, неидеальных и многофазных сред, а также механика горения, детонации и взрыва
- IV.29. Системы автоматизации, CALS-технологии, математические модели и методы исследования сложных управляющих систем и процессов
- IV.31. Проблемы создания глобальных и интегрированных информационно-телекоммуникационных систем и сетей. Развитие технологий GRID
- VI.32. Архитектура, системные решения, программное обеспечение и информационная безопасность информационно-вычислительных комплексов и сетей новых поколений. Системное программирование
IV.29. Системы автоматизации, CALS-технологии, математические модели и методы исследования сложных управляющих систем и процессов
Программа IV.29.1. Теоретические основы и методы информационных и вычислительных технологий проектирования и принятия решений
Координаторы программы: академик РАН Ю. И. Шокин, член-корреспондент РАН В. В. Шайдуров
Проект IV.29.1.2 «Информационно-вычислительные технологии для анализа и проектирования сложных систем в ближнем космосе»№ гос. регистрации 01201056404
Научный руководитель проекта: член-корреспондент РАН В. В. Шайдуров
Блок 1. Создание программно-вычислительного комплекса на основе технологии многокомпонентного программирования, позволяющего вести конструкторскую проработку тепловых режимов приборных блоков различного назначения (В. А. Деревянко, Е. Н. Васильев, А. В. Макуха, С. В. Кукушкин, Д. А. Нестеров, В. В. Деревянко, М. И. Корхова, Д. А. Пустынский, О. Д. Горохов, Д. П. Емельянов).
Разработан программно-вычислительный комплекс (ПВК) «Panel Emulator» для расчетов теплового режима приборного блока космического аппарата (КА) негерметичного исполнения. Расчетная часть и интерфейс ПВК разделены и реализованы в разных программных компонентах, связанных между собой с помощью XML-схемы. При моделировании тепловых режимов учитываются циклограммы включения приборов и нагревателей, динамика изменения внешних радиационных потоков при движении КА по орбите. ПВК позволяет задавать геометрию приборной сотовой панели с учетом отверстий и выступов. ПВК предоставляет конструктору удобный графический интерфейс, с помощью которого можно задавать конфигурацию приборов и элементов терморегулирования на поверхностях сотовой панели. В процессе проведения вычислений динамика изменения температурных полей отображается в цвете (рис. III.15). Также предусмотрена возможность отслеживания изменения температуры в заданных точках поверхности и индикации перегрева приборов. ПВК разработан по заданию ОАО «ИСС» и внедрен в проектном отделе.
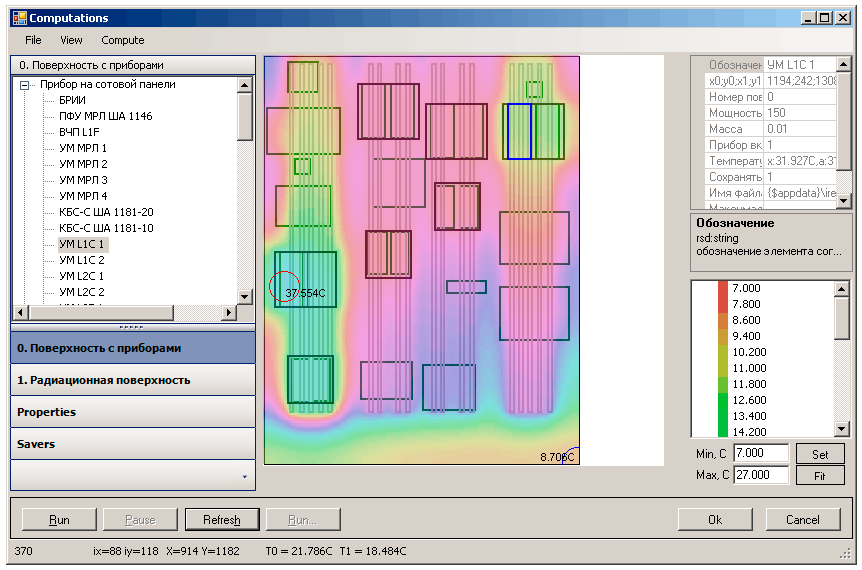
Рис. III.15. Окно с параметрами приборного блока и цветовым отображением температурного поля поверхности панели
Блок 2. Создание стационарной модели увлечения геомагнитного поля в хвост магнитосферы Земли за счет движения плазменного слоя (Н. В. Еркаев, В. В. Денисенко).
Выполнены аналитико-численные исследования особенностей течения солнечного ветра в области магнитосферного хвоста. Показано, что динамическое взаимодействие магнитного поля с движущейся плазмой приводит к возникновению ускоренных потоков плазмы и генерации медленных магнитозвуковых волн, распространяющихся от экватора к высоким широтам. Показано, что распределение скорости солнечного ветра в этой области существенно неоднородно и зависит от интенсивности межпланетного магнитного поля. Результаты данных исследований опубликованы в журнале Geophysical research Letters (2012).
Внутри магнитосферного хвоста исключительно важную роль играют процессы магнитного пересоединения, осуществляющие быстрое преобразование магнитной энергии в кинетическую энергию плазмы и тепло. В связи с этим выполнялись работы по моделированию диффузионной области магнитного пересоединения в плазменном слое, где происходит генерация электрического поля и ускорение частиц. Статья на эту тему опубликована в журнале Journal of Geophysical Research (2012). Выполнены численные исследования условий развития неустойчивости Кельвина-Гельмольца при обтекании солнечным ветром планет. Результаты опубликованы в журналах Physics of Plasmas (2012) и Journal of Geophysical Research (2012).
Блок 3. Моделирование систем формирования высокоупорядоченных холодных частиц с целью приложения в нанотехнологиях.
1. Предложен новый тип оптического тянущего пучка (ОТП) для манипулирования частицами: бихроматический оптический тянущий пучок. Построена математическая модель воздействия такого пучка на частицы (И. В. Краснов).
ОТП (optical tractor beam) — световой пучок, создающий отрицательное световое давление на микро(нано)частицы или атомы. ОТП способен захватывать отдалённые частицы и транспортировать их на макроскопические расстояния в направлении противоположном (!) направлению потока излучения, т.е. «притягивать» частицы непосредственно к источнику света. Первые теоретические предложения ОТП (J. Chen, J. Ng, Z. Lin, C. T. Chan, Nat. Photon. 5 (9) (2011) 531; S. Sukhov, A. Dogariu, Phys. Rev. Lett. 107 (20) (2011) 203602 Novitsky, C.-W. Qiu, H. Wang, Phys. Rev. Lett. 107 (20) (2011) 203601) основаны на использовании анизотропии в рассеянии световых пучков микрочастицами определённых типов.
В настоящей работе предложен ОТП нового типа — бихроматический оптический тянущий пучок (БОТП), предназначенный для оптического манипулирования атомами (ионами) и другими подобными частицами, которые имеют узкие оптические резонансы. Действие БОТП основано на управлении силами резонансного вынужденного светового давления (а не силами рассеяния как в упомянутых первых работах по ОТП) в комбинированном оптическом пучке: специальной суперпозиции параксиальных (коллимированных) Гауссовских и косинус-Гауссовских световых пучков, содержащих компоненты с сильно различающимися частотами.
Математическая модель для теоретического обоснования предложенной схемы БОТП включает в себя явные аналитические представления оптических полей — решений параксильного волнового уравнения; уравнения квазиклассической теории резонансного светового давления (оптические уравнения Блоха для матрицы плотности для резонансных частиц, выражения для светоиндурованных сил в дипольном приближении); Ньютоновские уравнения движения частиц. Анализ этой модели и численное моделирование действия БОТП на частицы позволил получить следующие наиболее важные результаты.
Установлено, что эффект отрицательного светового давления (собственно эффект тянущего оптического пучка) возникает только при определённых фазовых соотношениях между компонентами БОТП и соотношениях между интенсивностями формирующих его пучков.
Показано, что cветоиндуцированная сила в поле действия БОТП сложным нелинейным образом зависит от параметров поля и координат частицы в фазовом пространстве. Для этой силы получены явные приближённые аналитические выражения.
Продемонстрировано, что помимо продольной силы отрицательного светового давления, обеспечивающей «притяжение» частиц к источнику излучения, на них действует отрицательная радиальная сила (Рис. III.16) и поперечная нелинейная сила трения, обеспечивающие эффективное притяжение частиц в приосевую область БОТП и устойчивость их движения.
Найдены соответствующие условия устойчивости траекторий частиц.
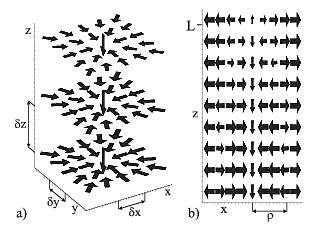
Рис. III.16. Векторное поле светоиндуцированных сил для медленных частиц (более длинные стрелки соответствуют большим силам). (а) 3D поле светоиндуцированных сил в малой окрестности оси бихроматического оптического тянущего пучка (БОТП). (b) поле светоиндуцированных сил в плоскости $xz$. Масштабы для поперечных координат $x,y$ и аксиальной координаты $z$ существенно различны: $\delta x/\delta z,\delta y/\delta z\sim 10^{-2} $, $\delta z$$\approx 4D$, $\rho \approx 0.2D$, $L\approx 14D$ ($D$ и $L$-радиус и «дальность» действия бихроматического оптического тянущего пучка. БОТП формируется в плоскости $z=0$
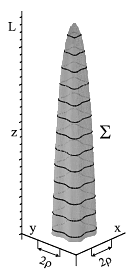
Рис. III.17. Типичный вид границы $\Sigma$ аттрактора БОТП. Все конкретные параметры БОТП такие же как на Рис. III.16
Показано, что область притяжения (аттрактор) БОТП в пространстве координат имеет вытянутую «иглоподобную» форму (Рис. III.17) и резко сужается при удалении от источника излучения (плоскости $z=0$, на которой формируется БОТП) на характерное расстояние $\sim L$, определяемое предельной дистанцией сохранения поперечной пространственной структуры косинус-Гауссовского оптического пучка. Величина $L$ имеет смысл «дальности» действия БОТП, значительно превышает его радиус $D$ и увеличивается $\propto I^{1/4} $ при увеличении интенсивности $I$ сильной компоненты поля, формирующего БОТП.
Продемонстрировано, что типичная картина (Рис. III. 18) движения частиц, в начальный момент времени находящихся в области действия (притяжения) БОТП, имеет две характерные стадии: быстрого притяжения частиц к оси БОТП (стадия захвата частиц световым пучком) и последующего движения в приосевой области БОТП по направлению к источнику излучения: плоскости $z=0$ на Рис.3. Причем аксиальное движение частиц может сопровождаться значительным ускорением. Оценки показывают, что БОТП способен эффективно воздействовать на ансамбли частиц с начальными продольными температурами более 50 K при интенсивностях излучения $I\sim 3 кВт/см^{2}$.
2. Рассмотрено прохождение резонансного излучения через расширяющуюся сферическую газовую среду, имеющую градиент скорости (Н. Я. Шапарев).
Показано, что поглощение излучения в среде уменьшается, что связано с допплеровским смещением частоты поглощения, вызванным расширением среды. Определяющим фактором в данном процессе является соотношение между оптической толщиной стационарной среды $\tau _{0} $ и величиной $V_{R} /V_{0} $, где $V_{R} $ — скорость расширения границы среды, $V_{0} $ — средняя тепловая скорость. При $V_{R} /V_{0} \gg \tau _{0}$ наступает просветление среды.
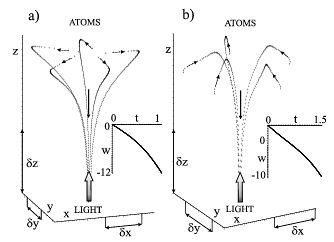
Рис. III.18. Типичные траектории частиц в поле действия бихроматического оптического тянущего пучка (БОТП). Ось $z$-направление распространения света (толстые стрелки), источник света расположен в плоскости $z=0$, тонкие стрелки указывают направления движения частиц. Вставка — зависимость безразмерной аксиальной скорости частиц $W$ от безразмерного времени $t$ (определение $W$ и $t$, начальные условия для скоростей частиц, а также конкретные параметры БОТП для данного рис. приведены в работе [1]). (a) В начальный момент времени частицы «убегают» от оси БОТП в перпендикулярном направлении. (b) В начальный момент времени частицы «убегают» от источника света почти параллельно оси БОТП, т.е. имеют большие положительные начальные скорости и относительно малые поперечные начальные скорости
На рис. III.19 представлены значения вероятности выхода резонансного излучения как функции оптической толщины $\tau _{0}$ при различных значениях $V_{R} /V_{0}$, которая уменьшается с ростом $\tau _{0}$ и увеличивается с ростом $\alpha =V_{R} /V_{0}$. Видно, что при $\alpha \gg \tau _{0}$ (кривая 5) излучение свободно проходит через среду.
На рис. III.20 представлены спектральные характеристики входящего и выходящего излучений. При отсутствии разлёта ($\alpha =0$) спектр выходящего излучения является самообращённым (кривая 1). При $\alpha \ne 0$ контур становится ассиметричным (кривые 2, 3, 4). Красное крыло спектральной линии из-за эффекта Допплера, связанного с разлётом, поглощается слабее, а голубое крыло поглощается сильнее. При $\alpha \gg \tau _{0} $ среда просветляется, излучение проходит через среду, слабо поглощаясь (кривая 5), сохраняя свою начальную форму (кривая +).
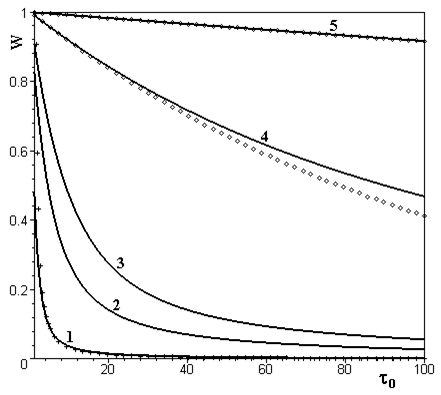
Рис. III.19. Вероятность выхода резонансного излучения. Кривые 1, 2, 3, 4, 5 соответствуют выражению при $\alpha =0;\, 1;\, 10;\, 100;\, 1000$
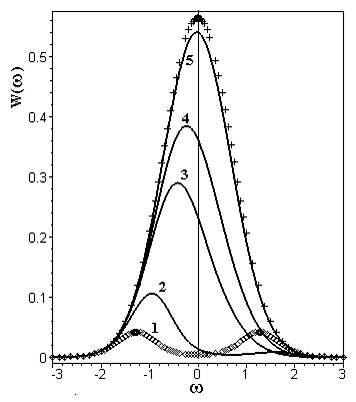
Рис. III.20. Форма контура резонансного излучения. + — нормированный контур входного излучения $W(\omega )=e^{-\omega ^{2} } /\sqrt{\pi } $. 1, 2, 3, 4, 5 — контур линии выходящего излучения при $\tau _{0} =5$ и $\alpha =0;\, 1;\, 5;\, 10;\, 100$
3. С использованием приближений «ближайшего соседа» и ячеек Вигнера-Зейтца для ультрахолодной плазмы, создаваемой с помощью фотоионизации охлажденных атомов, были получены аналитические оценки значений параметров неидеальности электронной и ионной подсистем, устанавливающиеся в результате их корреляционного и рекомбинационного нагрева (А. П. Гаврилюк).
Сравнение с экспериментальными данными показало их адекватность. Кроме того, на основе этих исследований была обнаружена возможность создания электрон-ионной плазмы с сильно неидеальной электронной подсистемой путем возбуждения атомов в определенные ридберговские состояния.
Построена математическая модель разнополярного заряжения двух сталкивающихся разноразмерных металлических наночастиц, обусловленного туннельным переносом электронов. На основе метода броуновской динамики показано, что в процессе коагуляции энергия парных взаимодействий металлических наночастиц разного размера может возрастать за счет электростатической добавки, возникающей из-за взаимного разнополярного заряжения частиц. Причиной такого заряжения может быть туннельный перенос электронов, протекающий в момент столкновения разноразмерных частиц. Этот перенос обусловлен зависимостью работы выхода электронов от размера частиц. На примере бимодальных наноколлоидов серебра показано, что взаимное разнополярное заряжение разноразмерных частиц может приводить к ускорению коагуляции полидисперсных коллоидных систем на порядок величины по сравнению с монодисперсными системами, в которых данный эффект не проявляется.
Блок 4. Численное моделирование сверхзвуковых течений вязкого теплопроводного газа (В. В. Шайдуров, Г. И. Щепановская, М. В. Якубович).
Рассмотрены сверхзвуковые течения вязкого теплопроводного газа. Использована математическая модель на основе полных нестационарных уравнений Навье-Стокса для двумерного случая. Дискретизация по пространству осуществляется методом конечных элементов. Метод траекторий применяется при аппроксимации по времени, впервые для всей системы уравнений Навье-Стокса. Исследована дискретная модель. Использование комбинации метода траекторий и метода конечных элементов позволяет в десятки раз уменьшить сложность построения дискретных аналогов на каждом временном слое. В итоге реализован экономичный алгоритм на высокопроизводительных вычислительных системах.
Полученный пакет программ позволяет определить решение в широком диапазоне чисел Маха и Рейнольдса. На рис. III.21−III.22 представлено сверхзвуковое течение вязкого теплопроводного газа в плоском канале с прямоугольным уступом. Показано распределение продольной составляющей скорости и распределение плотности в канале с уступом. Числа Маха и Рейнольдса равны соответственно M = 2 и Re = 2x1000 на момент времени t = 20,0.

Рис. III.21. Распределение продольной составляющей скорости

Рис. III.22. Распределение плотности в канале
На рис. III.22 по центру канала наблюдается система скачков уплотнения, которым соответствует распределение скорости на рис. III.21. За уступом формируется зона нулевых и отрицательных значений скорости, протяжённость которой увеличивается с ростом числа Маха. В угловой точке уступа происходит отрыв течения. Картина течения соответствует экспериментальным представлениям.
Основные публикации:
К блоку 2:
- Biernat H. K., Erkaev N. V., Farrugia C. J., Mezentsev A., Torbert R. B.
Accelerated magnetosheath flows caused by IMF draping: Dependence on latitude // Geophys. Res. Lett, 2012. — V. 39. — P. L01103. - Biernat H. K., Divin A. V., Erkaev N. V., Korovinskiy D. B., Lapenta G., Markidis S., Semenov V. S.
Scaling of the inner electron diffusion region in collisionless magnetic reconnection // J. Geophys. Res, 2012. — V. 117. — P. A06217. - Biernat H. K., Erkaev N. V., Moestl U. V., Zellinger M.
2.5D magnetohydrodynamic simulation of the Kelvin-Helmholtz instability around Venus-Comparison of the influence of gravity and density increase // Phys. Plasmas, 2012. — V. 19. — Iss. 2. — P. 022104. - Korovinskiy D., Divin A., Erkaev N., Ivanova V., Ivanov I., Semenov V., Lapenta G., Markidis S., Biernat H., Zellinger M.
MHD modeling of the double-gradient (kink) magnetic instability // J. Geophys. Res., in press, 2012. - Bagenal F., Delamere P. A., Desroche M., Erkaev N. V.
Conditions at the expanded Jovian magnetopause and implications for the solar wind interaction // J. Geophys. Res, 2012. — V. 117. — P. A07202. - Erkaev N. V., Farrugia C. J., Galvin A. B., Harris B., Leitner M., Luhmann J. G., Mostl C., Ogilvie K. W., Osherovich V. A., Simunac K. D.C., Szabo A., Temmer M. B., Torbert R. B., Veronig A. M.
Deep Solar Activity Minimum 2007 — 2009: Solar Wind Properties and Major Effects on the Terrestrial Magnetosphere // Sol. Phys, 2012. — V. 281. — Iss. 1. — P. 461–489 .
К блоку 3:
- Krasnov I. V.
Bichromatic optical tractor beam for resonant atoms // Phys. Lett. A, 2012. — V. 376. — Iss. 42-43. — P. 2743–274 9. - Kosarev N. I., Shaparev N. Ya.
Scattering and absorption of resonant radiation in an expanding sphere // J. Phys. B-At. Mol. Opt. Phys, 2012. — V. 45. — Iss. 16. — P. 165003. - Shaparev N. Ya.
Reduced absorption of resonant radiation in expanding gaseous media // Proceeding of Int. conf. on optoelectronics and microelectronics. — China, Changchun, 2012. — P. 342–345 . - Гаврилюк А. П., Карпов С. В., Семина П. Н.
Роль электронного туннельного эффекта в кинетике коагуляции полидисперсных наноколлоидов металлов // Коллоидный журнал, 2012. — Т. 74. — № 3. — С. 329–336 .
К блоку 4:
- Schepanovskaya G. I., Shaidurov V. V., Yakubovich M. V.
Numerical modelling of supersonic flows in channel // Russ. J. Numer. Anal. Math. Model, 2012. — V. 27, (6). — P. 501–516 . - Щепановская Г. И.
Математическое и численное моделирование течений вязкого теплопроводного газа // Вестник СибГАУ, 2011. — Т. 5. — № 38. — С. 101–106 .
(Отделы Вычислительной математики, Вычислительной физики)
| К началу | |